用 Python 构建高级配对交易策略
作者:老余捞鱼
原创不易,转载请标明出处及原作者。
写在前面的话:
本文阐述通过分析加密货币和传统金融工具之间的相关性和协整性,以及实施 Z-score 方法来生成交易信号,然后介绍如何使用 Python 构建配对交易策略,从而在市场中寻找交易机会。最后还讨论了实际遇到的交易挑战,强调评估策略要考虑风险调整指标。
配对交易作为一种复杂的策略,常常被交易者运用以管理投资组合,而非仅仅聚焦于单个资产。本文将深入探讨这种市场中性策略,其旨在从两种密切相关的金融工具的相对价格变动中获取利润。本文我们还是借助可免费获取的雅虎财经数据展开模拟分析。
这种策略的核心是相信,随着时间的推移,两种资产的价格会保持稳定的价差。因此,无论市场大趋势如何,交易者都能从价格趋同中获利。配对交易的目标是所选资产之间的关系,而不是整体市场方向。
1. 环境配置
要在 Jupyter 环境中设置必要的库,请使用以下命令:
!pip install numpy
!pip install pandas
!pip install yfinance 在 Jupyter Notebook 单元里运行这些命令,便能将指定的库直接安装到环境当中。安装完毕后,我们就能够继续展开分析了。
2. 收集数据
要使用 Yahoo Finance 数据为涉及加密货币的配对交易策略实施数据收集和清理,请遵循以下步骤:
- 插补缺失值:填补数据中的空白,以保持数据的连续性。
- 平滑异常值:应用平滑极端数据点的方法,以避免分析失真。
- 确保时间序列长度一致:尽管加密货币市场存在持续的交易活动,但要对时间序列数据进行标准化,以确保长度一致。
下面是 Python 的实现方法:
crypto_forex_stocks = ['BTC-USD', 'ETH-USD', 'BNB-USD', 'XRP-USD', 'ADA-USD', 'DOGE-USD', 'ETC-USD', 'XLM-USD', 'AAVE-USD', 'EOS-USD', 'XTZ-USD', 'ALGO-USD', 'XMR-USD', 'KCS-USD',
'MKR-USD', 'BSV-USD', 'RUNE-USD', 'DASH-USD', 'KAVA-USD', 'ICX-USD', 'LINA-USD', 'WAXP-USD', 'LSK-USD', 'EWT-USD', 'XCN-USD', 'HIVE-USD', 'FTX-USD', 'RVN-USD', 'SXP-USD', 'BTCB-USD']
bank_stocks = ['JPM', 'BAC', 'WFC', 'C', 'GS', 'MS', 'DB', 'UBS', 'BBVA', 'SAN', 'ING', ' BNPQY', 'HSBC', 'SMFG', 'PNC', 'USB', 'BK', 'STT', 'KEY', 'RF', 'HBAN', 'FITB', 'CFG',
'BLK', 'ALLY', 'MTB', 'NBHC', 'ZION', 'FFIN', 'FHN', 'UBSI', 'WAL', 'PACW', 'SBCF', 'TCBI', 'BOKF', 'PFG', 'GBCI', 'TFC', 'CFR', 'UMBF', 'SPFI', 'FULT', 'ONB', 'INDB', 'IBOC', 'HOMB']
global_indexes = ['^DJI', '^IXIC', '^GSPC', '^FTSE', '^N225', '^HSI', '^AXJO', '^KS11', '^BFX', '^N100',
'^RUT', '^VIX', '^TNX']
START_DATE = '2021-01-01'
END_DATE = '2023-10-31'
universe_tickers = crypto_forex_stocks + bank_stocks + global_indexes
universe_tickers_ts_map = {ticker: load_ticker_ts_df(
ticker, START_DATE, END_DATE) for ticker in universe_tickers}
def sanitize_data(data_map):
TS_DAYS_LENGTH = (pd.to_datetime(END_DATE) -
pd.to_datetime(START_DATE)).days
data_sanitized = {}
date_range = pd.date_range(start=START_DATE, end=END_DATE, freq='D')
for ticker, data in data_map.items():
if data is None or len(data) < (TS_DAYS_LENGTH / 2):
# We cannot handle shorter TSs
continue
if len(data) > TS_DAYS_LENGTH:
# Normalize to have the same length (TS_DAYS_LENGTH)
data = data[-TS_DAYS_LENGTH:]
# Reindex the time series to match the date range and fill in any blanks (Not Numbers)
data = data.reindex(date_range)
data['Adj Close'].replace([np.inf, -np.inf], np.nan, inplace=True)
data['Adj Close'].interpolate(method='linear', inplace=True)
data['Adj Close'].fillna(method='pad', inplace=True)
data['Adj Close'].fillna(method='bfill', inplace=True)
assert not np.any(np.isnan(data['Adj Close'])) and not np.any(
np.isinf(data['Adj Close']))
data_sanitized[ticker] = data
return data_sanitized
# Sample some
uts_sanitized = sanitize_data(universe_tickers_ts_map)
uts_sanitized['JPM'].shape, uts_sanitized['BTC-USD'].shape 日期范围 "变量用 "pd.date_range(start=START_DATE, end=END_DATE, freq='D') "定义,为数据建立所需的时间范围。接下来,我们使用线性插值法填补所有缺失值(NaN 或 Nones),如果线性插值法失败,则使用最近的有效值进行回填。
我们运用断言语句来校验数据的完整性,同时检查随机选取的两个仪器的形状,以确保它们能相匹配。
3. 深入探讨
大家也许还记得 FTX丑闻 吧?伴随这家交易所的倒闭,投资者或许会对加密货币交易所丧失信心,暂且转向传统银行进行金融交易,直至丑闻被淡忘。
为了探究这一假设,我们能够运用相关性分析与协整分析,来判定加密货币市场和传统银行业表现之间的任何模式或者关系。相关性分析会助力我们知晓两个数据集之间的线性关系程度,而协整性分析则会明确它们之间是否存在长期关系,进而提示潜在的配对交易契机。
通过研究这些指标,我们可以评估丑闻是否影响了市场对加密货币和传统银行业的情绪。
4. 相关性和协整性
相关性使用皮尔逊相关系数 Pearson correlation coefficient (r) 来衡量两个变量之间的关系,其范围为-1 到 1。1 表示完全的负线性关系,0 表示没有线性关系,1 表示完全的正线性关系。

而协整则是评估两种资产是否随着时间的推移而联系在一起,表明它们的价差倾向于回归均值。当它们暂时偏离历史关系时,这就为交易创造了机会。协整关系是通过统计检验来评估的,如扩增迪基-富勒 Dickey-Fuller (ADF) 检验,该检验可检查两种资产之间的价差是否静止。如果价差是静态的,则表明这两种资产是协整的,并且具有长期关系。

幸运的是,numpy 和 stats 库提供了简化这些统计测试的函数,使相关性和协整分析的执行变得更加容易。
5. 寻找配对
在交易中,当资产间的价差背离历史均值之际,分析师会借助协整检验来生成买入与卖出信号。当价差回归至长期均衡状态时,此般偏离便会造就获利契机。故而,对这种分析而言,掌控全面的数据极为关键。
下面的代码将检验一系列股票和其他金融工具,以发现任何隐藏的关系。它将检验零假设 (H0),即假设资产之间没有影响或关系。一般来说,如果检验的 p 值 低于 0.02,则拒绝零假设 (H0),表明这对资产之间存在一定程度的协整关系或值得进一步研究的关系。
from statsmodels.tsa.stattools import coint
from itertools import combinations
from statsmodels.tsa.stattools import coint
def find_cointegrated_pairs(tickers_ts_map, p_value_threshold=0.2):
"""
Find cointegrated pairs of stocks based on the Augmented Dickey-Fuller (ADF) test.
Parameters:
- tickers_ts_map (dict): A dictionary where keys are stock tickers and values are time series data.
- p_value_threshold (float): The significance level for cointegration testing.
Returns:
- pvalue_matrix (numpy.ndarray): A matrix of cointegration p-values between stock pairs.
- pairs (list): A list of tuples representing cointegrated stock pairs and their p-values.
"""
tickers = list(tickers_ts_map.keys())
n = len(tickers)
# Extract 'Adj Close' prices into a matrix (each column is a time series)
adj_close_data = np.column_stack(
[tickers_ts_map[ticker]['Adj Close'].values for ticker in tickers])
pvalue_matrix = np.ones((n, n))
# Calculate cointegration p-values for unique pair combinations
for i, j in combinations(range(n), 2):
result = coint(adj_close_data[:, i], adj_close_data[:, j])
pvalue_matrix[i, j] = result[1]
pairs = [(tickers[i], tickers[j], pvalue_matrix[i, j])
for i, j in zip(*np.where(pvalue_matrix < p_value_threshold))]
return pvalue_matrix, pairs
# This section can take up to 5mins
P_VALUE_THRESHOLD = 0.02
pvalues, pairs = find_cointegrated_pairs(
uts_sanitized, p_value_threshold=P_VALUE_THRESHOLD) 将资产间的关系予以可视化,对于人工解读与决策而言至关重要,即便在算法交易中亦是如此。热图能够依据协整检验所得出的 p 值,直观地展现哪些资产属于配对资产。该热图有益于识别具有重要关系的潜在配对,从而为进一步分析以及探寻交易机会提供助力。
5.1 创建和显示热图
import seaborn as sns
plt.figure(figsize=(26, 26))
heatmap = sns.heatmap(pvalues, xticklabels=uts_sanitized.keys(),
yticklabels=uts_sanitized.keys(), cmap='RdYlGn_r',
mask=(pvalues > (P_VALUE_THRESHOLD)),
linecolor='gray', linewidths=0.5)
heatmap.set_xticklabels(heatmap.get_xticklabels(), size=14)
heatmap.set_yticklabels(heatmap.get_yticklabels(), size=14)
plt.show()
为了简化我们的分析,并专注于加密货币之间最紧密的关系,我们可以选择 p 值 最低的前三个货币对。这些货币对表明了最强的协整关系,因此也是潜在的交易机会。我们可以用柱状图来直观地显示这些货币对及其各自的 p 值。下面介绍如何实现这一点:
5.2 抽取前三名,绘制柱形图,直观显示 P 值。
sorted_pairs = sorted(pairs, key=lambda x: x[2], reverse=False)
sorted_pairs = sorted_pairs[0:35]
sorted_pairs_labels, pairs_p_values = zip(
*[(f'{y1} <-> {y2}', p*1000) for y1, y2, p in sorted_pairs])
plt.figure(figsize=(12, 18))
plt.barh(sorted_pairs_labels,
pairs_p_values, color='red')
plt.xlabel('P-Values (1000)', fontsize=8)
plt.ylabel('Pairs', fontsize=6)
plt.title('Cointegration P-Values (in 1000s)', fontsize=20)plt.grid(axis='both', linestyle='--', alpha=0.7)
plt.show()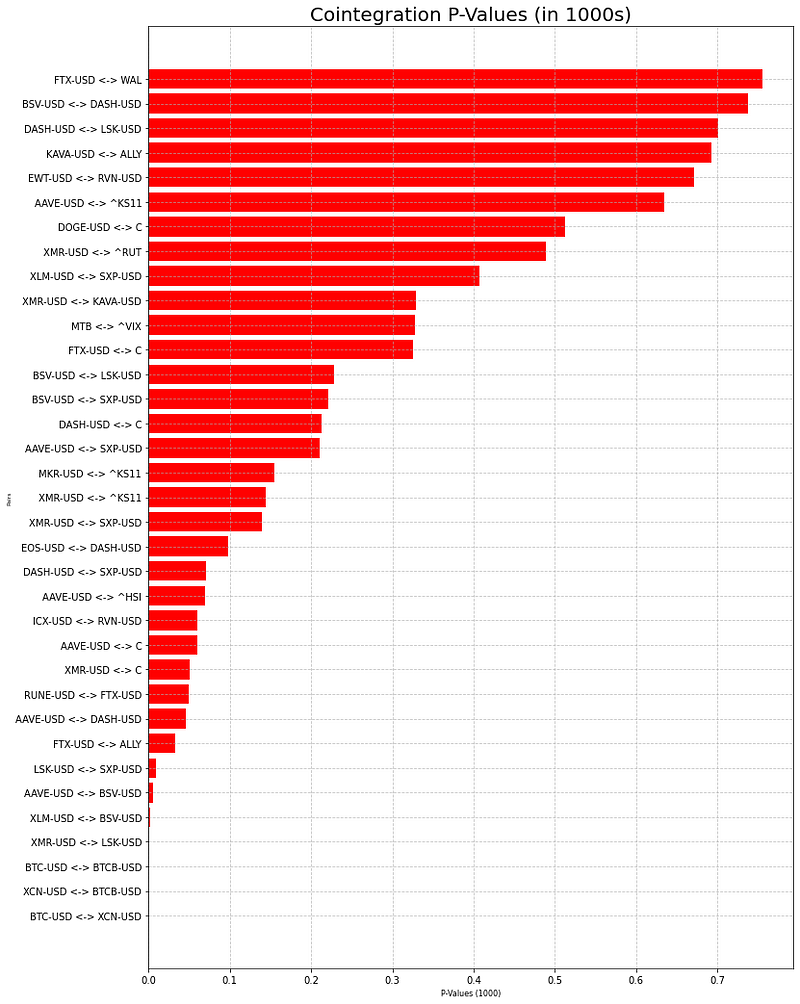
为了将已确定的货币对交易的时间序列数据(花旗集团的 AAVE-USD 交易、花旗集团的 XMR-USD 交易以及 Ally Financial Inc (ALLY) 的 FTX-USD 交易)进行可视化,同时便于对加密货币和股票进行比较,我们将采用 scikit-learn 的 MinMax 缩放功能来对价格进行缩放处理。另外,我们还会运用滚动窗口进行平滑操作,以增强货币对之间固定性的可视程度。
下面是如何实现这一点的方法:
from sklearn.preprocessing import MinMaxScaler
ticker_pairs = [("AAVE-USD", "C"), ("XMR-USD", "C"), ("FTX-USD", "ALLY")]
fig, axs = plt.subplots(3, 1, figsize=(18, 14))
scaler = MinMaxScaler()
for i, (ticker1, ticker2) in enumerate(ticker_pairs):
# Scale the price data for each pair using MIN MAX
scaled_data1 = scaler.fit_transform(
uts_sanitized[ticker1]['Adj Close'].values.reshape(-1, 1))
scaled_data2 = scaler.fit_transform(
uts_sanitized[ticker2]['Adj Close'].values.reshape(-1, 1))
axs[i].plot(scaled_data1, label=f'{ticker1}', color='lightgray', alpha=0.7)
axs[i].plot(scaled_data2, label=f'{ticker2}', color='lightgray', alpha=0.7)
# Apply rolling mean with a window of 15
scaled_data1_smooth = pd.Series(scaled_data1.flatten()).rolling(
window=15, min_periods=1).mean()
scaled_data2_smooth = pd.Series(scaled_data2.flatten()).rolling(
window=15, min_periods=1).mean()
axs[i].plot(scaled_data1_smooth, label=f'{ticker1} SMA', color='red')
axs[i].plot(scaled_data2_smooth, label=f'{ticker2} SMA', color='blue')
axs[i].set_ylabel('*Scaled* Price $', fontsize=12)
axs[i].set_title(f'{ticker1} vs {ticker2}', fontsize=18)
axs[i].legend()
axs[i].set_xticks([])
plt.tight_layout()
plt.show()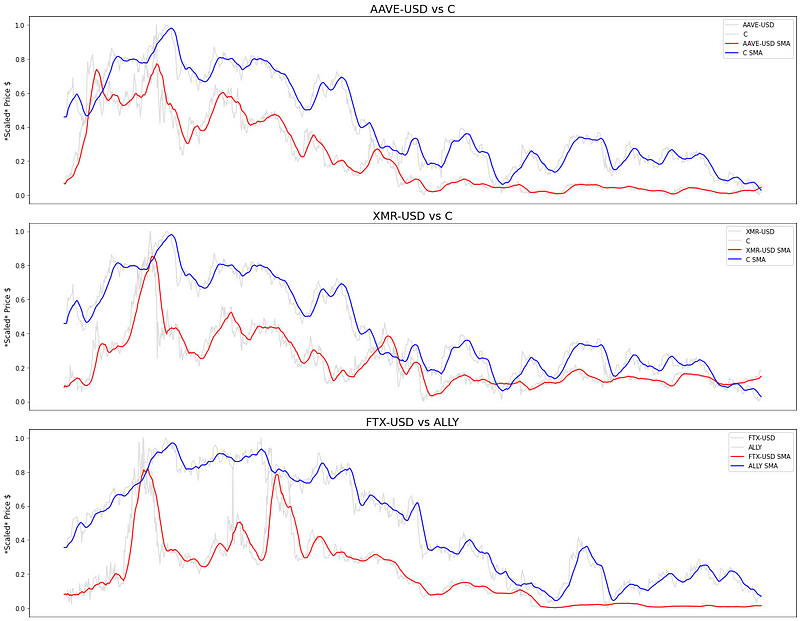
以下是对上述内容的解释:
为了探究 AAVE-USD 和花旗集团之间的潜在交易信号,我们观察到,尽管序列中最初存在差异,但它们的价格表现出相对稳定。在生成交易信号时,我们将采用滚动窗口法的 Z 值法,从而无需单独的训练集和测试集。Z 值将价格序列与其历史均值标准化:
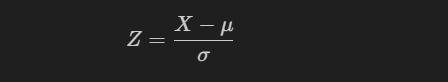
6. Where?
X 是标准化的价格;U 是滚动窗口的均值(平均值);Sigma 是滚动窗口的标准差。
Z 值衡量当前价格比偏离历史平均值的程度。Z 值高于 +1 或低于 -1 通常会触发交易信号。Z 值高于 +1 表明一种资产相对于另一种资产被高估了,这意味着卖出被高估的资产,买入被低估的资产。
反之,如果 Z 值低于-1,则表明被低估的资产已被高估,建议卖出前者,买入后者。该策略利用均值回复动态,充分利用暂时性背离和预期回归历史均值的机会。
TRAIN = int(len(uts_sanitized["AAVE-USD"]) * 0.85)
TEST = len(uts_sanitized["AAVE-USD"]) - TRAIN
AAVE_ts = uts_sanitized["AAVE-USD"]["Adj Close"][:TRAIN]
C_ts = uts_sanitized["C"]["Adj Close"][:TRAIN]
# Calculate price ratio (AAVE-USD price / C price)
ratios = C_ts/AAVE_ts
fig, ax = plt.subplots(figsize=(12, 8))
ratios_mean = np.mean(ratios)
ratios_std = np.std(ratios)
ratios_zscore = (ratios - ratios_mean) / ratios_std
ax.plot(ratios.index, ratios_zscore, label="Z-Score", color='blue')
# Plot reference lines
ax.axhline(1.0, color="green", linestyle='--', label="Upper Threshold (1.0)")
ax.axhline(-1.0, color="red", linestyle='--', label="Lower Threshold (-1.0)")
ax.axhline(0, color="black", linestyle='--', label="Mean")
ax.set_title('AAVE-USD / C: Price Ratio and Z-Score', fontsize=18)
ax.set_xlabel('Date')
ax.set_ylabel('Price Ratio / Z-Score')
ax.legend()
plt.tight_layout()
plt.show()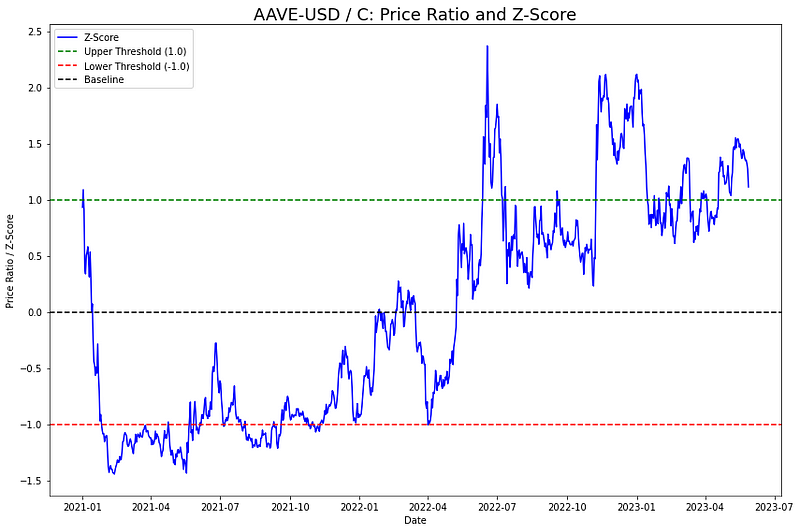
下图是一种可视化表示法,其中绿色水平线表示买入 Citigroup Inc ©,交叉时表示卖出 Aave (AAVE),而红线则表示相反。值得注意的是,该图表主要是将静止状态可视化。实际上,在应用我们的交易信号时,阈值会随着滚动窗口进行调整,以适应市场动态的变化。
现在,让我们开始执行交易信号:
def signals_zscore_evolution(ticker1_ts, ticker2_ts, window_size=15, first_ticker=True):
"""
Generate trading signals based on z-score analysis of the ratio between two time series.
Parameters:
- ticker1_ts (pandas.Series): Time series data for the first security.
- ticker2_ts (pandas.Series): Time series data for the second security.
- window_size (int): The window size for calculating z-scores and ratios' statistics.
- first_ticker (bool): Set to True to use the first ticker as the primary signal source, and False to use the second.Returns:
- signals_df (pandas.DataFrame): A DataFrame with 'signal' and 'orders' columns containing buy (1) and sell (-1) signals.
"""
ratios = ticker1_ts / ticker2_ts
ratios_mean = ratios.rolling(
window=window_size, min_periods=1, center=False).mean()
ratios_std = ratios.rolling(
window=window_size, min_periods=1, center=False).std()
z_scores = (ratios - ratios_mean) / ratios_std
buy = ratios.copy()
sell = ratios.copy()
if first_ticker:
# These are empty zones, where there should be no signal
# the rest is signalled by the ratio.
buy[z_scores > -1] = 0
sell[z_scores < 1] = 0
else:
buy[z_scores < 1] = 0
sell[z_scores > -1] = 0
signals_df = pd.DataFrame(index=ticker1_ts.index)
signals_df['signal'] = np.where(buy > 0, 1, np.where(sell < 0, -1, 0))
signals_df['orders'] = signals_df['signal'].diff()
signals_df.loc[signals_df['orders'] == 0, 'orders'] = None
return signals_df
AAVE_ts = uts_sanitized["AAVE-USD"]["Adj Close"]
C_ts = uts_sanitized["C"]["Adj Close"]
plt.figure(figsize=(26, 18))
signals_df1 = signals_zscore_evolution(AAVE_ts, C_ts)
profit_df1 = calculate_profit(signals_df1, AAVE_ts)
ax1, _ = plot_strategy(AAVE_ts, signals_df1, profit_df1)
signals_df2 = signals_zscore_evolution(AAVE_ts, C_ts, first_ticker=False)
profit_df2 = calculate_profit(signals_df2, C_ts)
ax2, _ = plot_strategy(C_ts, signals_df2, profit_df2)
ax1.legend(loc='upper left', fontsize=10)
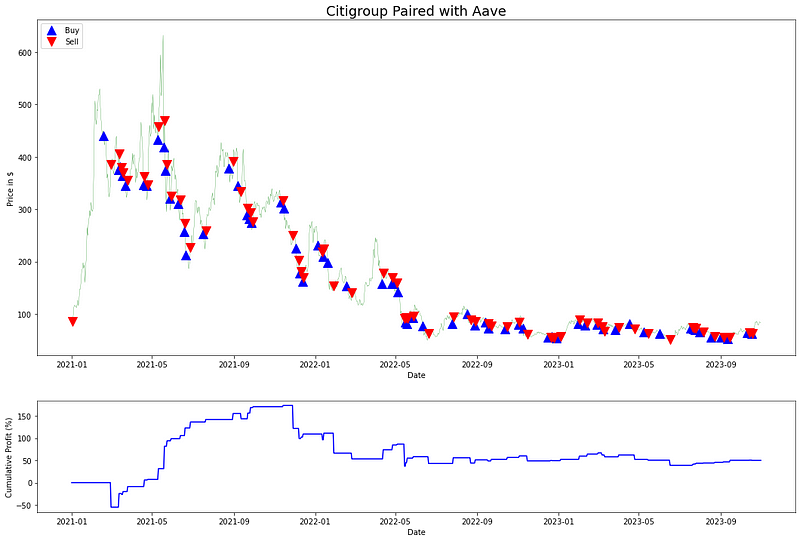
ax1.set_title(f'Citigroup Paired with Aave', fontsize=18)
ax2.legend(loc='upper left', fontsize=10)
ax2.set_title(f'Aave Paired with Citigroup', fontsize=18)
plt.tight_layout()
plt.show()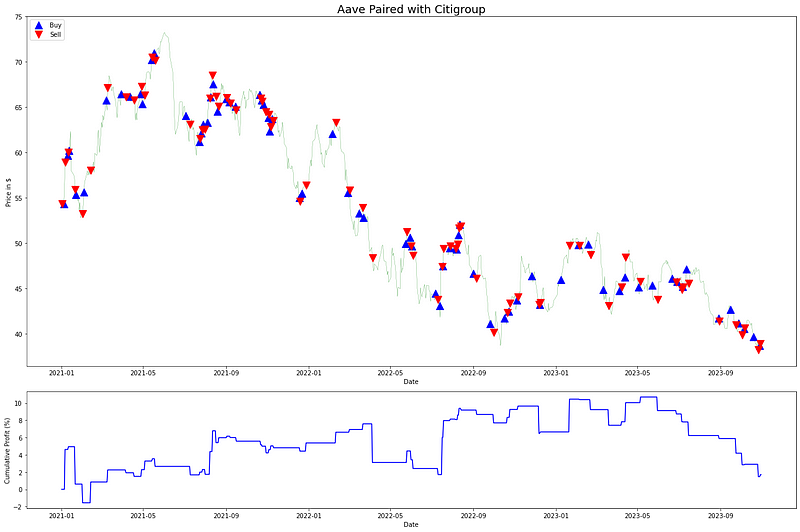
在算法交易系统中,多个交易信号往往同时运行。因此,为了捕捉整体表现,通常会汇总所有信号的收益。让我们继续计算相应的累计回报。
plt.figure(figsize=(12, 6))
cumulative_profit_combined = profit_df1 + profit_df2
ax2_combined = cumulative_profit_combined.plot(
label='Profit%', color='green')
plt.legend(loc='upper left', fontsize=10)
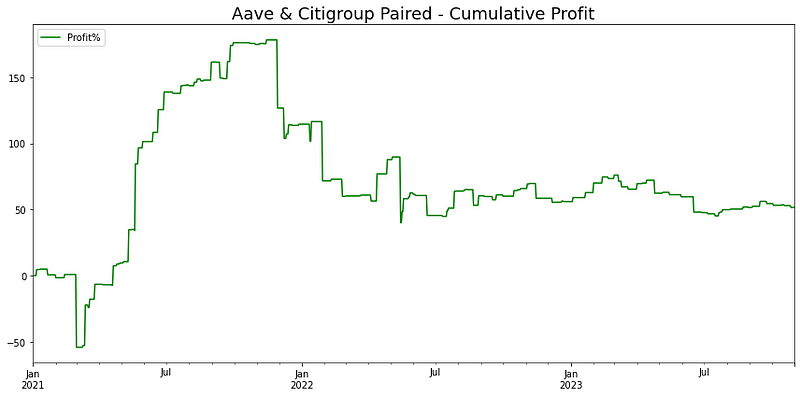
plt.title(f'Aave & Citigroup Paired - Cumulative Profit', fontsize=18)
plt.tight_layout()
plt.show()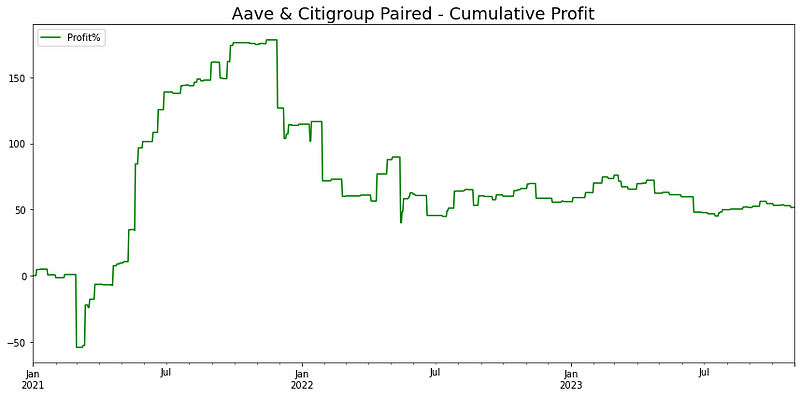
在分析的这段时间里,尽管货币对交易策略缩水了 50%,但它的表现依然强劲,账面回报率高达 100%。这一成绩超过了标准普尔 500 指数两年 10% 的回报率。不过,该策略的方差较高,这可能是由于与花旗集团配对的加密货币存在不稳定性。
6. 观点回顾
在实践中,量化分析师使用风险调整指标(如 Sortino 比率)来评估策略绩效,该指标侧重于下行风险。
总之,我们对配对交易策略的关键要点进行了探讨,涵盖了其市场中性的方式、对 Z 值和协整等统计工具的依赖,以及对均值回归的运用。不过,在实际应用这一策略时,可能会面临一些挑战,例如交易成本以及资产相关性或协整性的非平稳性风险。最后回顾本文如下:
配对交易策略:依赖于两个资产价格稳定性的策略,利用价格趋同获利。
数据处理:重要性在于确保数据的完整性和准确性,以便进行准确的分析。
市场事件影响:市场事件(如 FTX 丑闻)可能影响资产之间的关系,协整性分析有助于识别这些变化。
统计方法:使用相关性、协整性和 Z-score 等统计方法来识别交易机会和生成交易信号。
风险和实际应用:在实际交易中,需要考虑交易成本和资产相关性的非平稳性,并使用风险调整指标来评估策略表现。
可视化:通过热图和柱状图等可视化工具,有助于直观地理解资产关系和交易策略的效果。
策略评估:使用风险调整的指标(如 Sortino 比率)来评估策略的实际表现。
本文内容仅仅是技术探讨和学习,并不构成任何投资建议。
转发请注明原作者和出处。
原文地址:https://blog.csdn.net/weixin_70955880/article/details/142345663
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
