C#：判断点是否在多边形内

原理：

奇偶规则射线法：多边形内任意一点，向任意方向射线，相交数必然为奇数。

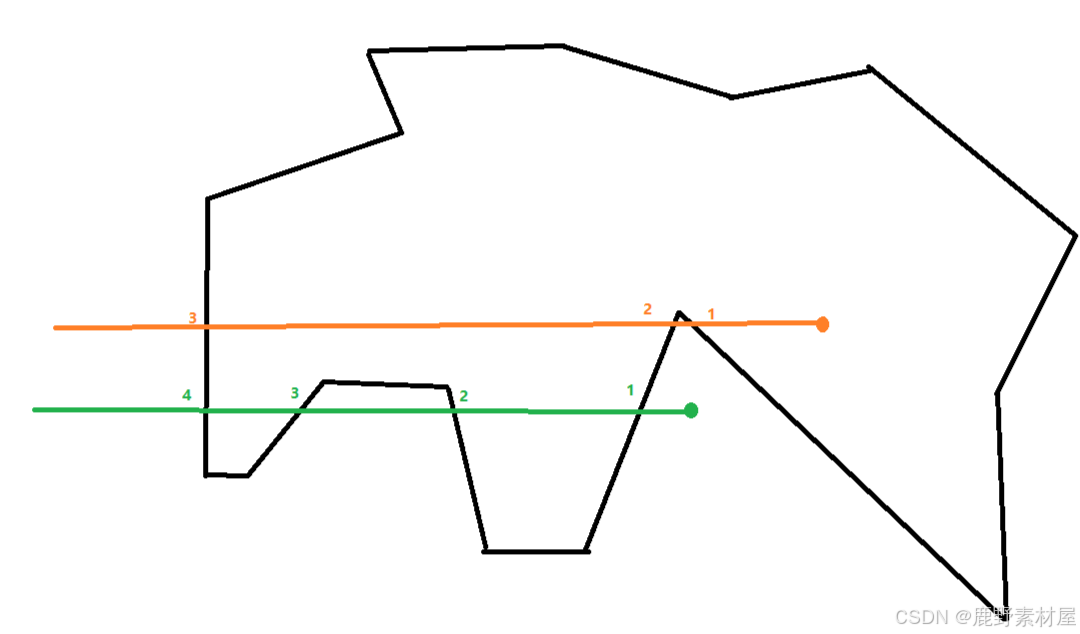
接着我们就可以利用线段到线段的相交数，求出想要的结果。

using System.Collections.Generic;
using System;
using UnityEngine;
using System.Drawing;



public class TestTools : MonoBehaviour
{

    public List<Transform> tranPos = new List<Transform>();

    // Start is called once before the first execution of Update after the MonoBehaviour is created
    void Start()
    {
      
    }


    Point GetNode(Transform _t)
    {
        var _nod = new Point(_t.position.x, _t.position.z);
        return _nod;
    }

    private void Update()
    {
        if (Input.GetKeyDown(KeyCode.A)) IsIn();
    }





    void IsIn()
    {
        var polygon = new List<Point>();
        polygon.Add(GetNode(tranPos[0]));
        polygon.Add(GetNode(tranPos[1]));
        polygon.Add(GetNode(tranPos[2]));
        polygon.Add(GetNode(tranPos[3]));


        Point point = GetNode(tranPos[4]);
        Point _pEnd = new Point(100,point.Y) ;

        int _num = 0;//相交数量
        for (var _i = 0; _i < polygon.Count; _i++)
        {
            var _p1 = polygon[_i];
            Point _p2 = polygon[0];
            if (_i < polygon.Count - 1) _p2 = polygon[_i + 1];

            Debug.Log("~~~~~~~~!!!");
            Debug.Log(_p1.X + "   " + _p1.Y + "   " + _p2.X + "   " + _p2.Y);

            var intersect = AreSegmentsIntersecting(point, _pEnd, _p1, _p2);
            Debug.Log(intersect);
            if (intersect) _num++;
        }
        Debug.LogError("相交数" + _num);
        var _get = _num % 2 != 0;
        Debug.Log(_get ? "在多边形内" : "不在多边形内");

    }

    // 定义点结构
    public struct Point
    {
        public double X, Y;

        public Point(double x, double y)
        {
            X = x;
            Y = y;
        }
    }

    // 计算两个向量的叉积 (P2 - P1) × (P3 - P1)
    private static double CrossProduct(Point p1, Point p2, Point p3)
    {
        return (p2.X - p1.X) * (p3.Y - p1.Y) - (p2.Y - p1.Y) * (p3.X - p1.X);
    }

    // 判断点p是否在a和b之间（用于共线情况下判断是否有重叠）
    private static bool IsPointOnSegment(Point p, Point a, Point b)
    {
        return Math.Min(a.X, b.X) <= p.X && p.X <= Math.Max(a.X, b.X) &&
               Math.Min(a.Y, b.Y) <= p.Y && p.Y <= Math.Max(a.Y, b.Y);
    }

    // 判断两条线段 (p1, p2) 和 (p3, p4) 是否相交
    public static bool AreSegmentsIntersecting(Point p1, Point p2, Point p3, Point p4)
    {
        double d1 = CrossProduct(p3, p4, p1);
        double d2 = CrossProduct(p3, p4, p2);
        double d3 = CrossProduct(p1, p2, p3);
        double d4 = CrossProduct(p1, p2, p4);

        // 检查叉积是否满足线段相交条件
        if (d1 * d2 < 0 && d3 * d4 < 0)
        {
            return true;
        }

        // 检查是否共线且重叠
        if (d1 == 0 && IsPointOnSegment(p1, p3, p4)) return true;
        if (d2 == 0 && IsPointOnSegment(p2, p3, p4)) return true;
        if (d3 == 0 && IsPointOnSegment(p3, p1, p2)) return true;
        if (d4 == 0 && IsPointOnSegment(p4, p1, p2)) return true;

        return false;
    }

    public static void Main()
    {
        Point p1 = new Point(0, 0);
        Point p2 = new Point(2, 2);
        Point p3 = new Point(0, 2);
        Point p4 = new Point(2, 0);

        bool intersecting = AreSegmentsIntersecting(p1, p2, p3, p4);
        Console.WriteLine("Are the segments intersecting? " + (intersecting ? "Yes" : "No"));
    }


}

简化函数为：

 public bool IsInPolygon(Point _p, List<Point> _polygon)
 {
     // 计算两个向量的叉积 (P2 - P1) × (P3 - P1)
     double CrossProduct(Point p1, Point p2, Point p3)
     {
         return (p2.X - p1.X) * (p3.Y - p1.Y) - (p2.Y - p1.Y) * (p3.X - p1.X);
     }

     // 判断点p是否在a和b之间（用于共线情况下判断是否有重叠）
    bool IsPointOnSegment(Point p, Point a, Point b)
     {
         return Math.Min(a.X, b.X) <= p.X && p.X <= Math.Max(a.X, b.X) &&
                Math.Min(a.Y, b.Y) <= p.Y && p.Y <= Math.Max(a.Y, b.Y);
     }

     // 判断两条线段 (p1, p2) 和 (p3, p4) 是否相交
     bool AreSegmentsIntersecting(Point p1, Point p2, Point p3, Point p4)
     {
         double d1 = CrossProduct(p3, p4, p1);
         double d2 = CrossProduct(p3, p4, p2);
         double d3 = CrossProduct(p1, p2, p3);
         double d4 = CrossProduct(p1, p2, p4);

         // 检查叉积是否满足线段相交条件
         if (d1 * d2 < 0 && d3 * d4 < 0)
         {
             return true;
         }

         // 检查是否共线且重叠
         if (d1 == 0 && IsPointOnSegment(p1, p3, p4)) return true;
         if (d2 == 0 && IsPointOnSegment(p2, p3, p4)) return true;
         if (d3 == 0 && IsPointOnSegment(p3, p1, p2)) return true;
         if (d4 == 0 && IsPointOnSegment(p4, p1, p2)) return true;

         return false;
     }

     Point _pEnd = new Point(float.MaxValue, _p.Y);

     int _num = 0;//相交数量
     for (var _i = 0; _i < _polygon.Count; _i++)
     {
         var _p1 = _polygon[_i];
         Point _p2 = _polygon[0];
         if (_i < _polygon.Count - 1) _p2 = _polygon[_i + 1];

         Debug.Log("~~~~~~~~!!!");
         Debug.Log(_p1.X + "   " + _p1.Y + "   " + _p2.X + "   " + _p2.Y);

         var intersect = AreSegmentsIntersecting(_p, _pEnd, _p1, _p2);
         Debug.Log(intersect);
         if (intersect) _num++;
     }
     Debug.LogError("相交数" + _num);
     var _get = _num % 2 != 0;
     Debug.Log(_get ? "在多边形内" : "不在多边形内");
     return _get;


 }


 // 定义点结构
 public struct Point
 {
     public double X, Y;

     public Point(double x, double y)
     {
         X = x;
         Y = y;
     }
 }

除了顶点照顾不到，基本也够用了。

原文地址：https://blog.csdn.net/Tel17610887670/article/details/143911811

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！