数据结构-树
目录
01、满二叉树
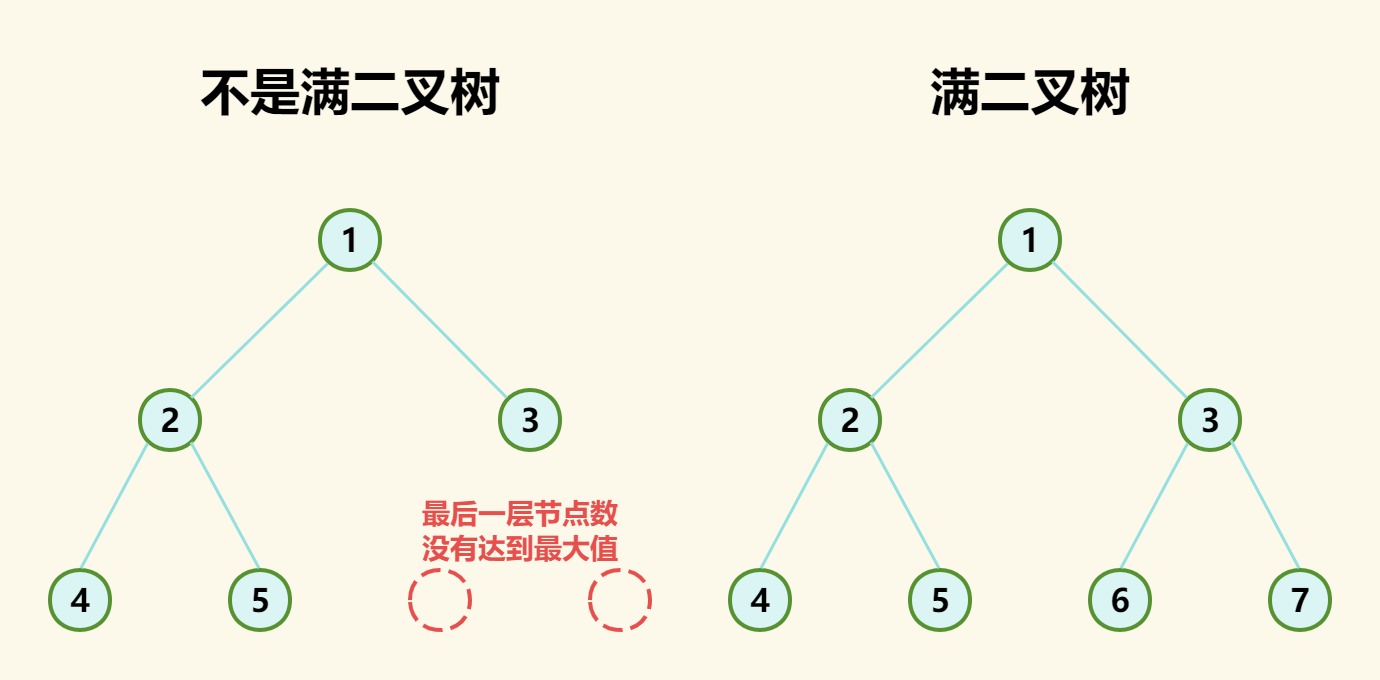
如果一个二叉树,除最后一层节点外,每一层的节点数都达到最大值,即每个节点都有两个子节点,同时所有叶子节点都在最后一层,则这个二叉树为满二叉树。
因此可以得到满二叉树有以下性质:
(1)树的最大层数为k(k>=0,即层数从0开始),则第i层的节点总数为2i,树的叶子节点总数为2k ,树的总节点数为2 ^(k+1) - 1;
(2)如果已知数的总节点数为n,则树的最大层数为k=log2(n+1) - 1(k>=0,即层数从0开始);
(3)从树的顶层开始从上到下,从左到右,对每个节点按顺序进行编号,根节点为1作为起始;
a.对于节点i,如果其存在父节点,则父节点编号为i/2向下取整;
b.对于节点i,如果其存在左节点则左节点编号为2i,如果其存在右节点则右节点编号为2i+1;
02、完全二叉树
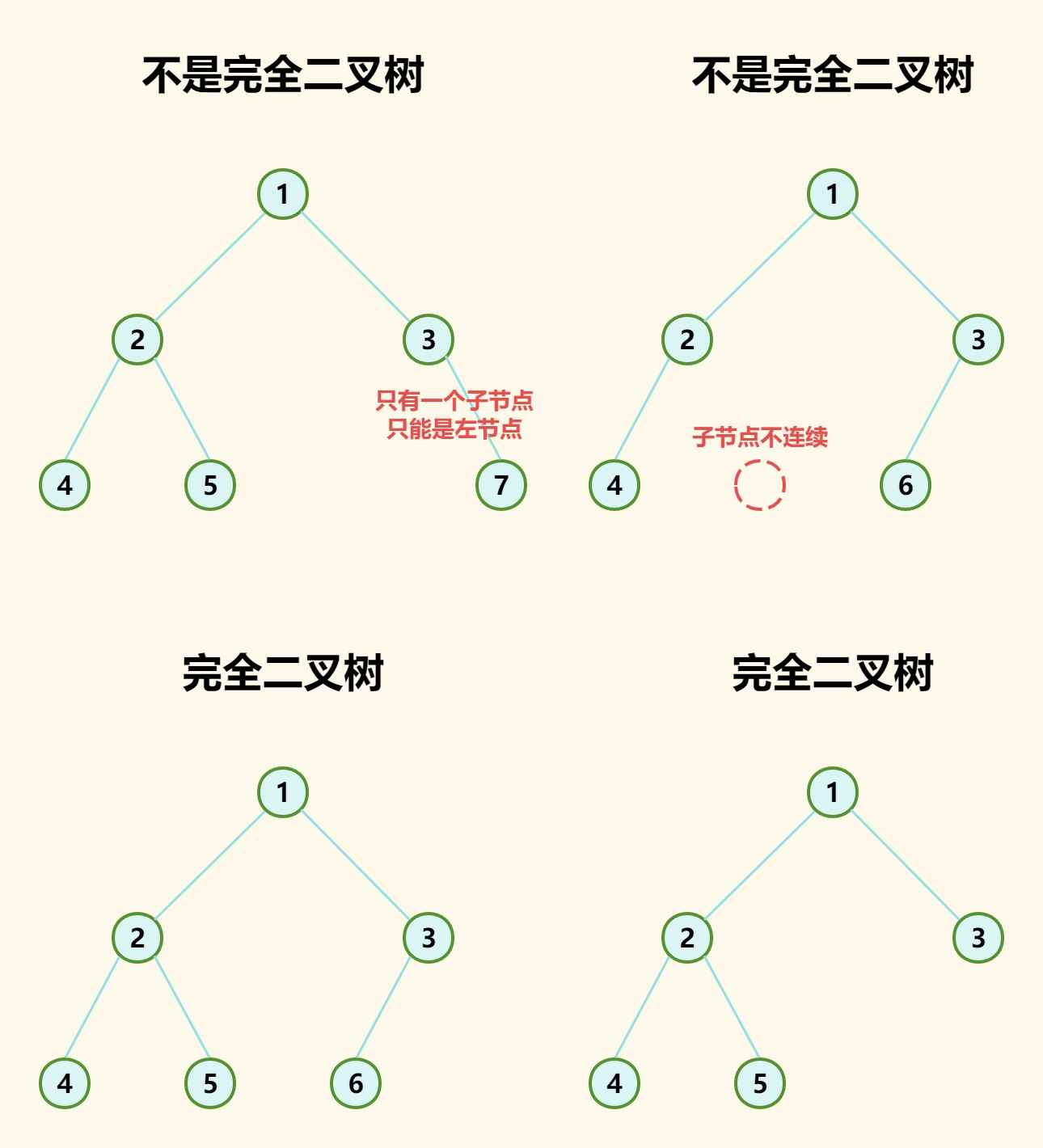
如果一棵树,叶子节点只能出现在最后两层,并且最后一层的节点都集中在左侧且从左到右是连续的。
由此我们可以得到完全二叉树有以下性质:
(1)叶子节点只能出现在倒数第一层和倒数第二层;
(2)倒数第一层的所有叶子节点都集中此层最左侧连续位置;
(3)倒数第二层如果存在叶子节点则层的所有叶子节点都集中在此层最右侧连续位置;
(4)所有节点中如果存在一个节点只有一个子节点,则此节点一定在倒数第二层,并且这个子节点一定是左节点;
(5)满二叉树一种特殊的完全二叉树;
(6)满二叉树性质(3)也适用于完全二叉树;
(7)如果完全二叉树不是满二叉树,则除最后一层外为满二叉树,适用满二叉树所有性质;
(8)如果节点总数为n,并且i<=n/2,则第i个节点为非叶子节点;
(9)如果节点总数为n,如果n为偶数则叶子节点数为n/2;如果n为奇数则叶子节点数为(n+1)/2;
(10)如果树的层数为k(k>=0),则树数的总节点数的访问为[2k,2(k+1) - 1)];
(11)如果已知数的总节点数为n,则树的最大层数为k=log2(n+1) (k>=0,即层数从0开始),并且k向下取整;
03、二叉搜索树
二叉搜索树是一种特殊的二叉树,又叫二叉查找树、二叉排序树,可以说这是一种为了查询而生的二叉树。
二叉搜索树有以下性质:
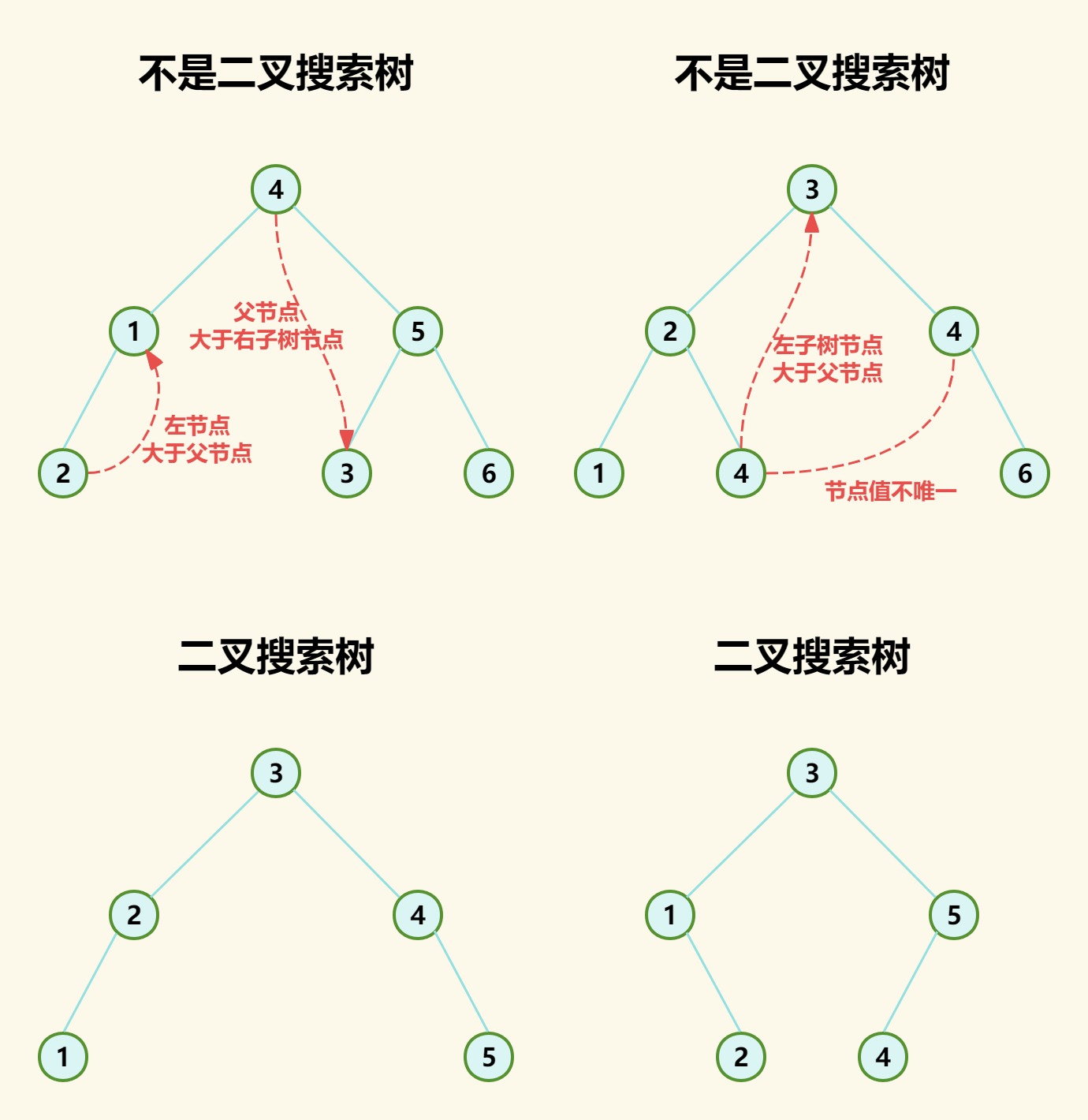
(1)每个节点值必须唯一,不能有重复值;
(2)每个节点最多有两个子节点;
(3)对于任意一个节点,如果其存在左子树则左子树上所有节点值小于该节点值,如果其存在右子树则右子树上所有节点值大于该节点值;
(3)左子树和右子树本身也各自是二叉搜索树;
04、平衡二叉树
平衡二叉树顾名思义就是使二叉树平衡在某种状态下,某种状态具体指树中任意一个节点左右子树高度差绝对值小于等于1,并且其左右子树同样也是平衡二叉树。
平衡二叉树是通过控制树的深度来优化二叉搜索树平均操作时间。
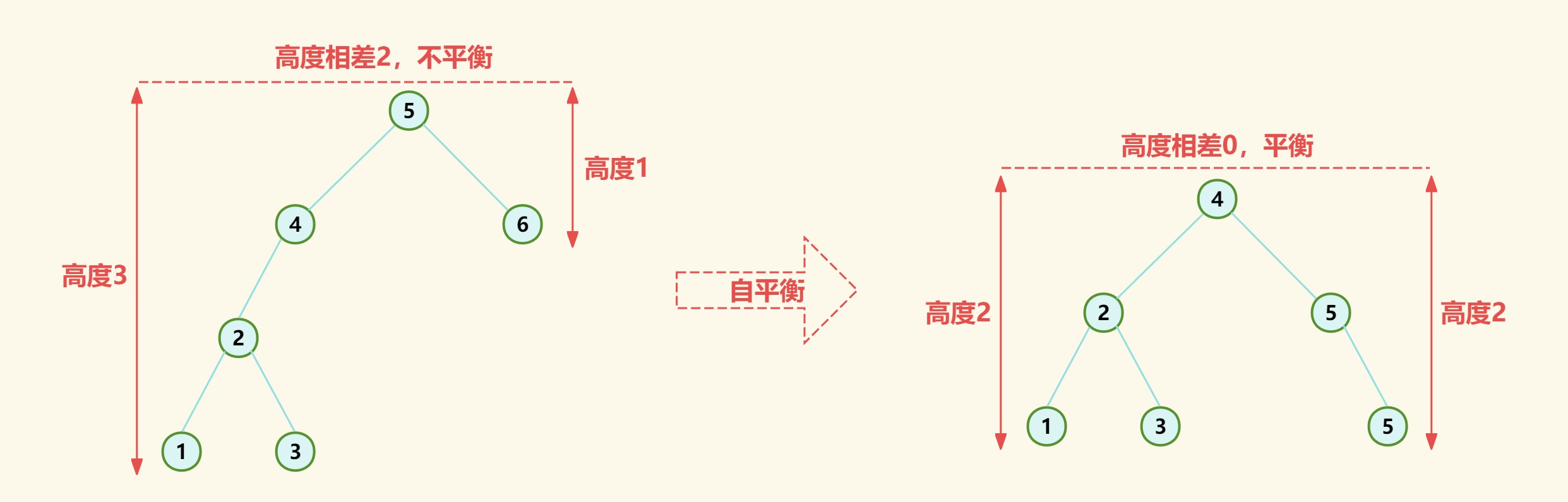
AVL树是平衡二叉树的一种特例,严格执行平衡二叉树的定义,也是最早发明的自平衡二叉搜索树。
红黑树也是一种自平衡二叉搜索树,但其并没有严格执行平衡二叉树定义,平衡条件相对比较宽松,允许左右子树高度相差绝对值大于1。
这两种树我们后面会找机会单独详细讲解。
此外还有哈夫曼树、线段树、伸展树、替罪羊树等二叉树这里就不一一介绍了,后面我们单独拿出来讲解。
05、N叉树
B树、B+树、2-3-4树、R树、Trie树等多叉树我们后面找机会单独拿出来详解。
06、存储结构
1、顺序存储
顺序存储只用一组连续的地址空间存储整个树。
当然并不是所有树都适合顺序存储的,还记得上面说的满二叉树的性质(3)吗?如果把满二叉树从上到下、从左到右,则左右子节点编号可以通过父节点编号表示。如果父节点编号为i,则其左子节点编号为2i,其右子节点编号为2i+1。而根节点作为已知起始值1,就意味着其后代节点都可以通过根节点直接或间接表示。
而编号不经让我们想到数组下标,这就意味着我们可以把整个满二叉树装进数组里。因为完全二叉树也满足满二叉树的性质(3),所以完全二叉树也可以装进数组。如下图。
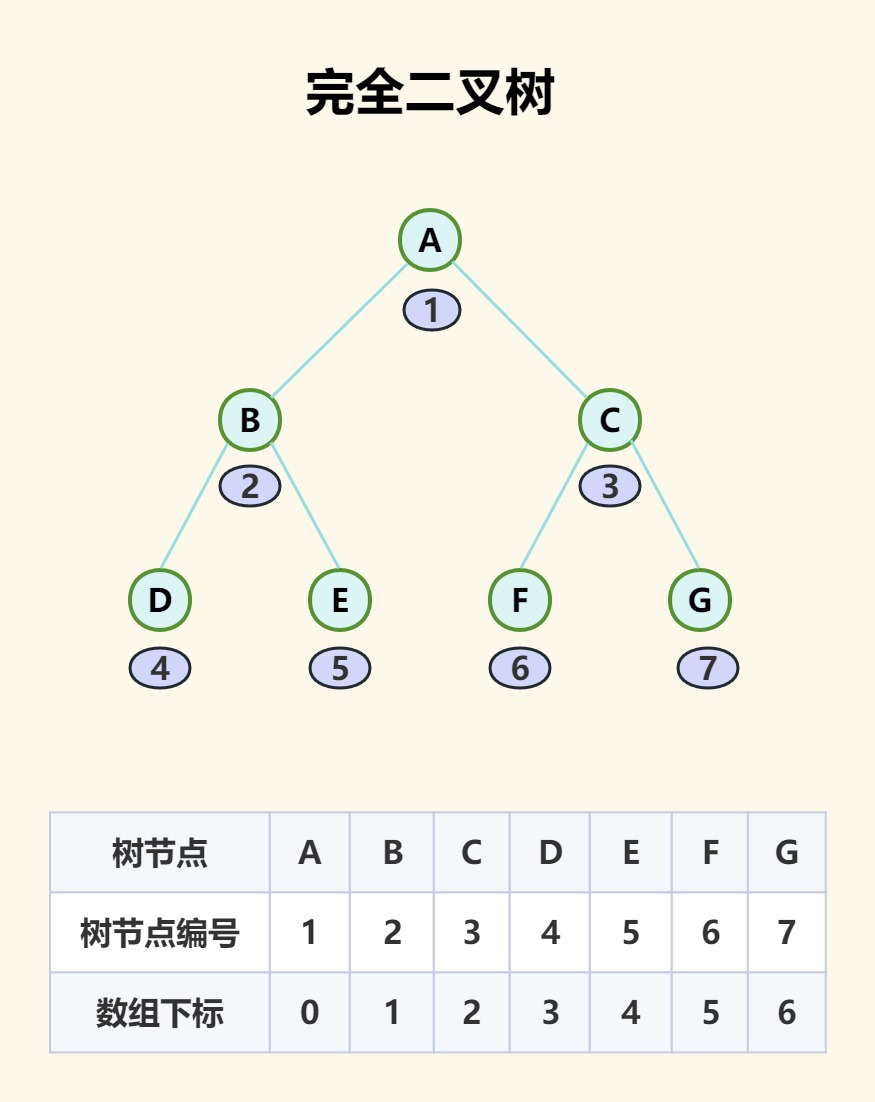
那如果非完全二叉树呢?能否放入数组中呢,答案是肯定可以的。我们只需要把非完全二叉树想象成满二叉树,把缺少的节点虚拟补全,然后对其编号,最后装入数组,入下图:
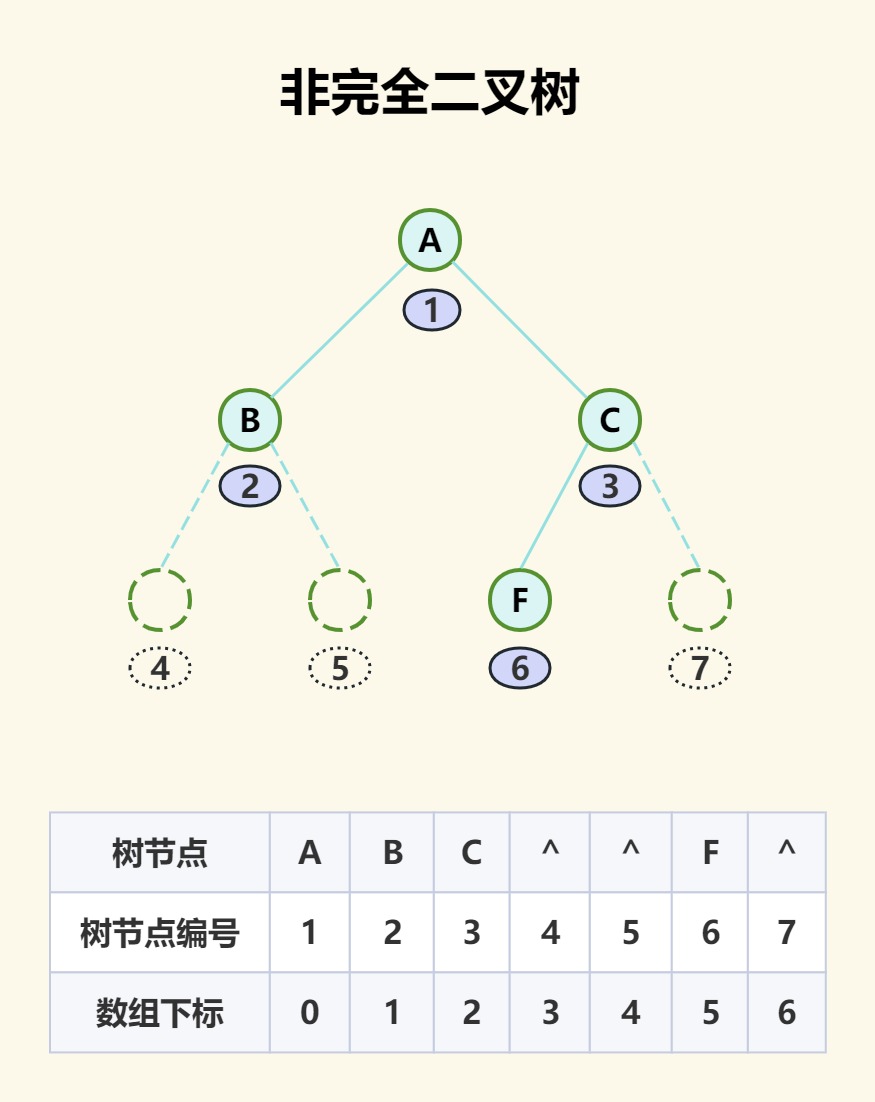
但是我们会发现编号4、5、7位都为空值,当然编号7是可以去掉的,即使如此,还是很浪费数组空间的,因此顺序存储是比较适合完全二叉树存储的,而其他类型二叉树并不是很适合。
2、链式存储
顺序存储有其局限性,因此大多数树都是使用链式存储。链式存储的核心思想就是每一个节点设计为两部分,其一为数据域存放元素值,其二为指针域存放指向子节点指针,节点有多少个子节点指针域就有多少个指针。
我们还是以二叉树为例,链式存储结构如下:
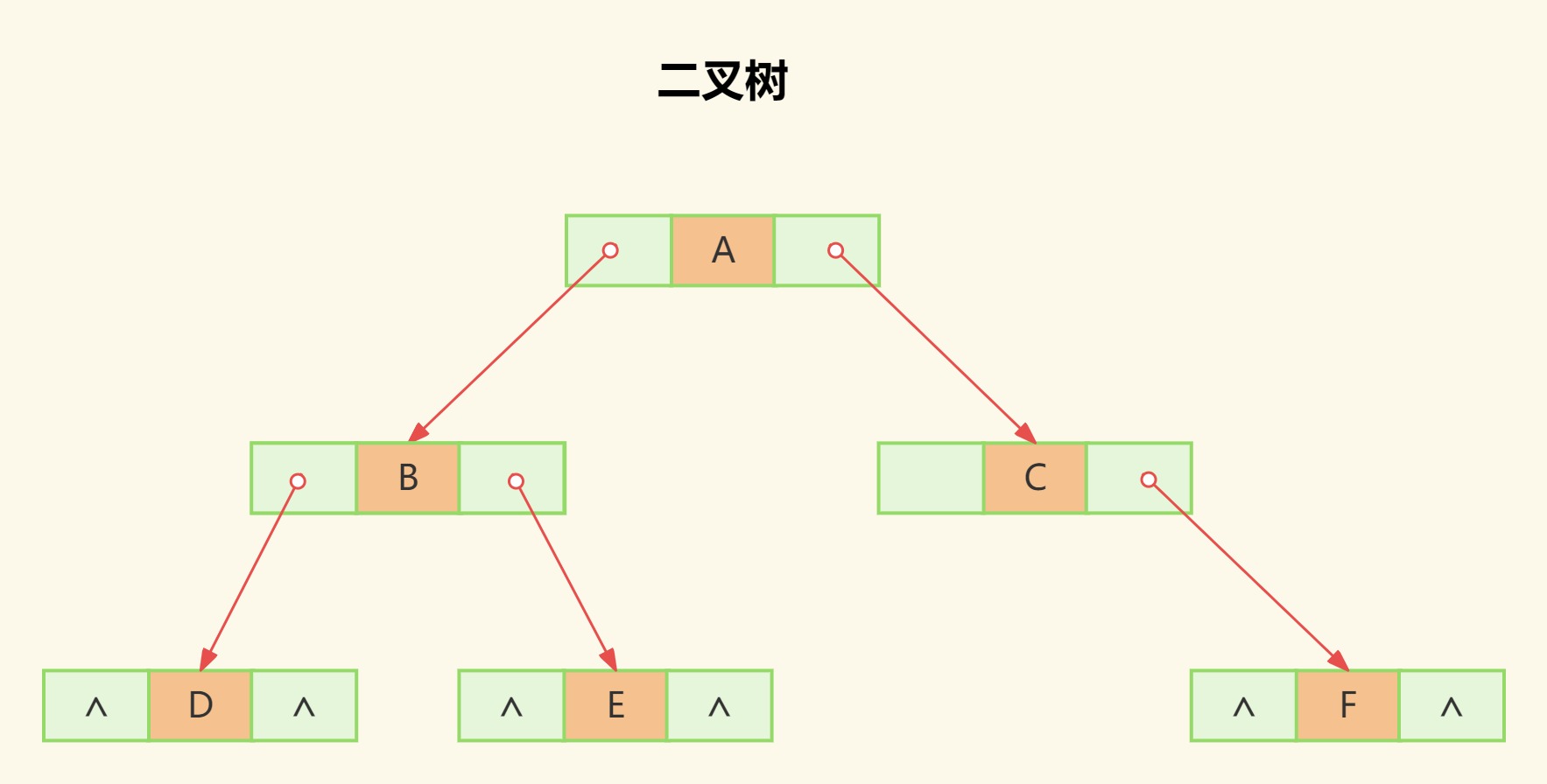
树是一种非线性数据结构,是以分支关系定义的层次结构,因此形态上和自然界中的倒挂的树很像,而数据结构中树根向上树叶向下。

什么是树?
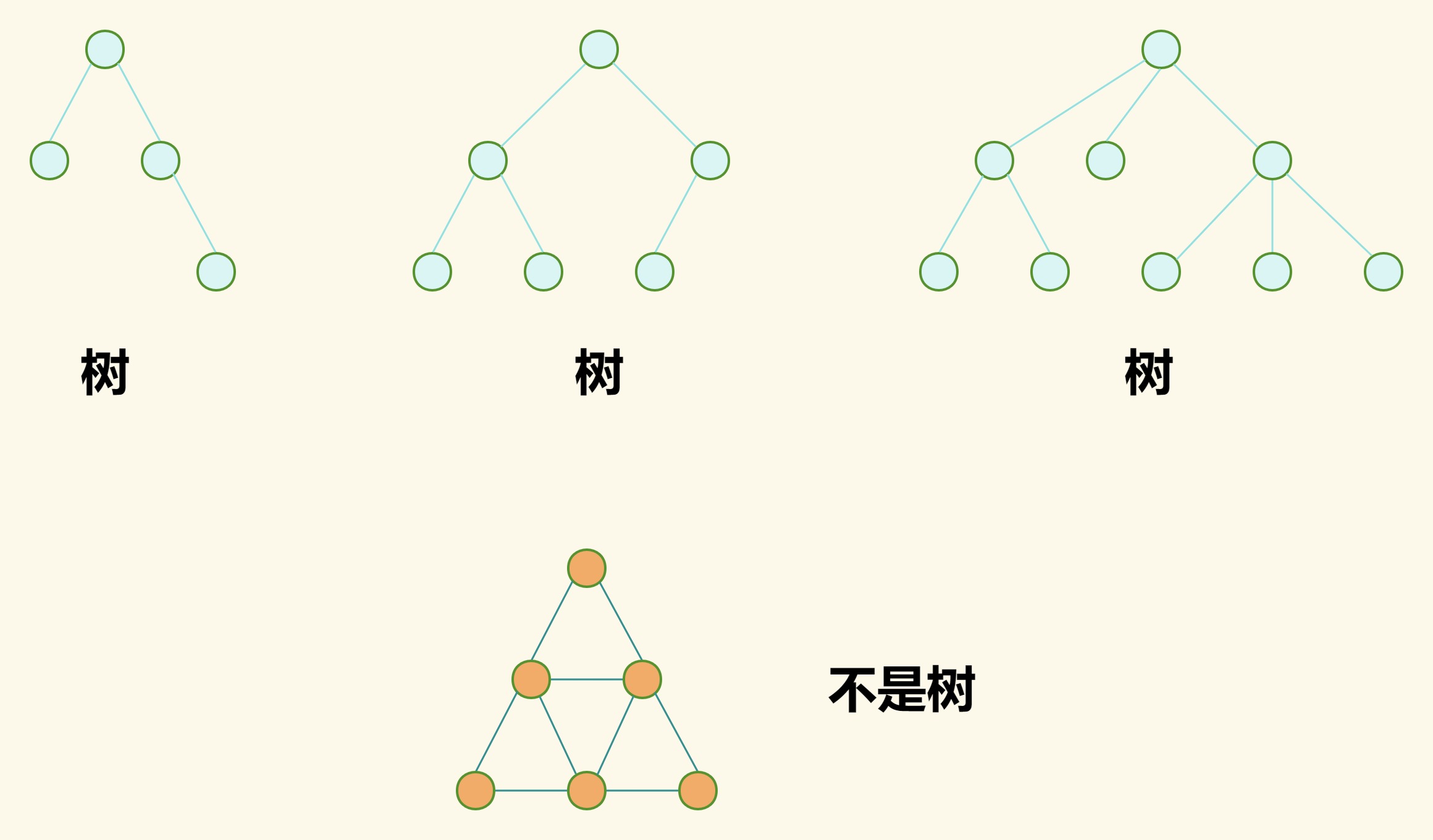
01、定义
树是由n(n>=0)个元素节点组成的有限集合,当n=0时,称为空树。
对于非空树应满足以下要求:
(1)有且仅有一个根节点;
(2)当n>1时,其余节点可分成m(m>=0)个互不相交的有限集合,其中每一个集合本身又是一棵树,称为根的子树。
从定义中我们可以得到以下结论:
1)树是分支分层结构;
2)树中仅有根节点没有父节点;
3)除根节点外,其余节点有且仅有一个父节点;
4)树中每个节点,可以有零个或多个子节点;
5)根节点到任何除自身之外的节点,有且仅有一条路径;
02、术语
1、节点相关
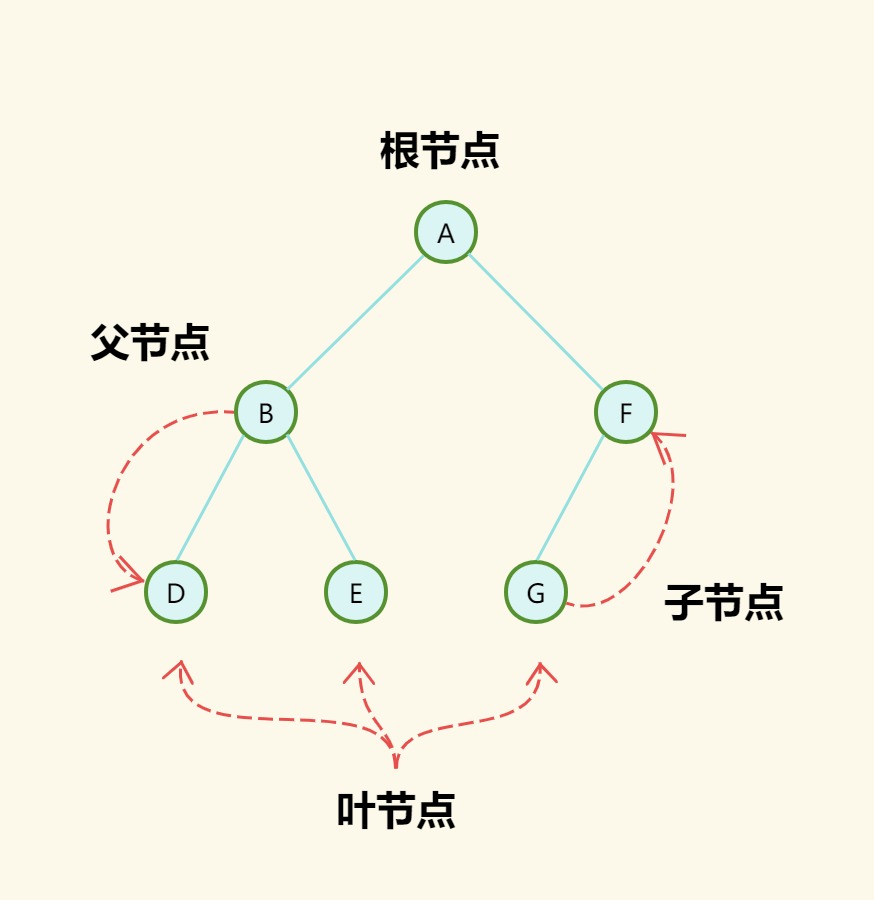
根节点:树中仅存在一个根节点,位于树的最顶层,并且其没有父节点;
叶节点:叶节点位于树的最末端,其下层没有任何节点。
子节点:某个节点的下层节点,相对于该节点叫做子节点;
父节点:某个节点的上层节点,相对于该节点叫做父节点;
2、结构相关
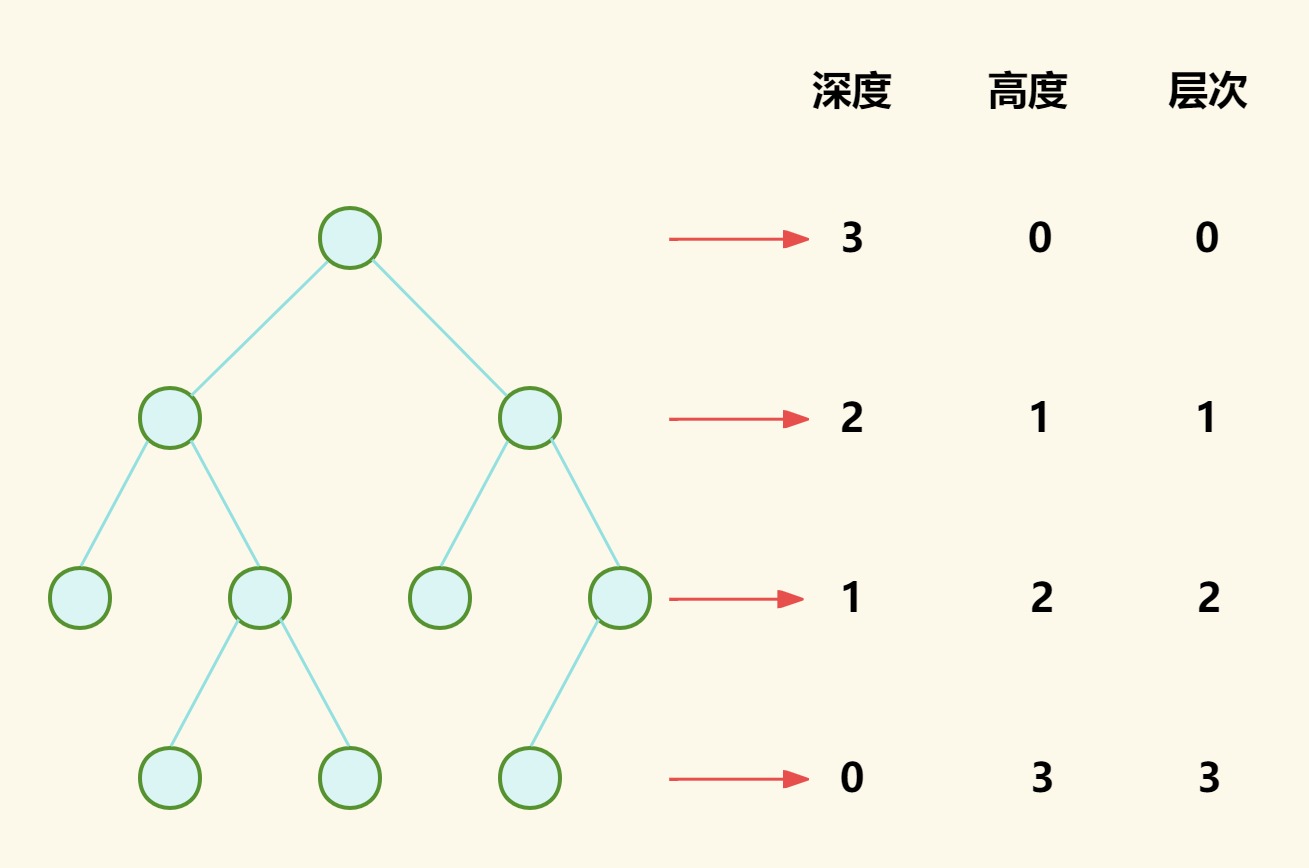
深度:从根节点到某一节点所经过的边的个数;根节点为0,其子节点为1,自上而下,以此类推。
高度:从某一节点到其最远叶节点的边数。树的高度为根节点的高度,所有叶节点高度0,其父节点为1,自下而上,以此类推。
层次:指节点所在的层级,根节点为第0层,其子节点为第1层,自上而下,以此类推。
子树:在一棵树中,任何一个以某个节点为根节点的树结构。
3、关系相关
兄弟节点:拥有共同的父节点的子节点。
祖先节点:从根节点到该节点的路径上经历的所有节点,除自身外,包括父节点、祖父节点等。
后代节点:该节点的所有下层节点,包括子节点、孙节点等。
4、其他术语
树的度:指树的宽度,也可以理解为节点的分支数,即节点的直接子节点数量,所有节点中度的最大值被视为树的度;
路径和路径长度:从一个节点到另一个节点经历的所有边的序列即为路径,路径上所有边的个数即为路径长度;
森林:指若干棵互不相交的树的集合;
03、二叉树
根据节点个数我们可以把树分成两类:二叉树和N叉树。
二叉树:每个节点最多有两个子节点的树;
n叉树:每个节点最多有n个子节点的树;
其中最常用的就是二叉树,下面我们来详细聊聊二叉树。
1、定义
(1)每个节点最多有两个子节点,分别称为左子节点和右子节点;
(2)左右子节点所构成左子树和右子树也都是二叉树;
2、性质
(1)任意一颗二叉树树,若节点数为n,则边的数量为n-1;
(2)在二叉树中,第i层最多有2^i个节点;
(3)深度为k的二叉树,总节点数最少有2k个节点,最多有2(k+1)-1个节点;
(4)在非空二叉树中,如果n0表示叶节点数量,n2表示度为2(即有两个节点)的节点数量,则n0=n2+1;
3、遍历
二叉树遍历指按照特定顺序访问二叉树中所有节点,常用的遍历方式包括:前序遍历、中序遍历、后序遍历和层次遍历。
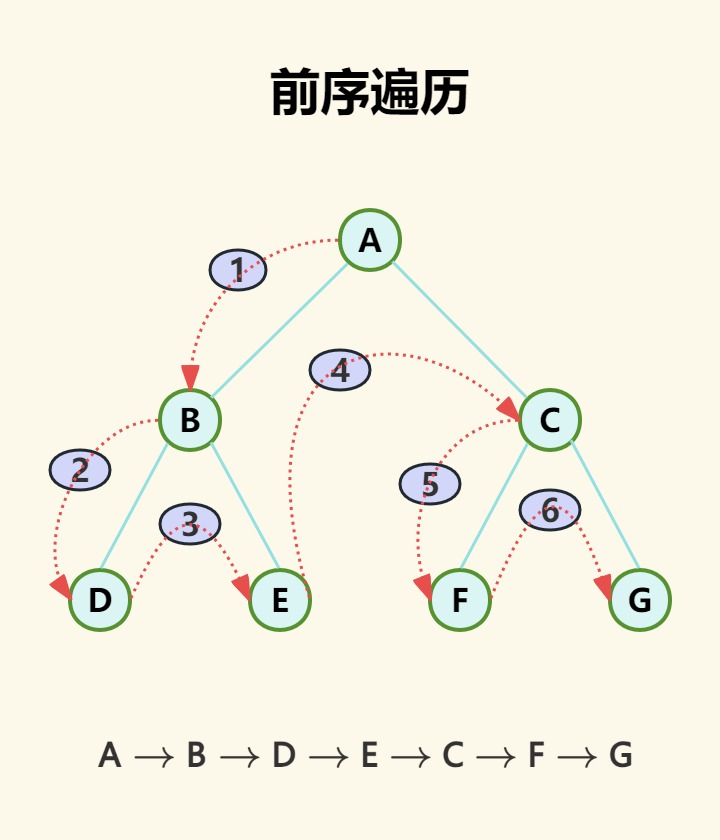
前序遍历
访问顺序:根节点->左子树->右子树
步骤:
(1)访问根结点;
(2)前序遍历左子树;
(3)前序遍历右子树。
示意图:
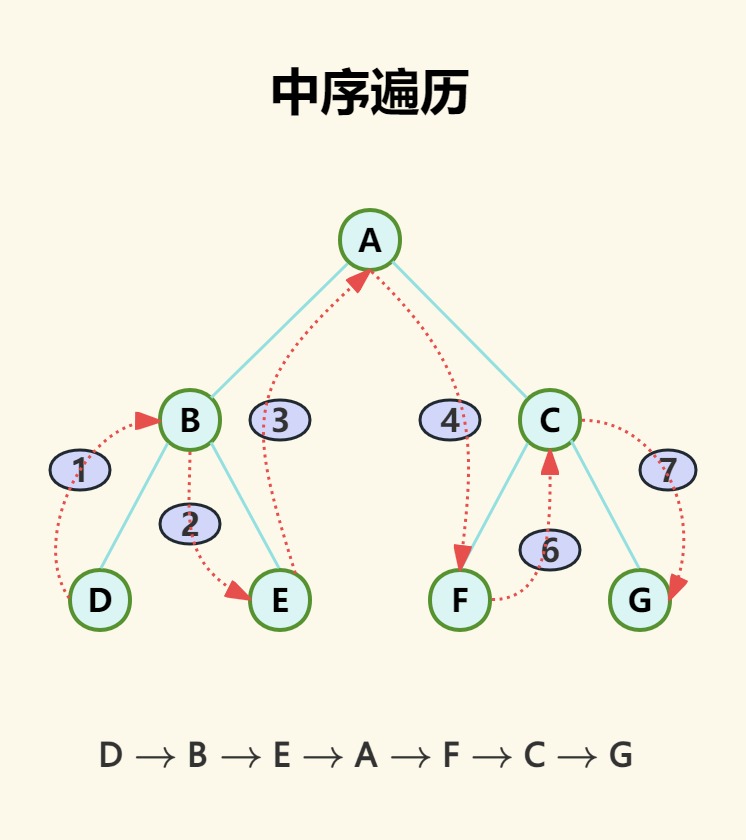
中序遍历
访问顺序:左子树->根节点->右子树
步骤:
(1)中序遍历左子树;
(2)访问根结点;
(3)中序遍历右子树。
示意图:
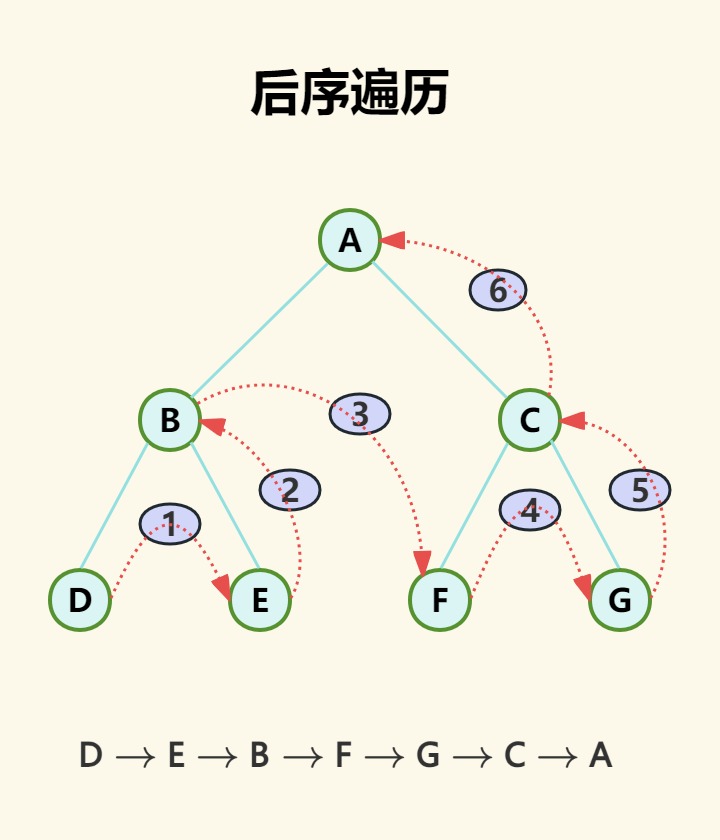
后序遍历
访问顺序:左子树->右子树->根节点
步骤:
(1)后序遍历左子树;
(2)后序遍历右子树;
(3)访问根结点;
示意图:
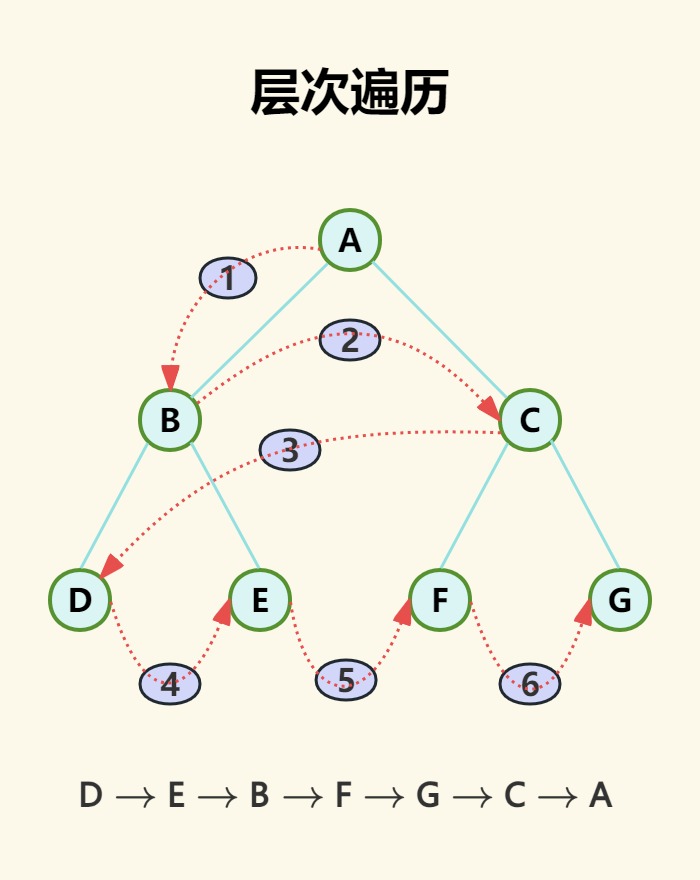
层次遍历
访问顺序:第0层->第1层->……->第n层(每层从左至右依次处理)
步骤:
(1)初始化:创建一个空队列,将根节点加入队列;
(2)遍历:
当队列不为空时:
从队列中取出一个节点,并访问该节点的值;
如果该节点有左子节点,将左子节点加入队列;
如果该节点有右子节点,将右子节点加入队列;
(3)重复步骤2,直到队列为空;
示意图:
原文地址:https://blog.csdn.net/qq_64919823/article/details/143935602
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
