AStar寻路算法

🕗 发布于 2024-11-10 05:46 算法 unity 游戏引擎

`AStar`寻路算法

（泠曦：这篇文章是个人学习所记录的笔记类文章，可能有许多不足，同时代码可能存在较多可优化内容，欢迎大家指出！）

`AStar`算法介绍

什么是`AStar`算法？

AStar算法时一个用于寻找从一个点到另一个点的启发式算法，不保证消耗最低，但可以快速找到到达终点的路径。

AStar算法在计算路劲时会不停的去获取当前离终点最近的点并刷新周围点的消耗（れいひ：但是不会刷新除边界和障碍格子以及后面提到的关闭列表中的数据），他的最终路径不一定唯一（出现不同解决方案时最终采取的解决方案取决于获取周围节点的顺序及消耗比较算法方式）。

效果图

（红色为障碍，绿色为具体路径，白色为可行走区域）

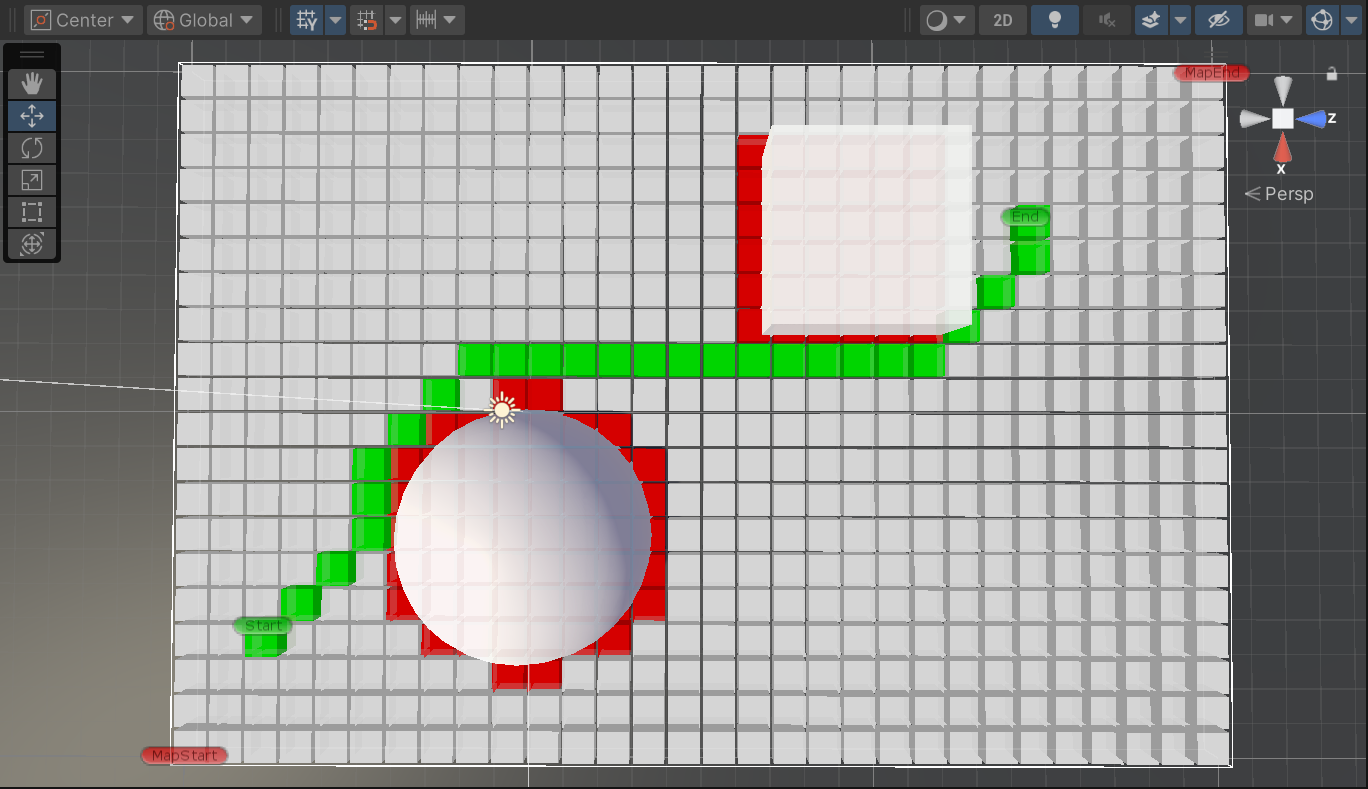
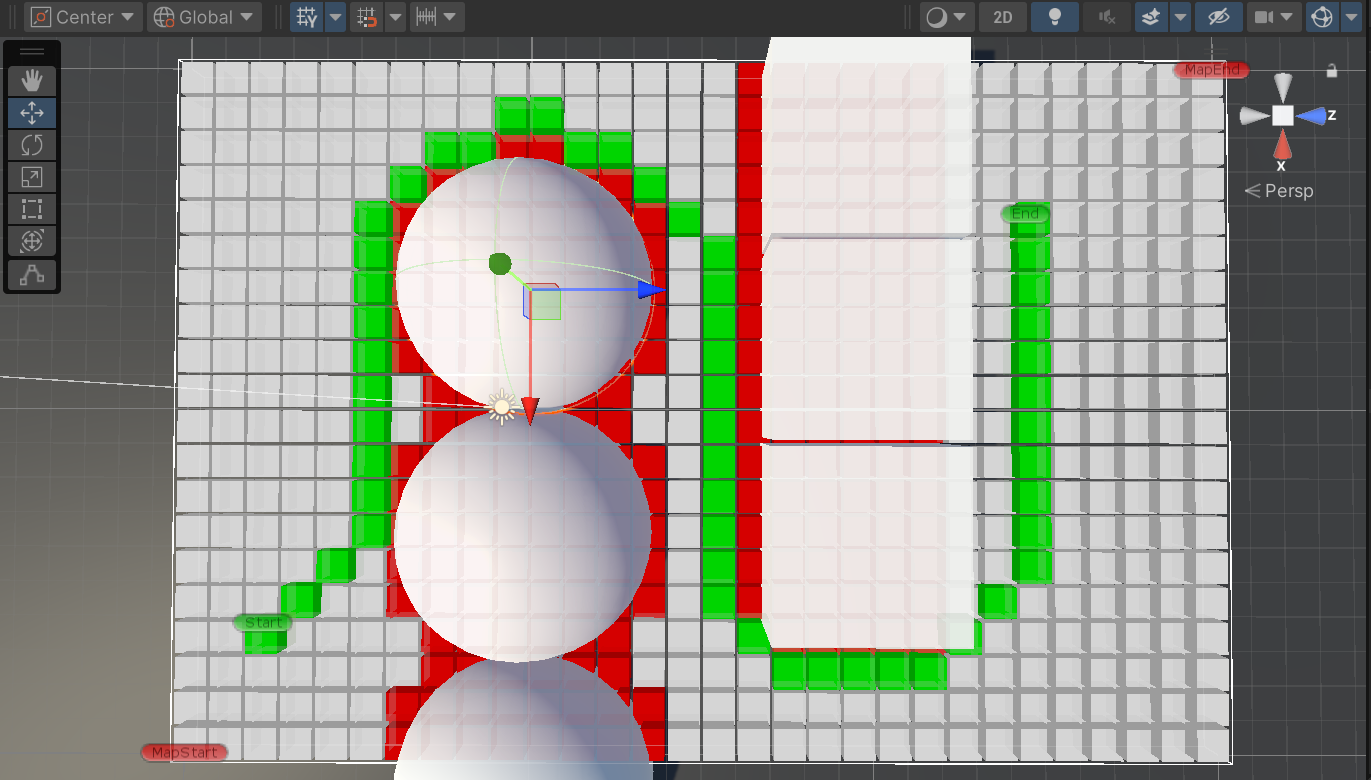
`AStar`理论基础

AStar算法实现的关键分为四个部分，寻路消耗公式、开启列表、关闭列表、当前格子的父对象。

（れいひ：这些都是什么东西呢？）
（泠曦：不要着急，下面就是是关于这些的详细介绍）

寻路消耗公式：f = g + h

在寻找路劲的时候，我们需要有一个用于确定当前路径是否为最优路径的权值（れいひ：说白了就是需要的过路费），与其他寻路算法一样，AStar计算出来的路径也是选择的所有点消耗和最小的一条，而这个公式就是用于确定每个点到终点的预估消耗及计算实际消耗。
- h：这里的h指的是当前格子离终点的预估距离，一般会采用曼哈顿距离，即计算终点横纵坐标减去当前点横纵坐标的差的绝对值之和作为该点到终点的估计距离。曼哈顿距离_百度百科
  
  （れいひ：预估距离一定要使用曼哈顿距离吗？）
  （泠曦：在实际开发中，预估距离可以自行定义计算方式的，可以根据自己的游戏项目不同行动方式不同等等进行修改，但是这里解释AStar算法时暂时统一采用曼哈顿距离进行计算。）
g：指从起点到该点的消耗，一般直接计算为从上一个点已有的消耗加上上一个点到当前点的消耗，例如从起点到a点消耗为1，从a到b点消耗为1.4，那么b点的g就为2.4.

（れいひ：这次我知道，实际开发是这些距离也可以进行对应的修改！）
（泠曦：对的，在实际开发中可能会因为地形不同等等原因导致不同点之间的消耗也不同，具体取值为什么也要符合自己的项目，不要硬性的往这里的数值上面靠哦。）
- f：预估总消耗，取值为h和g的和，用于进行排序获取当前所有点中到终点预计距离最短的点位。
开启列表

开启列表是一个用于标记格子的数组，会将所有计算了预估距离但是没有被确定路径的点存入该列表，在每一次确定路径时会取出列表中预估值最小的点作为当前节点并在计算完成后将其添加到关闭列表中。

（れいひ：为什么只将计算了预估距离的点全部放到开启列表中呢，不应该把全部点都放进去吗？）

（泠曦：因为这里的开启列表的作用是记录当前可以到达的点，并且从中选出预估总消耗最小的点，他并不是存储地图中全部点信息的列表。）
关闭列表

关闭列表和开启列表一样，也是用于标记格子的列表，不同的是他存储的是已经确定的格子，存放在关闭列表中的格子将不会被操作。

（れいひ：为什么在关闭列表中的格子是已经确定了的点呢？）
（泠曦：首先我们是从起点开始向周围遍历，每次取预估距离最短的点，那么我们每一次确定的点都将会是我们目前通过它可能到达终点的最优的解法，换句话说我们只有走这条路径经由这个点才会使最优解，尽管最终确定的路线可能不会通过这个点，但他在当前绝对会是最优的路径。）

（れいひ：也就是说，确定的点不一定是能到达重点的最终路径点，但是一定是当前预估的最佳点。）
（泠曦：是的，最后获取的可达路径也不会直接从关闭列表中进行，而是会通过下面的父对象进行反向寻找找到最佳路。）
格子的父对象

这里的父对象并不是继承关系的父对象，而是指的到达当前格子的上一个格子，用来确定每个格子到达的最短路，当遍历到终点时只需要不停的去获取终点格子的上一个格子直到起点（没有父对象），就可以获取到从起点到终点的完整路径。

（れいひ：我懂了，是不是每次找到新的点都会设置他的父对象，一直设置到终点，这样就可以在终点直接找回到起点。）
（泠曦：是的，但是这里并不只有新点才会设置父对象，而是只要没被确定下来，同时有其他点到他的距离更短就会对他的父对象进行更新，这样就可以再找到路径的同时保证消耗。）

`AStar`算法计算流程

获取起点和终点，并将起点放到CloseList中，获取起点周围的节点，更新属性并放入OpenList中。
判断OpenList是否为空：
1. 列表不为空则循环流程2345678.
2. 列表为空则证明当前可到达节点中没有节点能够达到终点，寻路结束。
获取其中f最小的节点，若多个节点f相同则获取h最小的节点（暂记为A节点）。
判断A节点是否为终点。

A节点为终点则已经找到最短路径，依次遍历父节点即获得最短路径，寻路结束。
获取A节点周围的节点。

若周围有结点在CloseList中或是边界或障碍，则直接忽略该节点。
计算A到周围节点的f值，如果比原来更小则更新该节点的参数。
判断周围节点是否在OpenList中，如果不存在则添加进去。
将A节点添加到CloseList中。

具体流程图大致如下：

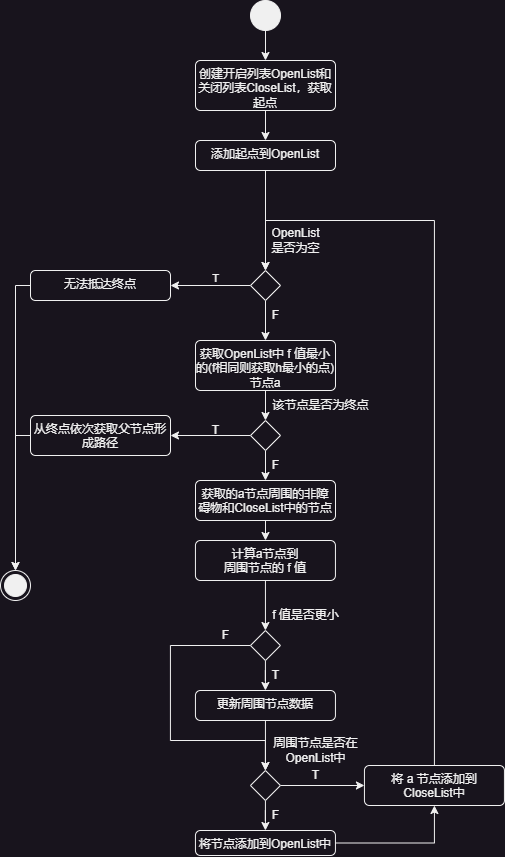
AStar寻路算法-流程图

具体计算图示

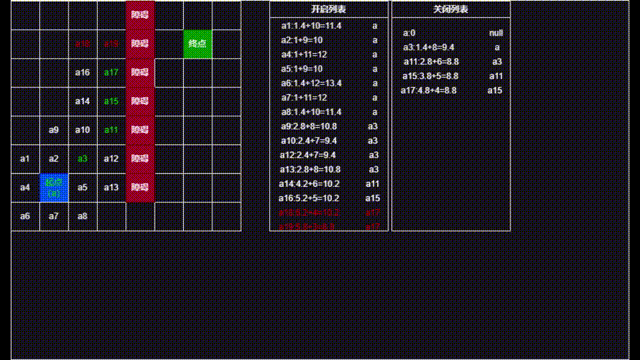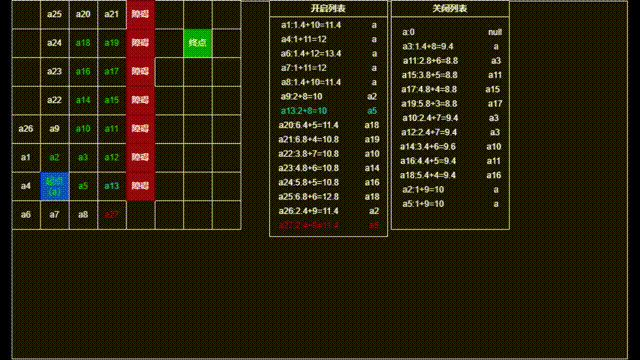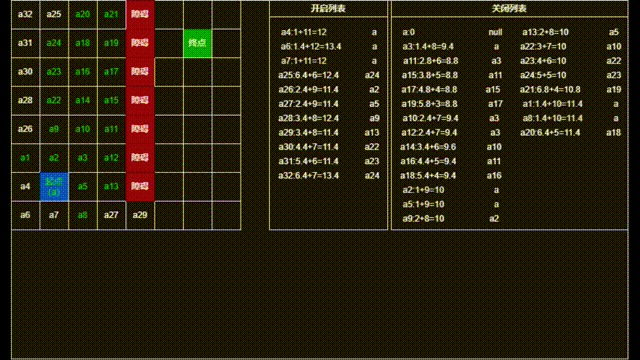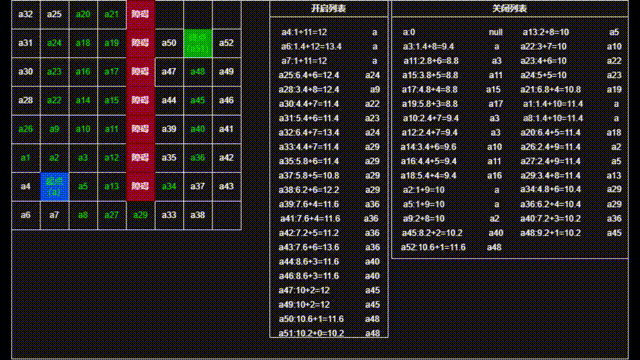
为了更直观的了解到AStar算法的计算逻辑，准备了如下图的一张地图来进行寻路，其中起点和终点如图所示，在途中还添加了障碍（红色方块），设定为横线开销为1，对角线为1.4。

（れいひ：这里的消耗设置有什么讲究吗？）
（泠曦：这里只是举例，最终设置的时候请根据实际情况来确定哦。）

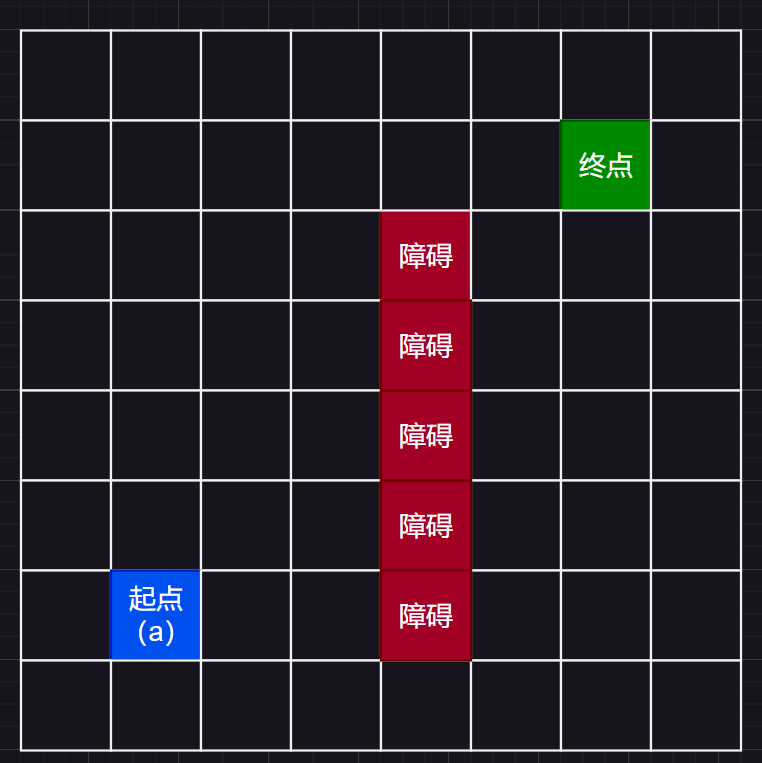
下面就是算法具体计算流程，其中绿色为已确定路径的点（CloseList中的点），红色为新搜索到的点，白色为已经添加到OpenList的点，可以看见最终搜索出了一条准确绕过障碍物的开销最小的点（列表中显示顺序为当前节点: g + h = f 父节点）。

（れいひ：这里的动画是怎么制作的？）
（泠曦：你猜，我是绝对不会说一个字一个字地点，弄了十多张图片再拼接成视频再转换为gif的。）

AStar算法无死路版——使用Clipchamp制作 00_00_00-00_00_30

除了这种最简单的情况外，还准备了一张特殊情况的图，即堵住了上面的通路将上方改成死路，我们再来看他是如何寻路的。

不同颜色代编的含义与前面相同，不同的是增加了蓝色来代表被更新的点。

（泠曦：下面的gif动图中后半部分存在计算问题，因为是手动计算，计算时在部分f值相等的点上比较时没有按照h最小的进行取值，而是直接从上往下取值，导致计算次数偏多，后续有时间会更正过来=.=）。

（れいひ：你就是懒！）
（泠曦：gun(* ￣︿￣)。）

AStar算法有死路版——使用Clipchamp制作 00_00_00-00_00_30

`Astar`算法实现

（泠曦：节点数据类定义、地图类定义等相关性不高的类仅供参考，可自行按需求调整。）

设置节点`AStarNode`

在寻路时，我们需要不停的获取到某一个节点的信息，为了便于管理可以直接将节点信息制作成一个数据类，便于我们进行操作。

在获取节点上，我们可以在地图相关类中使用一个二维数组来存储节点，那么如果每一个节点都能记录下来自己的在数组中的信息将会非常方便我们进行操作，而数组中的下标都是整数，因此只需要用整形来存储下标信息即可，所以设置成员变量gridX和gridY分别代表在数组中的下标。

（れいひ：那我可以用Vector2吗？）
（泠曦：用！都可以用！）

如果只知道在地图中的位置，就算计算出了最短路也无法应用，因为无法通过数组下标来决定下一个行走的位置，所以我们需要一个变量worldPos来存储节点的世界坐标，这里我使用Unity中的Vector3，也可以使用单独的三个变量来记录。

（れいひ：这次怎么不拆成三个变量。）
（泠曦：用！都可以用！）

而在前面的介绍中，我们知道 AStar 的核心要点就是每个节点必须要有f、g、h三个值用于区分最短路径，并且还需要有它的父节点，所以定义浮点型变量h和g，分别预估消耗和起点到该点的总消耗，定义一个同类型变量parent来记录上一个节点。

格子分为可走和不可走，在其他情况下可能还会有山地、水面消耗不同的情况，所以需要有一个格子类型type来进行区分.

（れいひ：没有那么复杂的情况是不是可以使用布尔变量，简单还节省内存。）
（泠曦：用！都可以用！）
（れいひ：你是复读机吗……）
（泠曦：被你发现啦，不过确实是可以使用的，这里只是作为举例，提供一种思路，但具体如何解决还得看大家自己。）

/// <summary>
/// 路径结点类型
/// </summary>
public enum E_Node_Type
{
    /// <summary>
    /// 可以到达
    /// </summary>
    Walkable,
    /// <summary>
    /// 不可到达
    /// </summary>
    Obstacle,
}

using UnityEngine;

/// <summary>
/// 地图结点信息(格子类)
/// </summary>
public class AStarNode
{
    /// <summary>
    /// 节点在数组中的坐标x
    /// </summary>
    public int gridX;
    /// <summary>
    /// 节点在数组中的坐标y
    /// </summary>
    public int gridY;
    /// <summary>
    /// 节点在世界坐标中的坐标
    /// </summary>
    public Vector3 worldPos;
    /// <summary>
    /// 节点到终点的预估消耗
    /// </summary>
    public float h;
    /// <summary>
    /// 起点到当前节点的消耗
    /// </summary>
    public float g;
    /// <summary>
    /// 该路径预估总消耗
    /// </summary>
    public float F { get { return g + h; } }
    /// <summary>
    /// 节点的父节点
    /// </summary>
    public AStarNode parent;
    /// <summary>
    /// 该节点的类型
    /// </summary>
    public E_Node_Type type;

    /// <summary>
    /// 初始化节点函数
    /// </summary>
    /// <param name="gridX">节点在数组中的坐标x</param>
    /// <param name="gridY">节点在数组中的坐标y</param>
    /// <param name="worldPos">节点的世界坐标</param>
    /// <param name="type">节点的类型</param>
    public AStarNode(int gridX, int gridY, Vector3 worldPos, E_Node_Type type)
    {
        this.gridX = gridX;
        this.gridY = gridY;
        this.type = type;
        this.worldPos = worldPos;
    }
}

获取地图信息

在进行寻路前，我们需要拥有地图信息，这样才可以知道我们在哪里寻路，地图有多大等等，所以定义一个类BaseGrid，用它来实现获取地图信息、获取某一结点周围节点以及通过世界坐标来获取在地图中的位置的方法。

（泠曦：这里除了获取某一节点周围节点的内容之外，并不算是核心内容哦。）
（れいひ：对的，这里只是为了了得到地图而写的一个脚本，不过也可以简单看看，毕竟他都写出来了。）

首先我们在该类中需要有一个数组来管理所有节点，所以采用一个二维数组来进行记录：

（れいひ：为什么使用二维数组，地图如果是三维的如何解决呢？）
（泠曦：斜坡也可以映射到平面，如果是多层立体地图比如有不同楼层之类的也可以进行分层，在可以进入下一地图的点进行标记即可。）

public AStarNode[,] grids;

为了更方便后续操作，设定两个变量_gridCounX和_gridCountY来记录两个方向最多有多少的格子（判断是否出界），同时设定一个变量来存储整个平面的大小（并非数组大小）；在地图上的格子应该会有各自的大小，对地图进行不同的分区会影响到这个值，所以需要一个变量来记录当前检测的范围：

（れいひ：其实部分变量可以不用声明，比如地图大小可以通过数量和格子直径做乘法得到，但是对于频繁使用的变量，提前申请空间相比于频繁申请并释放内存更加的节省运行效率。）
（泠曦：也就是通过牺牲常驻内存来节省时间，空间换时间的做法。）

protected int _gridCountX;
protected int _gridCountY;
public Vector2 gridSize;
/// <summary>
/// 节点检测半径
/// </summary>
public float halfExtent;
public float Extent => halfExtent * 2;

接下来就是对地图的初始化，我们需要对上面的这些变量进行初始赋值操作。

定义一个函数命名为Init来进行初始化，为了使运行更加灵活，通过传入地图的对角线两点的方式来计算地图的大小；后续初始化地图节点信息时需要初始化世界坐标中的信息，如果有一个参考点，后续只需要计算该节点到参考点的在数组中的距离即可通过每个格子的半径计算出具体在世界中的坐标，所以创建一个startPos变量来记录地图数组起点的世界坐标，接下来就是对他们进行初始化：

（れいひ：为什么我实际测试的时候发现计算出来的地图大小是一条直线？）
（泠曦：这里就要稍微表扬一下Unity的坐标系了，他的==横纵坐标轴不是x和y，而是x和z==哦，不要按照平常几何中的知识进行计算。）
（れいひ：是的，当时我看着泠曦在那里打Debug打了好久，哪里的逻辑都怀疑过就是没怀疑过这里=.=）
（泠曦：闭嘴，没有的事(* ￣︿￣)）

public virtual void Init(Vector3 startPos, Vector3 endPos, float halfExtent = 0.5f)
{
    gridSize = new Vector2(Mathf.Abs(endPos.x - startPos.x), Mathf.Abs(endPos.z - startPos.z));
    this.halfExtent = halfExtent;

    _gridCountX = Mathf.RoundToInt(gridSize.x / Extent);
    _gridCountY = Mathf.RoundToInt(gridSize.y / Extent);
    grids = new AStarNode[_gridCountX, _gridCountY];

    // 获取两点的最小分量作为地图左上角
    this.startPos = new Vector3(
        Mathf.Min(startPos.x, endPos.x),
        Mathf.Min(startPos.y, endPos.y),
        Mathf.Min(startPos.z, endPos.z)
    );
}

接下来就是将地图信息记录到数组中，但是这里就出现了问题：我们如何判断哪里可以前进哪里不可以前进呢？答案是可以通过层级检测来判断，如果层级是障碍等不可前进的东西则标记为不可到达，所以添加一个LayerMask类型变量来存储这些特殊物品所在的层级。

（れいひ：为什么不在前面加上这个变量呢？）
（泠曦：我忘了www）

/// <summary>
/// 节点检测层级
/// </summary>
public LayerMask layer;

接下来就需要将信息加入到二维数组中，这时前面的格子数量的作用就体现出来了，我们可以通过不同方向的数量使用嵌套循环来对每一个格子进行初始化：

for (int i = 0; i < _gridCountX; i++)
{
    for (int j = 0; j < _gridCountY; j++)
    {
        
    }
}

对于格子的属性，横纵坐标可以直接通过循环变量i和j来进行设置，然后是格子的世界坐标，我们可以直接通过前面计算的地图起点坐标和格子直径进行计算：

（れいひ：计算方式不唯一，仅供参考。）

worldPos.x += i * Extent + halfExtent;
worldPos.z += j * Extent + halfExtent;

而对于格子的类型，我们可以通过Unity提供的方法来检测范围内是否有某一层级物体，如果有属于障碍物层级的物体，就设置为不可到达类型的格子：

if (Physics.CheckSphere(worldPos, halfExtent, layer))
{
    type = E_Node_Type.Obstacle;
}

最终直接使用这些数据进行初始化即可，这里就暂时取名为CreateGrid函数，完整代码如下：

/// <summary>
/// 创建格子数组并进行设置
/// </summary>
protected virtual void CreateGrid()
{
    for (int i = 0; i < _gridCountX; i++)
    {
        for (int j = 0; j < _gridCountY; j++)
        {
            Vector3 worldPos = startPos;
            // 计算该点在世界坐标中的位置
            worldPos.x += i * Extent + halfExtent;
            worldPos.z += j * Extent + halfExtent;
            // 默认为可以行走的路径
            E_Node_Type type = E_Node_Type.Walkable;
            // 如果检测到不可以行走则设置对应的类型
            if (Physics.CheckSphere(worldPos, halfExtent, layer))
            {
                type = E_Node_Type.Obstacle;
            }
            // 将节点记录到数组中
            grids[i, j] = new AStarNode(i, j, worldPos, type);
        }
    }
}

接下来还有一个比较重要的功能，即获得一个节点周围的节点，这里其实逻辑很简单，用这个节点看作九宫格的中心，左上角是横坐标减一纵坐标加一，右上角是横纵坐标均加一，以此类推就可以得到一个循环：

for (int i = -1; i <= 1; i++)
{
    for (int j = -1; j <= 1; j++)
    {
        
    }
}

而对于内部判断条件，我们首先要知道他是不是九宫格中心，因为中心是我们已知的点而不是需要得到的节点，所以如果循环到中心点则直接跳过这一次循环：

if (i == 0 && j == 0)
{
    continue;
}

紧接着就是判断是否越界，满足条件的才会作为结果返回：

int x = node.gridX + i;
int y = node.gridY + j;

if (x >= 0 && y >= 0 && x < _gridCountX && y < _gridCountY)
{
    neighbors.Push(grids[x, y]);
}

我们将这个函数命名为GetNeighbors，完整的代码如下：

/// <summary>
/// 获取节点周围的相邻节点
/// </summary>
/// <param name="node">中心节点</param>
/// <returns>相邻节点列表</returns>
public virtual List<AStarNode> GetNeighbors(AStarNode node)
{
    Stack<AStarNode> neighbors = new();
    for (int i = -1; i <= 1; i++)
    {
        for (int j = -1; j <= 1; j++)
        {
            if (i == 0 && j == 0)
            {
                continue;
            }

            int x = node.gridX + i;
            int y = node.gridY + j;

            if (x >= 0 && y >= 0 && x < _gridCountX && y < _gridCountY)
            {
                neighbors.Push(grids[x, y]);
            }
        }
    }
    return neighbors.ToList<AStarNode>();
}

寻路管理器`AStarManager`

（れいひ：接下来就是重点了对吧！）
（泠曦：其实，理解了原理就已经够了，实际实现有很多种方式，这里只是提出一种个人用于验证的一个方法，有特别特别特别多的地方可以优化。）

对于寻路管理器，我们只希望他事先寻路相关功能，所以并不会有其他的例如获取地图信息等等的功能存在在这个脚本中，所以开始填前面没写的坑——通过世界坐标获取地图中的位置，这里这样设置是为了实现个人想要的调用方不用在地图脚本中进行设置，而是可以直接从游戏中的任意位置进行寻路。

在前面我们存储过地图起点坐标，而任意一点再数组中的位置可以通过两点坐标轴相减再除以格子直径，最终得到的值转换为整型即可，例如起点为（1，1），起点为（10，10），格子直径为5，两点差值为（9，9），除以5后得到的结果为（1.8，1.8），转换为整形后就是（1，1），也就是在二维数组中的坐标。通过这样我们可以很容易的通过世界坐标获得具体信息：

（れいひ：为什么1.8转换为整型变成了1呢？）
（泠曦：这个问题……要不你先看看基础吧。）

public virtual AStarNode GetByWorldPositionNode(Vector3 pos)
{
    int posInGridX = (int)((pos.x - startPos.x) / Extent);
    int posInGridY = (int)((pos.z - startPos.z) / Extent);
    if (posInGridX >= 0 && posInGridX < _gridCountX && posInGridY >= 0 && posInGridY < _gridCountY)
    {
        if (grids[posInGridX, posInGridY] != null || grids[posInGridX, posInGridY].type == E_Node_Type.Obstacle)
        {
            return grids[posInGridX, posInGridY];
        }
    }
    return null;
}

首先，我们肯定要定义开启列表和关闭列表，同时对于频繁使用的地图，也可以设置一个变量来进行存储：

// 基础地图格子
private BaseGrid _grid;
// 开启列表和关闭列表
private List<AStarNode> _openList = new();
private HashSet<AStarNode> _closeList = new();

接下来就是寻路函数，第一步先要通过起点终点坐标获取到格子的信息，并判断起点终点是否合法，如果不在地图范围内就直接结束寻路函数：

// 获取起点和终点节点
AStarNode starNode = _grid.GetByWorldPositionNode(startPos);
AStarNode endNode = _grid.GetByWorldPositionNode(endPos);

// 判断起点和终点节点是否非法
if (starNode == null || endNode == null)
{
    Debug.Log("起点或终点不在地图范围内，无法寻路");
    return null;
}

如果满足条件，就开始进行寻路计算。

因为这个类可能不会只使用一次，所以里面的变量可能已经被改变，所以首先要清空开启列表和关闭列表。同理，地图也可能使用了不止一次，所以对于起点，我们要清除他的所有消耗并设置父对象为空，终点同样进行处理，并且将起点添加到开启列表中。

而具体寻路肯定绝大多数时候都不止计算一次，所以使用一个循环来进行判断，循环退出的条件大家肯定猜到了，就是寻路结束找到终点，但是寻路结束除了找到终点之外，还有一个就是无法到达终点，至于如何判断是否无法到达终点，大家可以自己想一想，这里就直接写出这两个条件：

while (_openList.Count > 0)
{
    // 如果已经在终点则结束循环
    if (node.worldPos == endNode.worldPos)
        return GeneratePath(endNode);
}

首先将当前地点添加到关闭列表，并将周围的点添加到开启列表中，对于周围点是否更新以及添加的判断，可以单独写为一个函数。首先要判断这个点是否是可以走的点以及她是否在关闭列表中：

if (node.type == E_Node_Type.Obstacle || _closeList.Contains(node))
    continue;

接下来就是判断是否在开启列表中以及更新数据，如果在开启列表中则判断节点的g值，如果g值较小则证明这条路径是到达该点更近的路径。因为无论是否在开启列表中都会使用到节点的g值来进行判断或更新，所以提前使用变量来进行存储，这里顺便将计算两点之间的距离的功能作为一个函数：

// 计算当前节点的新的g值
float tempG = centerNode.g + GetDistance(centerNode, node);
// 如果新的g值小于该节点原本的g值，或者该节点不在openList中，则进行操作
if (tempG < node.g || !_openList.Contains(node))
{
    //更新节点的g值和父节点
    node.g = tempG;
    node.parent = centerNode;
    // 如果该节点不在openList中，则加入openList，并更新节点的h值
    if (!_openList.Contains(node))
    {
        node.h = Mathf.Abs(node.gridX - endNode.gridX) + Mathf.Abs(node.gridY - endNode.gridY);
        _openList.Add(node);
    }
}

protected virtual float GetDistance(AStarNode nodeA, AStarNode nodeB)
{
    // 计算两点的坐标轴差值绝对值
    int tempX = Mathf.Abs(nodeA.gridX - nodeB.gridX);
    int tempY = Mathf.Abs(nodeA.gridY - nodeB.gridY);
    // 绝对值相等则证明在对角线位置，返回1.4f
    if (tempX == tempY)
    {
        return 1.4f;
    }
    else
    {
        return 1;
    }
}

再添加到开启列表后，我们要再次进行排序，调用官方提供的Sort函数并传入适当的排序函数即可。这里的排序则是通过比较两点的f值，如果相同就比较h值，只需要获取比较小的节点，所以可以写出下面的排序函数：

// 对openList进行排序
_openList.Sort(CompareOpenList);

protected virtual int CompareOpenList(AStarNode nodeA, AStarNode nodeB)
{
    if (nodeA.F > nodeB.F)
    {
        return 1;
    }
    else if (nodeA.F == nodeB.F && nodeA.h > nodeB.h)
    {
        return 1;
    }
    else
    {
        return -1;
    }
}

在循环退出后，我们需要返回对应的路径列表，即通过终点不断获取父对象，但需要注意的是直接获取添加到列表中顺序将是正常路径的的反序，我们需要将顺序再次给他翻转一次：

protected virtual List<AStarNode> GeneratePath(AStarNode endNode)
{
    if (endNode.parent != null)
    {
        // 获取路径
        var path = new List<AStarNode> { endNode };
        while (endNode.parent != null)
        {
            path.Add(endNode.parent);
            endNode = endNode.parent;
        }
        // 对顺序进行翻转，得到正确顺序路径
        path.Reverse();
        return path;
    }
    return null;
}

具体代码源码（含需要手动配置的测试脚本）

节点类型`E_Node_Type`

/// <summary>
/// 路径结点类型
/// </summary>
public enum E_Node_Type
{
    /// <summary>
    /// 可以到达
    /// </summary>
    Walkable,
    /// <summary>
    /// 不可到达
    /// </summary>
    Obstacle,
}

节点数据类`AStarNode`

using UnityEngine;

/// <summary>
/// 地图结点信息(格子类)
/// </summary>
public class AStarNode
{
    /// <summary>
    /// 节点在数组中的坐标x
    /// </summary>
    public int gridX;
    /// <summary>
    /// 节点在数组中的坐标y
    /// </summary>
    public int gridY;
    /// <summary>
    /// 节点在世界坐标中的坐标
    /// </summary>
    public Vector3 worldPos;
    /// <summary>
    /// 节点到终点的预估消耗
    /// </summary>
    public float h;
    /// <summary>
    /// 起点到当前节点的消耗
    /// </summary>
    public float g;
    /// <summary>
    /// 该路径预估总消耗
    /// </summary>
    public float F { get { return g + h; } }
    /// <summary>
    /// 节点的父节点
    /// </summary>
    public AStarNode parent;
    /// <summary>
    /// 该节点的类型
    /// </summary>
    public E_Node_Type type;

    /// <summary>
    /// 初始化节点函数
    /// </summary>
    /// <param name="gridX">节点在数组中的坐标x</param>
    /// <param name="gridY">节点在数组中的坐标y</param>
    /// <param name="worldPos">节点的世界坐标</param>
    /// <param name="type">节点的类型</param>
    public AStarNode(int gridX, int gridY, Vector3 worldPos, E_Node_Type type)
    {
        this.gridX = gridX;
        this.gridY = gridY;
        this.type = type;
        this.worldPos = worldPos;
    }
}

地图类`BaseGrid`

using System.Collections.Generic;
using System.Linq;
using UnityEngine;

public class BaseGrid
{
    /// <summary>
    /// 存放所有节点信息的数组
    /// </summary>
    public AStarNode[,] grids;
    /// <summary>
    /// 格子地图左下角坐标
    /// </summary>
    public Vector3 startPos;
    /// <summary>
    /// 格子的大小
    /// </summary>
    public Vector2 gridSize;
    /// <summary>
    /// 节点检测半径
    /// </summary>
    public float halfExtent;
    /// <summary>
    /// 节点检测层级
    /// </summary>
    public LayerMask layer;
    public float Extent => halfExtent * 2;
    /// <summary>
    /// 节点横坐标数量
    /// </summary>
    protected int _gridCountX;
    /// <summary>
    /// 节点纵坐标数量
    /// </summary>
    protected int _gridCountY;

    /// <summary>
    /// 初始化格子
    /// </summary>
    /// <param name="startPos">地图起点（对角线）</param>
    /// <param name="endPos">地图终点（对角线）</param>
    public virtual void Init(Vector3 startPos, Vector3 endPos, LayerMask layer, float halfExtent = 0.5f)
    {
        gridSize = new Vector2(Mathf.Abs(endPos.x - startPos.x), Mathf.Abs(endPos.z - startPos.z));
        this.halfExtent = halfExtent;

        _gridCountX = Mathf.RoundToInt(gridSize.x / Extent);
        _gridCountY = Mathf.RoundToInt(gridSize.y / Extent);
        grids = new AStarNode[_gridCountX, _gridCountY];
        this.layer = layer;

        // 获取两点的最小分量作为地图左上角
        this.startPos = new Vector3(
            Mathf.Min(startPos.x, endPos.x),
            Mathf.Min(startPos.y, endPos.y),
            Mathf.Min(startPos.z, endPos.z)
        );

        CreateGrid();
    }

    /// <summary>
    /// 创建格子数组并进行设置
    /// </summary>
    protected virtual void CreateGrid()
    {
        for (int i = 0; i < _gridCountX; i++)
        {
            for (int j = 0; j < _gridCountY; j++)
            {
                Vector3 worldPos = startPos;
                // 计算该点在世界坐标中的位置
                worldPos.x += i * Extent + halfExtent;
                worldPos.z += j * Extent + halfExtent;
                // 默认为可以行走的路径
                E_Node_Type type = E_Node_Type.Walkable;
                // 如果检测到不可以行走则设置对应的类型
                if (Physics.CheckSphere(worldPos, halfExtent, layer))
                {
                    type = E_Node_Type.Obstacle;
                }
                // 将节点记录到数组中
                grids[i, j] = new AStarNode(i, j, worldPos, type);
            }
        }
    }

    /// <summary>
    /// 通过坐标获取对应格子
    /// </summary>
    /// <param name="pos">格子坐标</param>
    /// <returns>格子对象</returns>
    public virtual AStarNode GetByWorldPositionNode(Vector3 pos)
    {
        int posInGridX = (int)((pos.x - startPos.x) / Extent);
        int posInGridY = (int)((pos.z - startPos.z) / Extent);
        if (posInGridX >= 0 && posInGridX < _gridCountX && posInGridY >= 0 && posInGridY < _gridCountY)
        {
            if (grids[posInGridX, posInGridY] != null || grids[posInGridX, posInGridY].type == E_Node_Type.Obstacle)
            {
                return grids[posInGridX, posInGridY];
            }
        }
        return null;
    }

    /// <summary>
    /// 获取节点周围的相邻节点
    /// </summary>
    /// <param name="node">中心节点</param>
    /// <returns>相邻节点列表</returns>
    public virtual List<AStarNode> GetNeighbors(AStarNode node)
    {
        Stack<AStarNode> neighbors = new();
        for (int i = -1; i <= 1; i++)
        {
            for (int j = -1; j <= 1; j++)
            {
                if (i == 0 && j == 0)
                {
                    continue;
                }

                int x = node.gridX + i;
                int y = node.gridY + j;

                if (x >= 0 && y >= 0 && x < _gridCountX && y < _gridCountY)
                {
                    neighbors.Push(grids[x, y]);
                }
            }
        }
        return neighbors.ToList<AStarNode>();
    }
}

寻路算法管理类`AStarManager`

using System.Collections.Generic;
using UnityEngine;

/// <summary>
/// A*寻路管理器
/// </summary>
public class AStarManager
{
    private static AStarManager _instance;
    public static AStarManager Instance
    {
        get
        {
            _instance ??= new AStarManager();
            return _instance;
        }
    }
    // 基础地图格子
    private BaseGrid _grid;
    // 开启列表和关闭列表
    private List<AStarNode> _openList = new();
    private HashSet<AStarNode> _closeList = new();

    /// <summary>
    /// 寻路，通过起点、终点、地图信息，返回寻得的路径
    /// </summary>
    /// <param name="startPos">起点坐标</param>
    /// <param name="endPos">终点坐标</param>
    /// <param name="grid">地图信息</param>
    /// <returns>最短路径，如果没有找到可行道路返回 null</returns>
    public List<AStarNode> FindPath(Vector3 startPos, Vector3 endPos, BaseGrid grid)
    {
        // 获取格子类
        _grid = grid;

        // 获取起点和终点节点
        AStarNode starNode = _grid.GetByWorldPositionNode(startPos);
        AStarNode endNode = _grid.GetByWorldPositionNode(endPos);

        // 判断起点和终点节点是否非法
        if (starNode == null || endNode == null)
        {
            Debug.Log("起点或终点不在地图范围内，无法寻路");
            return null;
        }

        // 清理开启列表和关闭列表
        _openList.Clear();
        _closeList.Clear();

        // 重置起点属性并将起点加入关闭列表
        starNode.g = 0;
        starNode.h = 0;
        starNode.parent = null;
        _openList.Add(starNode);

        // 重置终点的父节点
        endNode.g = 0;
        endNode.h = 0;
        endNode.parent = null;

        while (_openList.Count > 0)
        {
            // 获取最小节点
            AStarNode node = _openList[0];

            // 如果已经在终点则结束循环
            if (node.worldPos == endNode.worldPos)
                return GeneratePath(endNode);

            // 将当前点移出openList并加入closedList
            _closeList.Add(node);
            _openList.Remove(node);

            // 将该点周围的点加入openList
            AddNeighborsToOpenlist(node, endNode);
            // 对openList进行排序
            _openList.Sort(CompareOpenList);
        }

        // 当开启列表为空还没有到达终点则证明无法到达，死路，返回空路径
        return null;
    }

    /// <summary>
    /// 添加周围节点到openList，并且会更新他们的g、h值
    /// </summary>
    /// <param name="centerNode">当前节点</param>
    /// <param name="endNode">终点</param>
    protected void AddNeighborsToOpenlist(AStarNode centerNode, AStarNode endNode)
    {
        // 在传入地图中获取所有周围节点信息并依次进行操作
        foreach (var node in _grid.GetNeighbors(centerNode))
        {
            // 判断是否为障碍或该节点是否在closeList中，如果满足条件则不进行操作
            if (node.type == E_Node_Type.Obstacle || _closeList.Contains(node))
                continue;

            // 计算当前节点的新的g值
            float tempG = centerNode.g + GetDistance(centerNode, node);
            // 如果新的g值小于该节点原本的g值，或者该节点不在openList中，则进行操作
            if (tempG < node.g || !_openList.Contains(node))
            {
                //更新节点的g值和父节点
                node.g = tempG;
                node.parent = centerNode;
                // 如果该节点不在openList中，则加入openList，并更新节点的h值
                if (!_openList.Contains(node))
                {
                    node.h = Mathf.Abs(node.gridX - endNode.gridX) + Mathf.Abs(node.gridY - endNode.gridY);
                    _openList.Add(node);
                }
            }
        }
    }

    /// <summary>
    /// 获取相邻节点的实际距离（可以自行重写修改计算方式）
    /// </summary>
    /// <param name="nodeA"></param>
    /// <param name="nodeB"></param>
    /// <returns></returns>
    protected virtual float GetDistance(AStarNode nodeA, AStarNode nodeB)
    {
        // 计算两点的坐标轴差值绝对值
        int tempX = Mathf.Abs(nodeA.gridX - nodeB.gridX);
        int tempY = Mathf.Abs(nodeA.gridY - nodeB.gridY);
        // 绝对值相等则证明在对角线位置，返回1.4f
        if (tempX == tempY)
        {
            return 1.4f;
        }
        else
        {
            return 1;
        }
    }

    /// <summary>
    /// 比较两个节点相对终点的位置
    /// </summary>
    /// <param name="nodeA"></param>
    /// <param name="nodeB"></param>
    /// <returns></returns>
    protected virtual int CompareOpenList(AStarNode nodeA, AStarNode nodeB)
    {
        if (nodeA.F > nodeB.F)
        {
            return 1;
        }
        else if (nodeA.F == nodeB.F && nodeA.h > nodeB.h)
        {
            return 1;
        }
        else
        {
            return -1;
        }
    }

    /// <summary>
    /// 根据寻路终点，从终点往回找路径
    /// </summary>
    /// <param name="endNode">终点</param>
    /// <returns>路径列表</returns>
    protected virtual List<AStarNode> GeneratePath(AStarNode endNode)
    {
        if (endNode.parent != null)
        {
            // 获取路径
            var path = new List<AStarNode> { endNode };
            while (endNode.parent != null)
            {
                path.Add(endNode.parent);
                endNode = endNode.parent;
            }
            // 对顺序进行翻转，得到正确顺序路径
            path.Reverse();
            return path;
        }
        return null;
    }
}

测试脚本`TestAStar`

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class TestAStar : MonoBehaviour
{
    private BaseGrid _baseGrid = new();

    public Transform mapStart;
    public Transform mapEnd;
    public Transform start;
    public Transform end;
    public LayerMask layers;
    public List<AStarNode> path;

    public void OnStart()
    {
        _baseGrid.Init(mapStart.position, mapEnd.position, layers, 0.5f);
        StartCoroutine(GetPath());
    }

    private IEnumerator GetPath()
    {
        List<AStarNode> path = AStarManager.Instance.FindPath(start.position, end.position, _baseGrid);
        yield return null;
        this.path = path;
        yield return null;
        foreach (var node in path)
        {
            Debug.Log(node.worldPos);
            yield return new WaitForSeconds(1);
        }
    }

    private void OnDrawGizmos()
    {
        Gizmos.DrawWireCube(_baseGrid.startPos + new Vector3(_baseGrid.gridSize.x, 0, _baseGrid.gridSize.y) / 2, new Vector3(_baseGrid.gridSize.x, 1, _baseGrid.gridSize.y));
        if (_baseGrid.grids == null)
        {
            return;
        }
        foreach (var node in _baseGrid.grids)
        {
            Gizmos.color = node.type == E_Node_Type.Obstacle ? Color.red : Color.white;
            Gizmos.DrawCube(node.worldPos, Vector3.one * (_baseGrid.Extent - 0.1f));
        }


        Gizmos.color = Color.yellow;
        Gizmos.DrawCube(_baseGrid.GetByWorldPositionNode(start.position).worldPos, Vector3.one * (_baseGrid.Extent - 0.1f));
        Gizmos.DrawCube(_baseGrid.GetByWorldPositionNode(end.position).worldPos, Vector3.one * (_baseGrid.Extent - 0.1f));

        if (path != null)
        {
            Gizmos.color = Color.green;
            foreach (var node in path)
            {
                Gizmos.DrawCube(node.worldPos, Vector3.one * (_baseGrid.Extent - 0.1f));
            }
        }
    }
}

源项目文件

https://github.com/LingxiReihi/AStar.git

原文地址：https://blog.csdn.net/qq_62597193/article/details/143654357

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！

上一篇：Sequelize+Sqlite3使用示例
下一篇：【Web前端】使用 JSON 处理数据

基于spring boot的医院挂号就诊系统论文
第二点：设计有效的导航，这个包括每个页面上都有导航条的显示，有时也可以在页面的底部设计导航条，当用户进入具体页面时，要设计相应的位置提示，在页面中比较特殊的位置，需要设计返回链接，可以返回上个页面，也
阅读更多2024-11-28
【Unity踩坑】Unity中父对象是非均匀缩放时出现倾斜或剪切现象
本文解决了Unity中父对象是非均匀缩放时出现倾斜或剪切的问题
阅读更多2024-11-28
「Mac玩转仓颉内测版29」基础篇9 - 数组类型详解
本篇将介绍 Cangjie 中的数组类型，包括数组的定义、创建、访问、常见操作以及在数据管理中的应用，帮助开发者熟练掌握数组的使用。
阅读更多2024-11-28
创建mapreduce项目使用maven
创建mapreduce项目使用maven
阅读更多2024-11-28
Python开源项目周排行 2024年第16周
注:当前文章会不定期进行更新。标签： ERP PDF OCR。
阅读更多2024-11-28
使用EFK收集k8s日志
首先我们使用EFK收集Kubernetes集群中的日志，本次实验讲解的是在Kubernetes集群中启动一个Elasticsearch集群，如果企业内已经有了Elasticsearch集群，可以直接将
阅读更多2024-11-28
C#基础41-45
求n以内（不包括n）同时能被3和7整数的所有自然数之和的平方根s，并作为函数值返回，最后结果s输出到控制台。44.数组x中有n个数，求出奇数的个数cn1和偶数的个数cn2以及数组x下标为奇数的元素值的
阅读更多2024-11-28
JavaScript：遍历一个对象数组，获取每个对象中 mainKeyId 对应的值，并以这个值作为新属性的键名，给该对象添加一个新属性。
假设我们有一个对象数组，每个对象包含一个mainKeyId字段，以mainKeyId的值作为新的键名，并给它添加一个新的属性。
阅读更多2024-11-28
【AI系统】谷歌 TPU v4 与光路交换
TPU v4 通过采用 7nm 工艺，翻倍的 MXU 数量，以及显著增加的内存容量和带宽，实现了性能的大幅提升。特别引人注目的是 Sparse Core 的引入，它专门针对稀疏计算进行了优化，使得 T
阅读更多2024-11-28
SpringBoot文件上传之秒传、断点续传、分片上传
比如，在线教育平台上的视频资源上传，社交平台上的图片分享，以及企业内部的知识文档管理等。这些场景对文件上传的要求也各不相同，有的追求速度，有的注重稳定性，还有的需要考虑文件大小和安全性。这对于大文件上
阅读更多2024-11-28

AStar寻路算法