英雄联盟游戏使用生存分析预测玩家流失

1 引言

在过去的十年中，电子竞技（esports）已经成为一种受玩家和观众欢迎的形式，促进了一个庞大的行业和一个不断发展的研究领域 [19, 21, 25, 28, 37, 38]。虽然很难估计电子竞技市场的规模，但Superdata Research预测该市场在2017年将价值11亿美元，并且到2019年将有3.3亿观众，使电子竞技成为游戏学术界和产业的重要研究和发展领域。

虽然没有官方定义，Schubert等人 [25] 提出，电子竞技是指在有观众的竞争环境中进行的任何数字游戏。在电子竞技中，多人在线战斗竞技场（“MOBA”）游戏是一种越来越常见的形式，而《英雄联盟》（“LoL”）是最受欢迎的例子。LoL拥有大约1亿的月度国际玩家群体 [15]。像其他MOBA游戏一样，LoL涉及两支由五名玩家组成的队伍，各自竞争摧毁对方队伍的“基地”（Nexus），这是位于队伍基地的一个物理结构。每个玩家被称为“召唤师”，控制一个“英雄”，这是战斗中的玩家化身。截至撰写本文时，玩家可以选择超过120个英雄。除了对抗五名对手队员外，玩家还必须对抗电脑控制的怪物。击败敌人可以让玩家获得经验和金币，前者允许在当前比赛中解锁更强大的能力，而后者可以用来购买增加力量和表现的物品。

LoL是免费游戏，收入主要来自微交易，其价格范围从2美元到数百美元，允许玩家购买如英雄和英雄皮肤等物品。鉴于这些物品的边际成本几乎为零，即使只有相对少量的玩家进行这些可选购买，LoL也能够非常成功和盈利。2016年，LoL的收入达到17亿美元，是收入最高的免费在线游戏 [30]，尽管其每位玩家的平均消费仅为18.88美元，相对于其他MOBA游戏 [29]。

鉴于此，MOBA商业模式依赖于玩家留存，以便继续有玩家进行这些购买。即使只有一小部分玩家群体参与微交易，玩家越多，游戏时间越长，Riot Games（LoL的发行商）的收入就越高。此外，有证据表明，在免费增值游戏中，玩家参与的时间长短似乎与购买发生的机会相关 [17, 39]。这进一步增加了对促进长期玩家留存体验的兴趣。

公司的收入依赖于游戏内购买，这意味着了解游戏结束的预测因素对于LoL和类似游戏的持续财务成功至关重要。能够识别接近离开游戏的玩家特征行为，可以帮助公司知道何时战略性地增加服务或更具体地迎合这些玩家，以防止他们离开 [9, 23]。

因此，本文的贡献在于对LoL中玩家脱离（或“流失”）的关键预测因素进行初步调查。通过将LoL比赛视为一个重要事件，使用生存分析来预测在给定一组独立变量的情况下，从一个比赛（epoch）到另一个比赛（事件）之间将经过多少时间。生存分析通常用于分析各种行业的客户流失，但在游戏分析中的应用较少。具体来说，本文的工作扩展了先前在移动游戏的游戏时间测量和生存分析方面的工作 [34, 36]，并将其应用于更复杂的MOBA领域。

为此，应用了三种生存分析技术并比较了它们产生的结果：Kaplan-Meier估计、标准Cox回归模型和混合效应Cox回归模型。这些技术与包括最近平均比赛时间、最近平均比赛间隔时间和最高赛季段位在内的时间性玩家行为特征一起使用。这些特征主要与特定游戏无关，使得本文提出的流失分析方法可以轻松转移到更广泛的MOBA类型。

本文其余部分如下：第2节提供了跨多个行业的客户流失的更多详细信息，以及使用生存分析来识别流失的关键指标。第3节描述了本文使用的生存分析模型，第4节介绍了使用的数据集和生存分析模型中使用的主要特征。第5节提供了分析结果，并在第6节中对结果的解释和未来工作的方向进行了更深入的讨论。

2 相关工作

这项研究建立在游戏研究、网络科学和机器学习的长期研究链之上，其起源于管理大型多人在线游戏（MMOG）网络和服务器负载的努力。作为早期工作的代表，Chambers等人 [4] 最初通过挖掘客户端-服务器数据流来研究在线游戏的服务器负载。Tarng等人 [32] 和其他人扩展了这一领域，调查了人们为何离开游戏以及这与游戏时间的关系。早期对MMOG和其他在线游戏的时间模式的研究，通常一次研究一两个游戏，导致了最近的大规模调查，例如Sifa等人 [26] 的研究，他们在数千个游戏中发现了游戏时间与玩家流失之间的模式。游戏时间模式的发现，包括会话间隔、会话长度、总游戏时间等指标的重要性，与游戏行业中免费增值商业模式的增加采用相匹配，并引入了使用行为遥测预测玩家行为的想法。这反过来最近引入了对游戏中玩家行为进行预测分析的想法 [9, 17, 23, 27, 35, 39]，包括最近的生存分析 [34, 36]，以及通过这种类型的调查可以获得的见解。在这些主题的文献中，玩家离开被称为“流失”，离开的玩家被称为“流失者” [9]，采用了电信行业的术语。

在本节中，我们首先讨论了最近在分析和预测视频游戏流失方面所做的工作。强调了不同游戏类型之间的可用数据和玩家行为的差异，以及为解决这个问题使用的各种技术。然后介绍了在其他行业中使用生存分析技术进行流失预测，以展示其在非游戏环境中的成功应用，同时也指出其在玩家流失问题上的有限使用。

2.1 游戏中的流失分析

文献表明，行为和环境因素都是决定流失可能性的关键组成部分。对在线游戏中玩家流失的研究至少可以追溯到十年前，例如Feng等人 [7] 在Eve Online（一款科幻大型多人在线角色扮演游戏，MMORPG）中研究了这个问题，使用流量分析来检查2003-2006年游戏早期的数据。他们的结论之一是，玩家流失随时间增加，游戏会话之间的时间是“识别即将退出的玩家”（即流失）的可靠手段。Kawale等人 [14] 研究了其他玩家的社会影响对流失的影响。在MMORPG游戏Everquest II的背景下，发现通过结合玩家的会话长度（行为）和网络影响（环境）的分析，相比单独分析其中一个因素，流失预测的准确性显著提高。玩家的网络影响被建模为一个由两个分量组成的向量，一个是负面影响，另一个是正面影响，反映了玩家对游戏的倾向。他们发现，修改的扩散模型优于简单扩散模型和基于网络和参与特征的分类方法。然而，即使是最佳变体，其精度也刚刚超过50%，表明他们的方法还有很大的改进空间。玩家社交网络的重要性在SuperData [3] 进行的研究中得到了进一步的探讨。该调查发现，玩家倾向于成群放弃游戏，34%的流失玩家表示他们离开游戏是因为“朋友停止玩”。

Borbora等人 [1] 采用了基于数据分析和玩家动机理论的方法来预测可能流失的玩家。使用各种游戏玩法特征（如任务参与率）来训练决策函数，以确定玩家是否会流失。他们发现，基于理论的方法几乎与基于数据的方法一样准确，并声称前者更易于领域专家理解。他们还发现，单一分类算法可能无法识别所有可能的流失者。Runge等人 [23] 专门研究了社交游戏中的高价值玩家，其中高价值玩家被定义为所有付费玩家中排名前10%的玩家。他们评估了各种流失预测方法，包括使用隐马尔可夫模型和神经网络，使用来自两个游戏Diamond Dash和Monster World的数据集。他们发现，经过一些修改的单层隐含神经网络在预测可能流失的玩家方面表现最佳。他们随后在Monster World的背景下使用这一方法，识别出可能流失的玩家，并应用策略劝阻他们离开游戏，取得了一些可测量的成功。

2.2 其他行业中的流失

流失不仅是在线游戏的问题。客户留存被广泛认为比恢复流失客户的成本更低 [8]，Reichheld [20] 表示，在金融服务行业中，“客户留存率提高5%会带来超过25%的利润增长”。可以理解的是，关于流失预测和影响客户留存的因素，已经进行了广泛的研究和分析。在对在线赌博行业的研究中，Coussement和De Bock [5] 分析了行为和人口统计因素，使用随机森林模型和广义加性模型（GAM）对在线赌博行业进行了研究。根据对流失预测能力的排名，共有30个驱动因素（27个行为因素和3个人口统计因素），排名前三的变量是自上次投注以来的天数、自上次净亏损以来的天数以及相对于关系长度的投注会话数。

用于分析电信行业和信用卡提供等领域客户流失的统计模型包括逻辑回归和决策树分析，通常在遇到横截面数据时使用 [2]，[11]，[18]，[33]。在逻辑回归的情况下，通常选择一个任意阈值（特定于上下文）作为流失点，这导致一个二元响应变量，表示主体是否已流失。然后使用自变量来预测二元结果的概率。对于决策树分析，历史数据根据一组条件组织成层次结构，每个节点分配一个概率。Nie等人 [18] 比较了这两种技术在使用中国银行收集的信用卡数据预测流失方面的应用。分析的数据包括客户、卡片和风险信息以及交易活动。发现逻辑回归方法在性能上优于决策树算法。此外，用于客户留存建模的不同类别的统计模型通常根据数据类型分为“静态”和“动态”。静态模型应用于横截面数据，通常包括逻辑回归、线性回归和神经网络，而动态模型倾向于捕捉纵向数据，包括贝叶斯方法和生存分析 [40]。

2.3 流失预测的生存分析

在建模纵向数据时，生存分析是一种常见的方法，在许多行业中广泛使用。Lu [16] 在其关于“竞争激烈”的电信行业的研究中应用了生存分析技术。具体来说，该研究应用了参数回归模型来估计生存和风险函数，以提供有关客户流失率的信息，并识别高风险流失客户。Kaminski和Geisler [12] 使用生存分析来了解美国多所大学科学和工程副教授的留任情况，通过分析从最初雇用到离职的时间。此外，通过Zhang [40] 在零售银行客户数据上应用Cox比例风险模型，他发现增加客户服务使用、交叉购买、任期经验和复杂产品使用导致客户留存时间延长。

在游戏行业中应用混合效应Cox回归进行流失分析似乎不太常见，几乎没有公开可用的证据表明这一点。本文的目标是了解某些行为特征对玩家继续玩LoL的可能性的影响。具体来说，通过分析影响下一场比赛之间时间速率的因素，可以将与下一场比赛时间较长相关的行为特征作为潜在流失的领先指标。通过提供对比赛持续时间、连续比赛之间的时间和玩家技能对风险率影响的更深入了解，电子竞技公司将更好地了解如何为表现出这些特征并因此有流失风险的玩家引入有针对性的策略。鉴于Riot Games及其他电子竞技公司商业模式对通过游戏内购买产生的收入的依赖，必须尽早识别这些特征，以便采取必要的行动。

3 生存分析模型

在对纵向数据进行建模时，生存分析是一种常见的方法，广泛应用于许多行业。它用于预测事件发生前经过的时间，并基于潜在的影响特征进行预测。在传统的医学意义上，这个事件通常是反应、缓解或死亡。在我们的上下文中，类似的负面事件可能看起来是玩家的流失。然而，没有特定的时间点定义“流失事件”的发生，因此在我们的分析中，这个事件被反转；事件是玩家进行一场《英雄联盟》比赛。这意味着，如果玩家在从起始时间到当前时间间隔内没有进行游戏，则被认为是“存活”。因此，生存分析用于预测玩家再次进行比赛的时间长度。因此，如果预测玩家“存活”时间很长，那么很可能他们已经流失，并且不会返回，或者至少对游戏失去兴趣，暂时不会回来。

生存分析计算生存函数，该函数给出了主体在某个时间 $t$ 之后存活（未进行游戏）的概率： $S(t)=P(T\ge t)$。相反，风险函数用于给出在特定时间步长上事件（进行游戏）发生的概率，前提是它尚未发生，也称为瞬时失效率： $h(t)=-\frac{\partial }{\partial t}\log S(t)$。这两个量可以相互推导，因此它们是等价的。然而，本文重点关注风险函数，因为随着时间的推移，风险率的下降意味着玩家返回游戏的概率在下降。它也可以被视为玩家自主返回游戏的概率下降，因此可能需要开发者（Riot Games）的激励措施来促使其返回。

我们首先使用 Kaplan-Meier 估计器在群体水平上对生存函数进行建模。然后，我们使用标准 Cox 回归模型和混合效应回归模型研究行为变量的影响。使用的所有模型将在接下来的部分中介绍。

3.1 Kaplan-Meier 估计器

生存分析通常面临与数据相关的困难。例如，一些个体在研究期间没有经历“事件”，因此不知道他们在经历事件之前经过了多长时间，或者是否经历了事件。此外，一些个体可能决定在研究结束前退出。这些类型的未知数据被称为截尾数据。尽管存在这些困难，计算随时间推移的生存概率的最简单方法是 Kaplan-Meier 估计器 [13]。生存概率根据在时间 $t$ 之后存活的观测数除以给定时间间隔内风险集中的总观测数来估计。Hosmer Jr 和 Lemeshow [10] 用以下公式总结了这一点：

$$S(t)=\prod _{t_i\le t}\left(\frac{n_i-d_i}{n_i}\right),(1)$$

其中 $n_i$ 表示风险事件的观测数，$d_i$ 表示经历事件的观测数。

Kaplan-Meier 估计的主要限制是它在群体水平上建模生存。相反，理想情况下，我们希望将生存建模为某些特征（例如行为特征）的函数。在下一节中介绍的标准 Cox 回归模型解决了这一需求。

3.2 标准 Cox 回归模型

标准 Cox 回归模型 [6] 可以用来探索特定特征与经历某些定义事件的速率之间的关系。该模型假设特征的函数形式（参数化），而对生存时间没有分布假设（非参数化）。这使得该模型相对于其他需要对响应变量进行分布条件假设的统计模型具有优势。

该模型假设风险函数具有以下形式：

$$h(t)=h_0(t)e^{{\beta }^{T}x},(2)$$

其中 $h_0(t)$ 表示时间 $t$ 的基线风险函数（即当所有解释变量为零时的风险函数），$x$ 是解释变量的向量，$\beta$ 是系数的向量。这个模型使得可以检查多个独立变量对生存的影响。

Cox 回归模型的关键假设是比例风险假设，即每个个体间比赛观察的风险函数是任何其他间比赛时间的风险函数的倍数。也就是说，所有玩家将具有几个假定具有相同比例形状的风险函数，从而导致特征在时间上对风险率产生恒定的影响。

鉴于我们分析的数据结构，其中每个玩家的连续比赛被记录下来，独立性条件可能会因为个体玩家连续比赛之间的内在相关性而被违反。如果在不考虑玩家内部可能依赖性的情况下拟合 Cox 回归模型，可能会导致不准确和误导性的结果。

Cox [6] 提出了一种通过最大化部分似然函数来估计标准 Cox 回归模型参数的方法。本文不涉及这一内容，因为它超出了本文的范围。

3.3 混合效应 Cox 回归模型

上述标准 Cox 回归模型的扩展是混合效应 Cox 回归模型 [6]，其给出了第 $i$ 个簇中第 $j$ 个观察值的风险率：

$$\lambda (t{)}_{ij}={\lambda }_0(t)e^{\beta x_{ij}+b_i{z}_{ij}},(3)$$

其中 ${\lambda }_0(t)$ 是基线风险函数，$x_{ij}$ 是包含固定效应变量的向量，$\beta$ 是包含固定效应系数的向量，$z_{ij}$ 是包含随机效应变量的向量，$b_i$ 是第 $i$ 个簇的随机效应，从包含随机效应的向量中抽取，假设其服从均值为 0 的正态分布，协方差矩阵为 $\Sigma$。

该模型通过增加一个随机效应成分来解释玩家时间之间的依赖性。模型中“混合”一词指的是固定效应和随机效应的组合。这允许群体中的异质性，其中给定个体的聚类事件时间之间存在依赖性。通过引入这个随机项，个体玩家如果具有较高的敏感性，将会有增加（或减少）的风险率。

混合效应 Cox 回归模型通过要求每个主体仅属于一个簇来引入一个额外的假设。我们的数据满足这一假设，其中每次比赛（主体）直到下一场比赛的时间是唯一的，并且属于一个个体玩家（簇）。

Ripatti 和 Palmgren [22] 介绍了一种使用惩罚部分似然技术来对混合效应 Cox 回归模型进行参数估计的广义方法。本文不涉及这一内容，因为它超出了本文的范围。

4 数据集和特征

我们分析历史数据以建模和预测玩家退出游戏的概率。我们的分析基于玩家的行为特征，即最近平均比赛时长（RAMD）和最近平均比赛间隔时间（RATBM），这两个特征都是在最后一次事件前的90天内计算的。我们还使用最高赛季段位（HAST）作为玩家技能水平的代理变量。我们感兴趣的响应变量是到下一场比赛的时间（TUNM）。

我们的分析基于从《英雄联盟》API2 收集的数据。首先，我们从2015年参加公开活动的42,006名玩家中随机抽取了1000名来自大洋洲地区的玩家。对于每个玩家，我们收集了2014年5月至2016年9月之间的比赛数据。由于数据限制，我们只能下载201名玩家的数据，总计7,842场比赛。然而，这仍然提供了大量的数据点。

感兴趣变量的分布如图1、图2（解释变量）和图3（响应变量）所示。

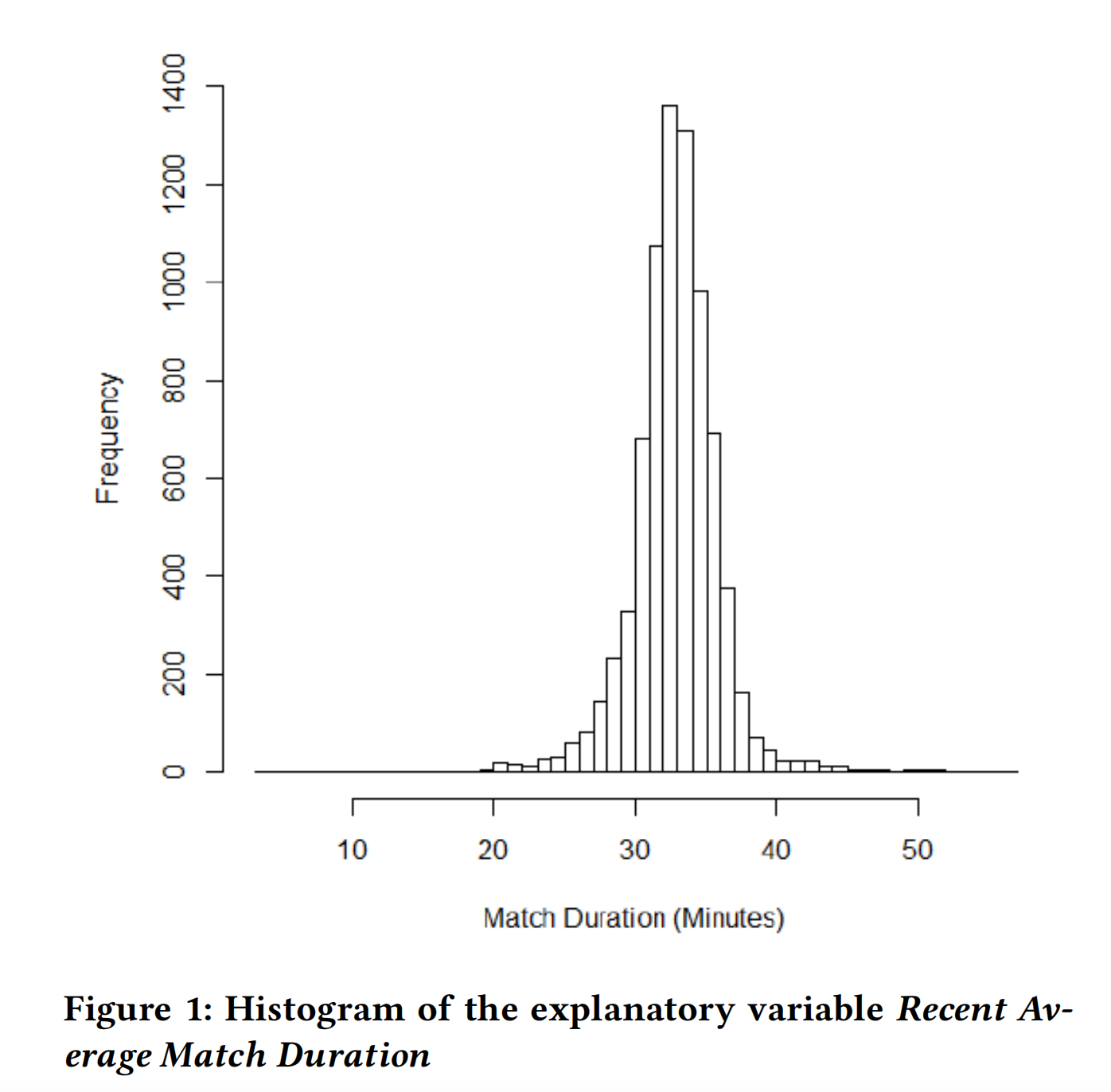
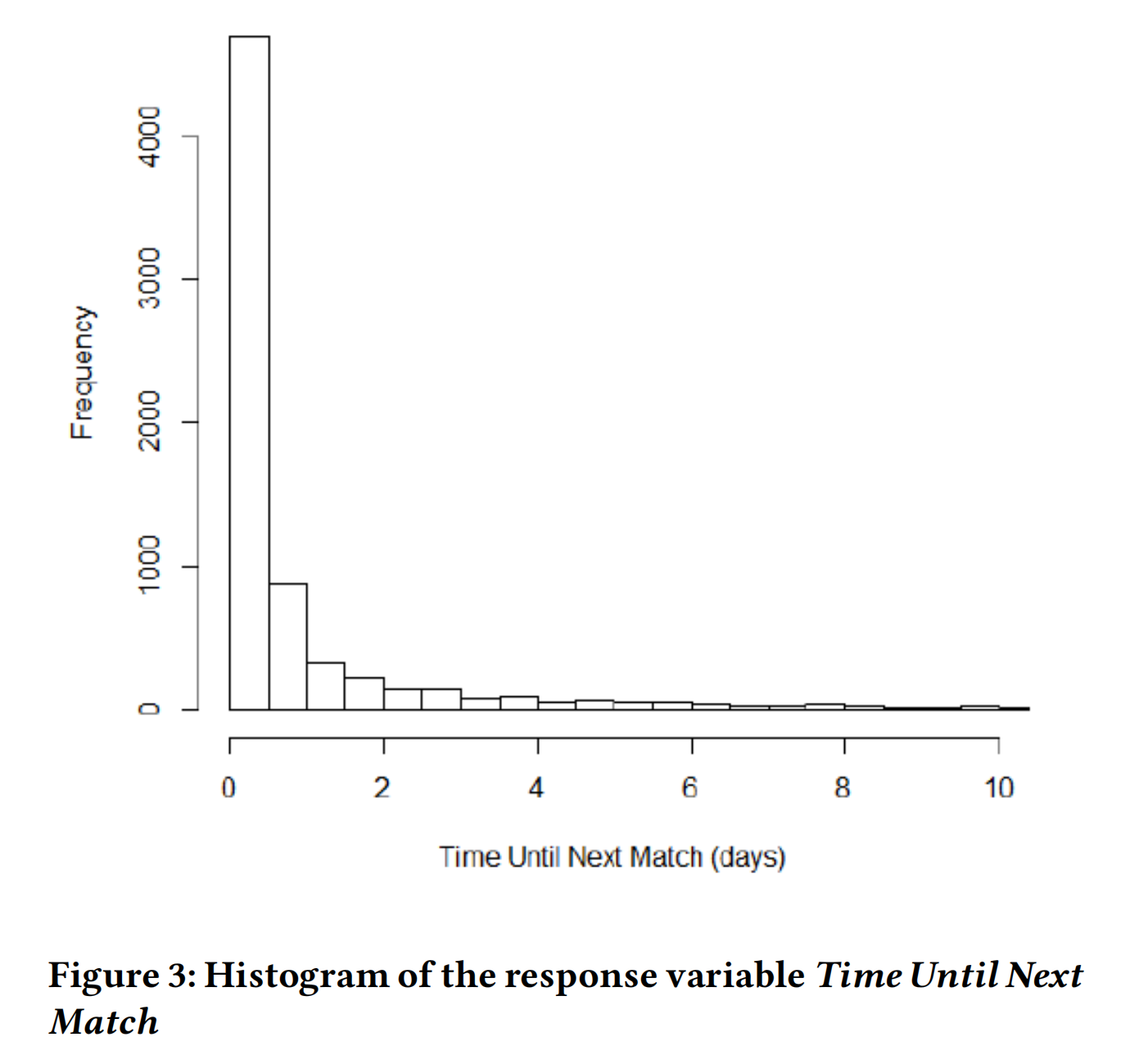
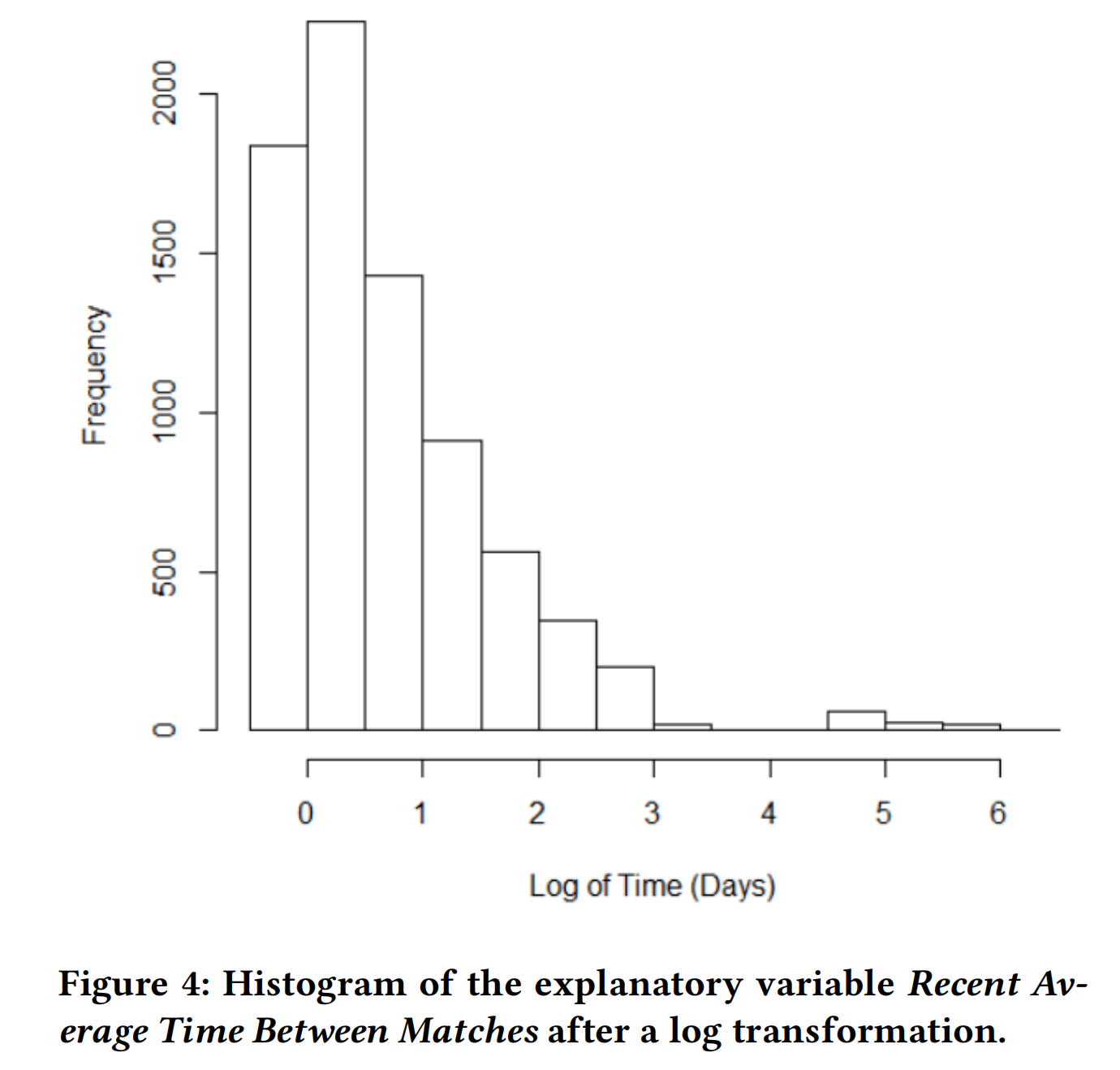
变量最近平均比赛时长大致呈正态分布。另一方面，变量最近平均比赛间隔时间严重偏斜，因此我们应用了对数变换来缓解这个问题。图4显示了变换后变量的分布。响应变量严重偏斜（下四分位数为45分钟，中位数约为1小时38分钟，上四分位数几乎为2年）并且有一些极端的异常值。我们排除了2个观察值，这些观察值中玩家在12个月内没有玩游戏，然后只玩了一场比赛。尽管删除了这些异常值，数据仍然表现出严重的右偏。然而，对于生存分析，响应变量没有强加分布假设，因此不会删除更多的数据点。

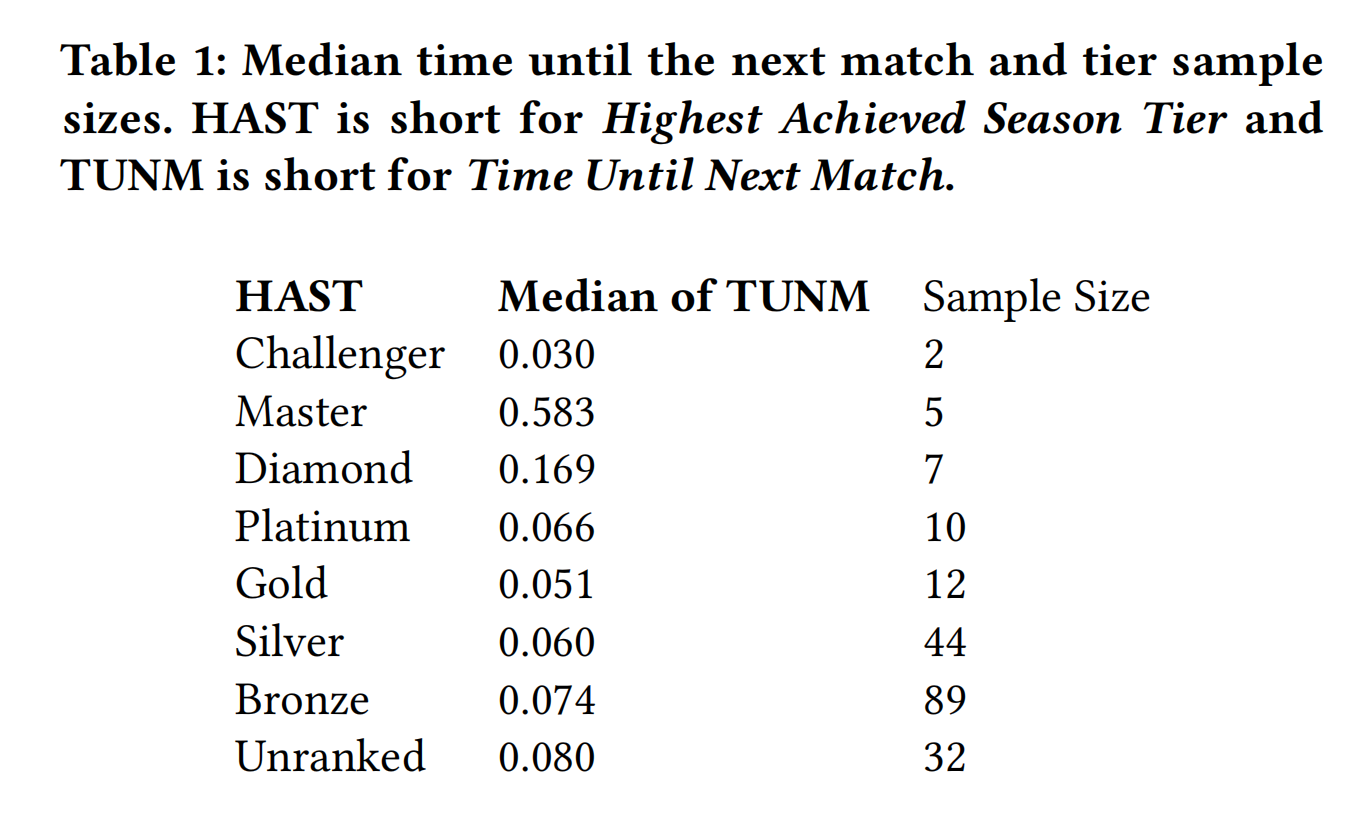
每个最高赛季段位的到下一场比赛的时间的中位数值和样本量如下表1所示。排序段位和时间之间似乎没有明显的关联或趋势。然而，各类别之间的样本量差异很大，高段位玩家的样本量明显较少，这可能会影响结果的可靠性。

5 结果

在本节中，我们展示了对《英雄联盟》数据进行分析的结果。Kaplan-Meier 和标准/混合效应 Cox 回归模型的结果将在接下来的章节中报告。

5.1 Kaplan-Meier

包含95%置信区间（虚线）的响应变量的估计 Kaplan-Meier 生存函数如图5所示。Kaplan-Meier 估计器是一种非参数方法，用于估计超出感兴趣事件的生存概率，并考虑了删失的事件时间数据。图5描绘了在最初的急剧下降后，生存概率随时间的下降率逐渐减缓。这表明随着比赛间隔时间的增加，连续比赛的概率减少。曲线在第100天左右开始趋于平稳，表明到下一场比赛时间超过100天的玩家返回游戏的概率非常低。

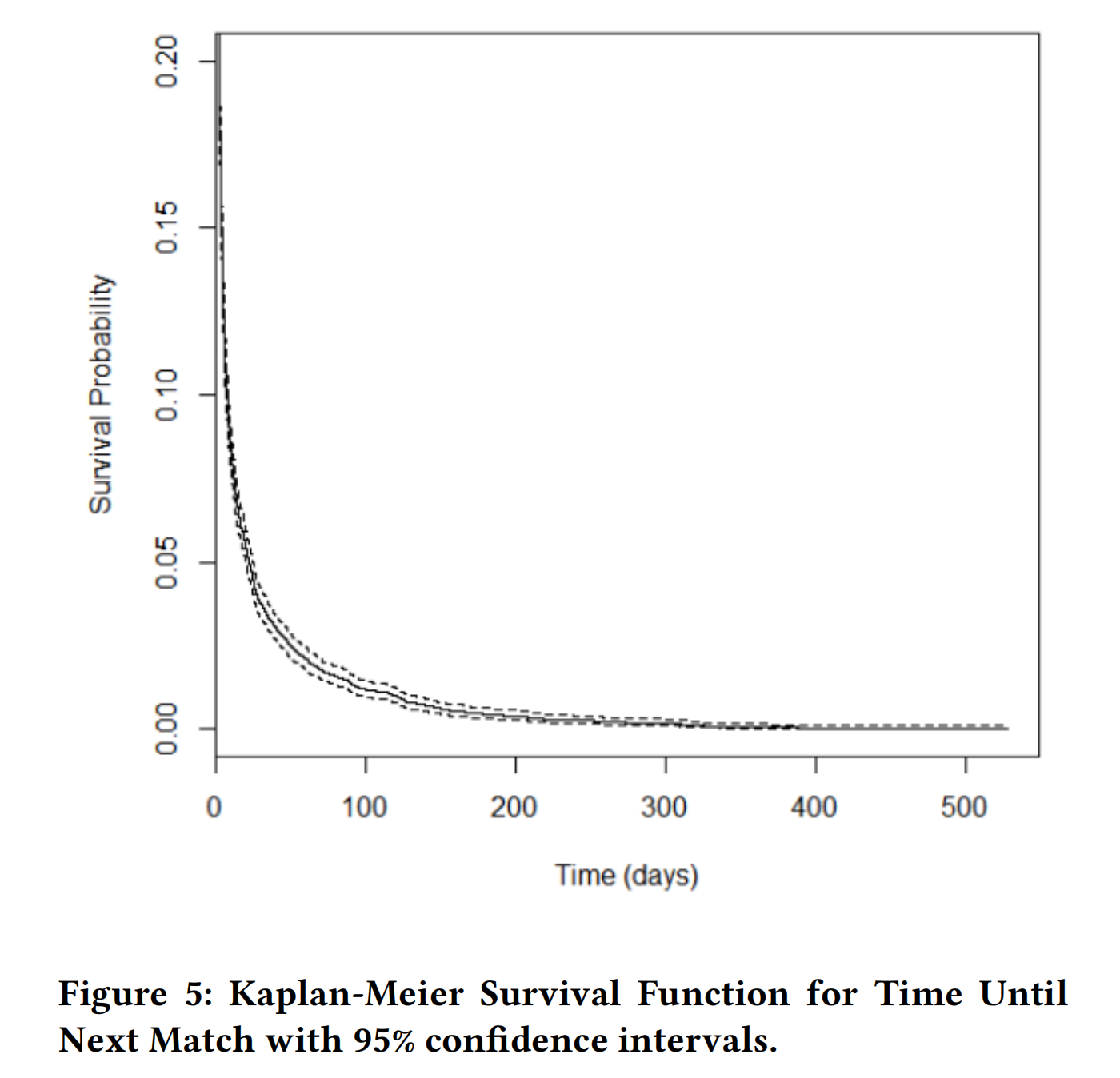
鉴于最初的急剧下降，生存函数在图6中再次绘制，时间范围为6小时（0.25天），因为58%的观察值低于此阈值。可以更容易地观察到，观察值包含的比赛尚未进行的概率在大约1小时12分钟（0.05天）后下降到约50%。该图中的初始平台代表了所有玩家仍在进行与之前事件相关的比赛的时间。

5.2 标准 Cox 回归模型

我们拟合了一个标准 Cox 回归模型，包括两个连续变量和一个包含七个段位的分类变量，相对于挑战者段位提供风险比。该模型将所有观察值单独处理，而不考虑玩家比赛的聚类。

如前所述，比例风险假设要求所有特征的风险函数在时间上必须成比例。我们运行了缩放的 Schoenfeld [24] 残差与时间之间的 Pearson 积矩相关性，以验证数据中假设的成立。我们发现最近平均比赛时长（$p<0.001$）和最近平均比赛间隔时间（$p=0.030$）的 p 值较小，提供了违反比例风险的证据。对于分类变量最高赛季段位的检验结果不显著（$0.627\le p\le 0.899$），因此满足比例风险假设。全局检验具有较大的卡方值，表明整体模型违反了比例风险假设（$p<0.001$）。

考虑到关于数据的一些假设被违反，标准 Cox 回归模型的输出如表2所示。风险比小于1的值与到下一场比赛时间较长相关。

5.3 混合效应 Cox 回归模型

我们拟合了一个混合效应 Cox 回归模型，将玩家ID作为随机效应变量，以解释簇内依赖性；即玩家不同时间之间的依赖性。回归的输出如表3所示。

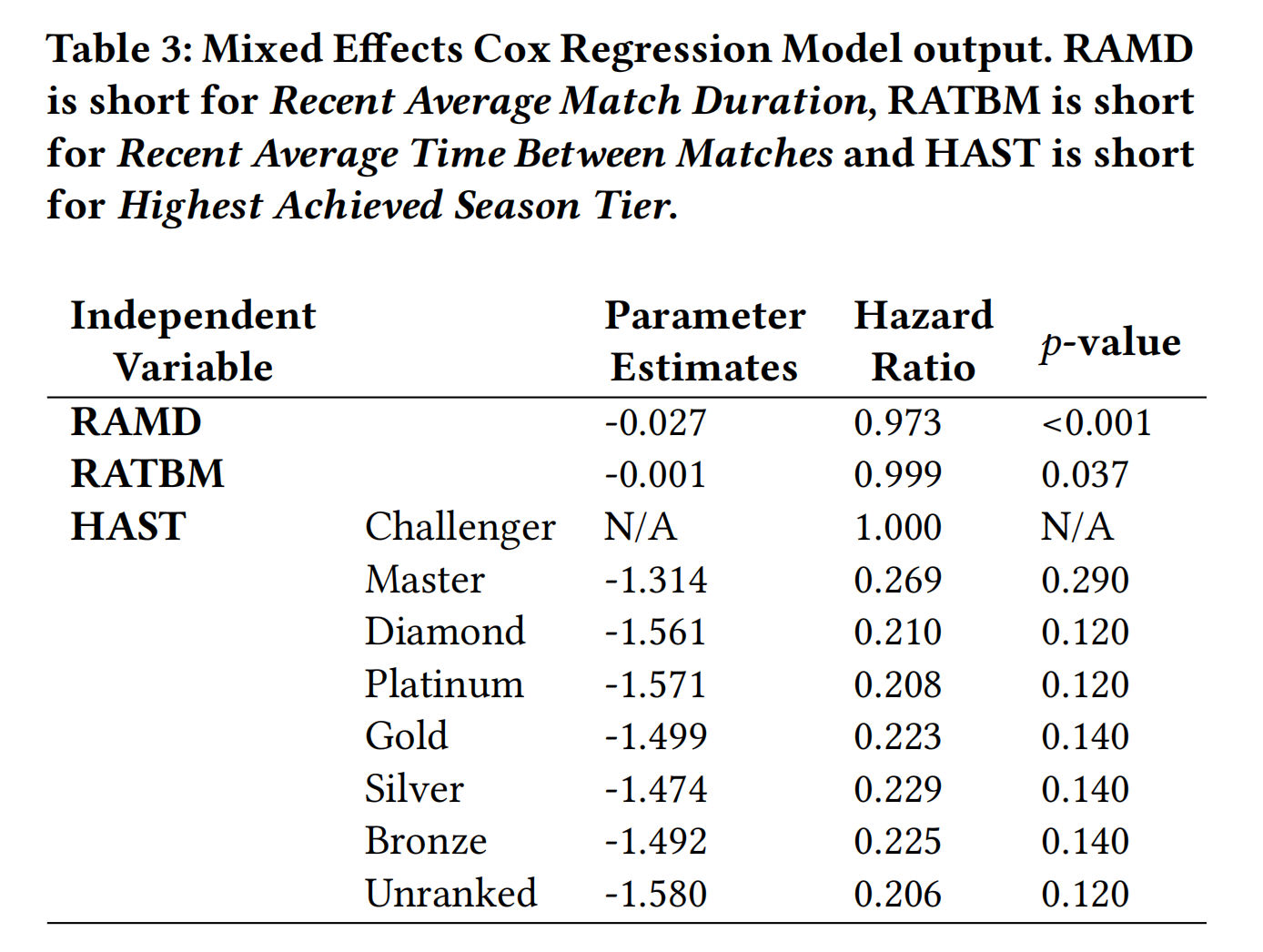
风险比小于1的值与到下一场比赛时间较长相关。输出显示最近平均比赛时长具有显著影响（$p<0.001$）。风险比为0.973表明最近平均比赛时长每增加1分钟，风险率降低2.7%（$1-e^{1\cdot -0.027}\approx 0.027$）。同样，最近平均比赛时长增加15分钟，相当于到下一场比赛时间的降低33%（$1-e^{15\cdot -0.027}\approx 0.333$）。因此，随着玩家比赛时长的增加，到下一场比赛的时间减少。

最近平均比赛间隔时间也发现有显著影响（$p=0.037$）。虽然该特征的显著性不如比赛时长特征强，但风险比表明最近平均比赛间隔时间每增加一天，风险率降低0.1%（$1-e^{1\cdot -0.001}\approx 0.001$）。

就最高赛季段位而言，所有段位在5%水平上均不显著（所有 $p\ge 0.12$）。

5.4 模型比较

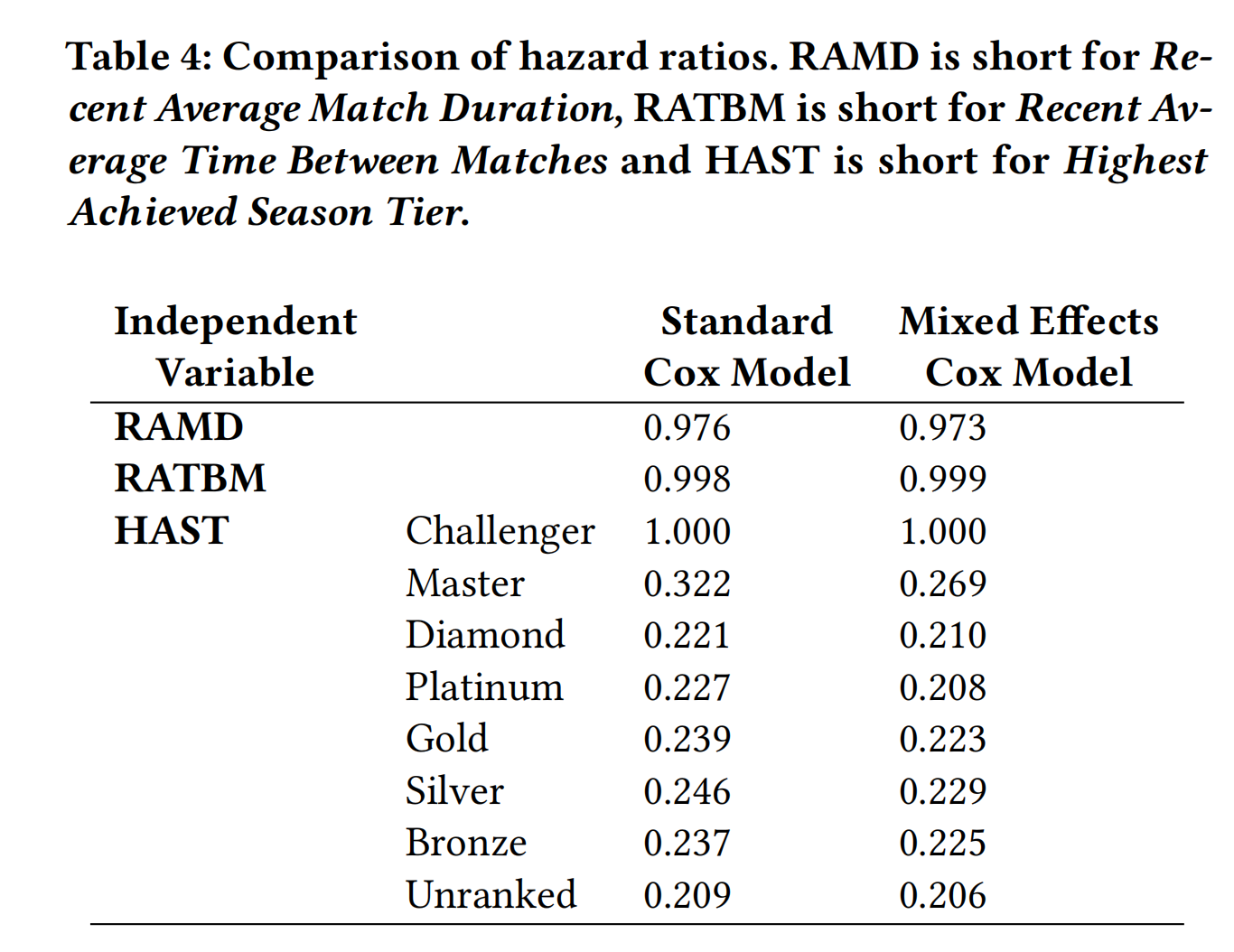
标准 Cox 回归模型和混合效应 Cox 回归模型的风险比比较如表4所示。可以看出，考虑和不考虑随机效应的比率相对稳定。这表明在整体模型中拟合随机项影响较小。

6 讨论

本研究使用混合效应 Cox 回归模型量化了玩家行为和技能对到下一场比赛时间率的影响。发现随着游戏时间的增加，到下一场比赛发生的时间率下降。这可能表明玩家经历了一场更具挑战性的比赛。由于缺乏指示玩家是否赢得或输掉特定比赛的变量，很难将较长的比赛时间归因于玩家之间的技能差异，或者是长时间的“输”或长时间的“赢”对这种下降的影响。随着时间的推移，玩家可能会感到沮丧或有些挫败，结果是他们不太愿意立即重新开始游戏。因此，提供一个指示“赢”或“输”的变量可能会改善模型拟合和结果解释。

同样，发现增加连续比赛之间的平均时间与下一场比赛的时间段较长相关。通常，人们会预期那些对游戏越来越不感兴趣的个体，往往会在后续比赛之间有较长的间隔。同样，如果没有关于玩家年龄或玩家外部环境等方面的更多信息，很难得出结论。这些因素可能会提供更多关于个体行为特定情况的信息。

未发现玩家之前最高赛季段位（作为玩家技能水平的代理变量）与比赛率相关。这可能是因为 Riot Games 实施了针对不活跃行为的规则。例如，挑战者段位的玩家（最高排名）在10天不活跃后会被降级。另一个激励机制是联盟积分，在28天不活跃期后，白金、钻石、大师和挑战者段位的玩家会失去积分。预计玩家技能水平会对到下一场比赛的时间产生一定影响。然而，这个变量对比赛的可能性没有显著贡献。需要注意的是，由于高段位样本量较小，如第4节所述，这一结论可能存在偏差。

选定的观察期包括2014年5月到2016年9月的比赛。时间段的长度以及选定的观察期的变化可能会影响结果。Riot Games 不断尝试通过对游戏玩法和角色进行更改来改进游戏。在不同时期进行生存分析，例如在主要补丁或角色重做之后，可能会提供更深入的玩家流失影响的见解。

此外，鉴于本研究涉及在线产品，技术的变化可能会影响用户体验。最佳实践是继续使用最新的 LoL 玩家数据，以保持结果的相关性。新游戏不断发布，这带来了未来可能发布一款游戏取代 LoL 并导致大量玩家迁移离开这款 MOBA 游戏的风险。

通过整合玩家消费水平和购买频率等数据，可能会改进分析。Coussement 等人 [5] 在其对在线赌博行业流失的研究中整合了货币因素。发现包括前一周下注次数、前一个月下注次数和总下注金额在内的因素是流失的重要驱动因素。将这些因素纳入保留分析，将更好地帮助 Riot Games 通过分析有更高倾向进行游戏内购买的玩家行为来针对接近流失的玩家。请注意，这些数据目前在 API 中不可用，需要从其他地方获取。

7 结论与未来工作

如第1节介绍和第2节讨论的那样，本分析的动机来自于 Riot Games 采用的商业模式，该模式高度依赖于客户保留，并进一步为游戏研究中关注玩家活动行为模式的广泛主题做出贡献。LoL 不同于需要订阅费或下载前费用的在线游戏。因此，进行这项研究的理论基础是玩家忠诚度在一个主要通过游戏内购买产生收入的游戏中的重要性。

本文关于行为因素的发现与之前的研究一致。如第2节所述，最近的研究发现了支持玩家行为与流失之间关联的证据 [5], [14]。包括平均比赛时长和连续比赛之间的平均时间在内的玩家行为特征被发现是影响到下一场比赛时间率的重要因素。本研究提供了玩家行为与比赛可能性之间关联的证据。更具体地说，本研究应用了包括混合效应 Cox 回归模型在内的生存分析技术，结果显示随着平均比赛时长的缩短，到玩家下一场比赛的时间率增加。同样，结果表明，连续比赛之间的时间段越长，与到玩家下一场比赛的时间率的下降相关。这种分析以及越来越复杂的方法将继续为理解和洞察玩家流失的指标做出贡献。鉴于持续的玩家购买是主要收入来源，这些见解将变得越来越有价值。

在未来的工作中，我们计划将这项研究扩展到 LoL 服务器所在的不同地区。这将消除由于仅包含大洋洲地区玩家而导致的人口偏差。此外，将这项工作扩展到不同地区将允许比较不同地区的风险率，这可能为基于位置的玩家流失影响提供有用的见解。我们还计划在不同时间点（即补丁或角色重做后）进行生存分析，以研究重大变化如何影响玩家流失。这种分析可能为预测玩家流失提供见解，或者用于指导游戏的未来添加和更改。

致谢

作者感谢 ARC LP130100743 的支持。此外，本工作得到了由 EPSRC/AHRC/InnovateUK 共同资助的数字创意实验室（Digital Creativity Labs）资助，资助编号为 EP/M023265/1。

REFERENCES

[1] Zoheb Borbora, Jaideep Srivastava, Kuo-Wei Hsu, and Dmitri Williams. 2011.
Churn prediction in mmorpgs using player motivation theories and an ensemble
approach. In Privacy, Security, Risk and Trust (PASSAT) and 2011 IEEE Third Inernational Conference on Social Computing (SocialCom), 2011 IEEE Third International
Conference on. IEEE, 157–164.

[2] Ionut Brandusoiu and Gavril Toderean. 2013. Churn prediction modeling in
mobile telecommunications industry using decision trees. Journal of Computer
Science and Control Systems 6, 1 (2013), 14.

[3] James Brightman. 2016. League of Legends generates 150m
a month - SuperData. http://www.gamesindustry.biz/articles/
2016-06-09-league-of-legends-generates-usd150m-a-month-superdata.
(2016).

[4] Chris Chambers, Wu-chang Feng, Sambit Sahu, and Debanjan Saha. 2005.
Measurement-based characterization of a collection of on-line games. In Proceedings of the 5th ACM SIGCOMM conference on Internet Measurement. USENIX
Association, 1–1.

[5] Kristof Coussement and Koen W De Bock. 2013. Customer churn prediction in
the online gambling industry: The beneficial effect of ensemble learning. Journal
of Business Research 66, 9 (2013), 1629–1636.

[6] David R Cox. 1992. Regression models and life-tables. In Breakthroughs in
statistics. Springer, 527–541.

[7] Wu-chang Feng, David Brandt, and Debanjan Saha. 2007. A long-term study
of a popular MMORPG. In Proceedings of the 6th ACM SIGCOMM Workshop on
Network and System Support for Games. ACM, 19–24.

[8] John Hadden, Ashutosh Tiwari, Rajkumar Roy, and Dymitr Ruta. 2007. Computer assisted customer churn management: State-of-the-art and future trends.
Computers & Operations Research 34, 10 (2007), 2902–2917.

[9] Fabian Hadiji, Rafet Sifa, Anders Drachen, Christian Thurau, Kristian Kersting, and Christian Bauckhage. 2014. Predicting player churn in the wild. In
Computational intelligence and games (CIG), 2014 IEEE conference on. IEEE, 1–8.

[10] David W Hosmer Jr and Stanley Lemeshow. 1999. Applied survival analysis:
regression modelling of time to event data (1999). Eur Orthodontic Soc (1999),
561–2.

[11] Shin-Yuan Hung, David C Yen, and Hsiu-Yu Wang. 2006. Applying data mining
to telecom churn management. Expert Systems with Applications 31, 3 (2006),
515–524.

[12] Deborah Kaminski and Cheryl Geisler. 2012. Survival analysis of faculty retention
in science and engineering by gender. Science 335, 6070 (2012), 864–866.

[13] Edward L Kaplan and Paul Meier. 1958. Nonparametric estimation from incomplete observations. Journal of the American statistical association 53, 282 (1958),
457–481.

[14] Jaya Kawale, Aditya Pal, and Jaideep Srivastava. 2009. Churn prediction in
MMORPGs: A social influence based approach. In Computational Science and
Engineering, 2009. CSE’09. International Conference on, Vol. 4. IEEE, 423–428.

[15] P Kollar. 2017. The Past, Present and Future of League of Legends Studio Riot
Games, Polygon Platform, 2016. http://www.polygon.com/2016/9/13/12891656/
the-past-present-and-future-of-league-of-legends-studio-riot-games. (2017).

[16] Junxiang Lu. 2002. Predicting customer churn in the telecommunications
industry—-An application of survival analysis modeling using SAS. SAS User
Group International (SUGI27) Online Proceedings (2002), 114–27.

[17] M. Milosevic, N. Zivic, and I. Andjelkovic. 2017. Early churn prediction with
personalized targeting in mobile social games. Expert Systems with Applications
(2017).

[18] Guangli Nie, Wei Rowe, Lingling Zhang, Yingjie Tian, and Yong Shi. 2011. Credit
card churn forecasting by logistic regression and decision tree. Expert Systems
with Applications 38, 12 (2011), 15273–15285.

[19] Noppon Prakannoppakun and Sukree Sinthupinyo. 2016. Skill rating method in
multiplayer online battle arena. In Electronics, Computers and Artificial Intelligence
(ECAI), 2016 8th International Conference on. IEEE, 1–6.

[20] Fred Reichheld. 2001. Prescription for cutting costs. Bain & Company. Boston:
Harvard Business School Publishing (2001). http://www.bain.com/IMages/BB_
Prescription_cutting_costs.pdf

[21] François Rioult, Jean-Philippe Métivier, Boris Helleu, Nicolas Scelles, and
Christophe Durand. 2014. Mining tracks of competitive video games. AASRI
Procedia 8 (2014), 82–87.

[22] Samuli Ripatti and Juni Palmgren. 2000. Estimation of multivariate frailty models
using penalized partial likelihood. Biometrics 56, 4 (2000), 1016–1022.

[23] Julian Runge, Peng Gao, Florent Garcin, and Boi Faltings. 2014. Churn prediction
for high-value players in casual social games. In Computational Intelligence and Games (CIG), 2014 IEEE Conference on. IEEE, 1–8.

[24] David Schoenfeld. 1982. Partial residuals for the proportional hazards regression
model. Biometrika 69, 1 (1982), 239–241.

[25] Matthias Schubert, Anders Drachen, and Tobias Mahlmann. 2016. Esports analytics through encounter detection. In Proceedings of the MIT Sloan Sports Analytics
Conference.

[26] Rafet Sifa, Christian Bauckhage, and Anders Drachen. 2014. The Playtime Principle: Large-scale cross-games interest modeling. In Computational Intelligence
and Games (CIG), 2014 IEEE Conference on. IEEE, 1–8.

[27] R. Sifa, F. Hadiji, J. Runge, A. Drachen, K. Kersting, and C. Bauckhage. 2015.
Predicting Purchase Decisions in Mobile Free-to-Play Games. In Proc. of AAAI
AIIDE.

[28] Adam Summerville, Michael Cook, and Ben Steenhuisen. 2016. Draft-Analysis
of the Ancients: Predicting Draft Picks in DotA 2 using Machine Learning. In
Twelfth Artificial Intelligence and Interactive Digital Entertainment Conference.

[29] Superdata. 2016. 2016 MMO and MOBA Games Market. (2016). https://www.
superdataresearch.com/market-data/mmo-market/

[30] Superdata. 2016. Year in Review, December 2016. (2016). https://www.
superdataresearch.com/market-data/market-brief-year-in-review/

[31] Superdata Research. 2017. European Esports Conference Brief
(http://strivesponsorship.com/wp-content/ uploads/2017/04/Superdata-2017-
esports-market-brief.pdf). (2017). http://strivesponsorship.com/wp-content/
uploads/2017/04/Superdata-2017-esports-market-brief.pdf

[32] Pin-Yun Tarng, Kuan-Ta Chen, and Polly Huang. 2009. On prophesying online
gamer departure. In Proceedings of the 8th Annual Workshop on Network and
Systems Support for Games. IEEE Press, 16.

[33] Thanasis Vafeiadis, Konstantinos I Diamantaras, George Sarigiannidis, and K Ch
Chatzisavvas. 2015. A comparison of machine learning techniques for customer
churn prediction. Simulation Modelling Practice and Theory 55 (2015), 1–9.

[34] Markus Viljanen, Antti Airola, Jukka Heikkonen, and Tapio Pahikkala. 2017.
Playtime Measurement with Survival Analysis. arXiv preprint arXiv:1701.02359
(2017).

[35] Markus Viljanen, Antti Airola, Anne-Maarit Majanoja, Jukka Heikkonen, and
Tapio Pahikkala. 2017. Measuring Player Retention and Monetization using the
Mean Cumulative Function. arXiv preprint arXiv:1709.06737 (2017).

[36] Markus Viljanen, Antti Airola, Tapio Pahikkala, and Jukka Heikkonen. 2016.
Modelling user retention in mobile games. In Computational Intelligence and
Games (CIG), 2016 IEEE Conference on. IEEE, 1–8.

[37] Huiwen Wang, Bang Xia, and Zhe Chen. 2015. Cultural Difference on Team
Performance Between Chinese and Americans in Multiplayer Online Battle Arena
Games. Springer International Publishing, Cham, 374–383. https://doi.org/10.
1007/978-3-319-20934-0_35

[38] M. Wu, S. Xiong, and H. Iida. 2016. Fairness mechanism in multiplayer online
battle arena games. In 2016 3rd International Conference on Systems and Informatics
(ICSAI). 387–392. https://doi.org/10.1109/ICSAI.2016.7810986

[39] Hanting Xie, Sam Devlin, Daniel Kudenko, and Peter Cowling. 2015. Predicting
Player Disengagement and First Purchase with Event-frequency Based Data
Representation. In Proc. of CIG.

[40] Hong Zhang. 2008. Customer retention in the financial industry: An application of
survival analysis. Ph.D. Dissertation. Purdue University

本文由mdnice多平台发布

原文地址：https://blog.csdn.net/hahoo2009/article/details/144070146

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！