Matlab|基于粒子群算法优化Kmeans聚类的居民用电行为分析

 

目录

 

主要内容   

  部分代码   

  结果一览   

下载链接

---

主要内容   

在我们研究电力系统优化调度模型的过程中，由于每天负荷和分布式电源出力随机性和不确定性，可能会优化出很多的结果，但是经济调度模型试图做到通用策略，同样的策略能够适用于不同的负荷和分布式电源特征，为了做到这一点，就出现随机优化、鲁棒优化等等方法，当然我们也可以像这个程序一样，对负荷进行聚类分析，对归纳得到的共性负荷特征再进行优化调度分析，模型的说服力会大大增强。

常见的聚类算法包括kmeans聚类、层次聚类、DBSCAN聚类和谱聚类等，本模型采用的是kmean聚类，传统kmeans算法流程如下：

1. 初始化：

• 选择聚类的数量K。
• 随机选择K个数据点作为初始聚类中心。

1. 分配数据点到最近的聚类中心：

• 对于数据集中的每个点，计算它与K个聚类中心之间的距离。
• 将每个点分配到距离最近的聚类中心，形成K个簇。

1. 重新计算聚类中心：

• 对于每个簇，计算簇内所有数据点的均值，这个均值就是新的聚类中心。

1. 判断收敛：

• 如果新的聚类中心与旧的聚类中心相同，或者达到预设的迭代次数，或者簇的成员不再发生变化，则算法收敛，结束流程。
• 否则，返回步骤2继续迭代。

反复的迭代过程导致kmeans算法具有迭代时间长和性能不稳定等问题，为了解决该问题，通过粒子群算法和聚类算法的结合有效提升算法效能，具体流程步骤为：

  部分代码   

function Error=PredoKMeans(Index,X,Replicate)
%%  Kmeans聚类算法
%  Index为从X中随机抽取的中心样本序号
​
%  行数
N=size(X,1);
M=size(X,2);
%  聚类情况
Position=zeros(N,1);
H=length(Index);
%  选择样本的中心
Index=floor(Index);
Center=X(Index,:);
%  总重构误差
for i=1:Replicate
    Error=0;
    for j=1:N
        if M==1
            Distance=(repmat(X(j,:),H,1)-Center).^2;
        elseif M>1
            Distance=sum((repmat(X(j,:),H,1)-Center).^2,2);
        end
        %  选择最小的距离
        [Dis,Index]=min(Distance);
        Position(j)=Index;
        Error=Error+Dis;
    end
%     %  更新聚类中心
%     for j=1:H
%         Center(j,:)=mean(X(Position==j,:));
%     end
end

  结果一览   

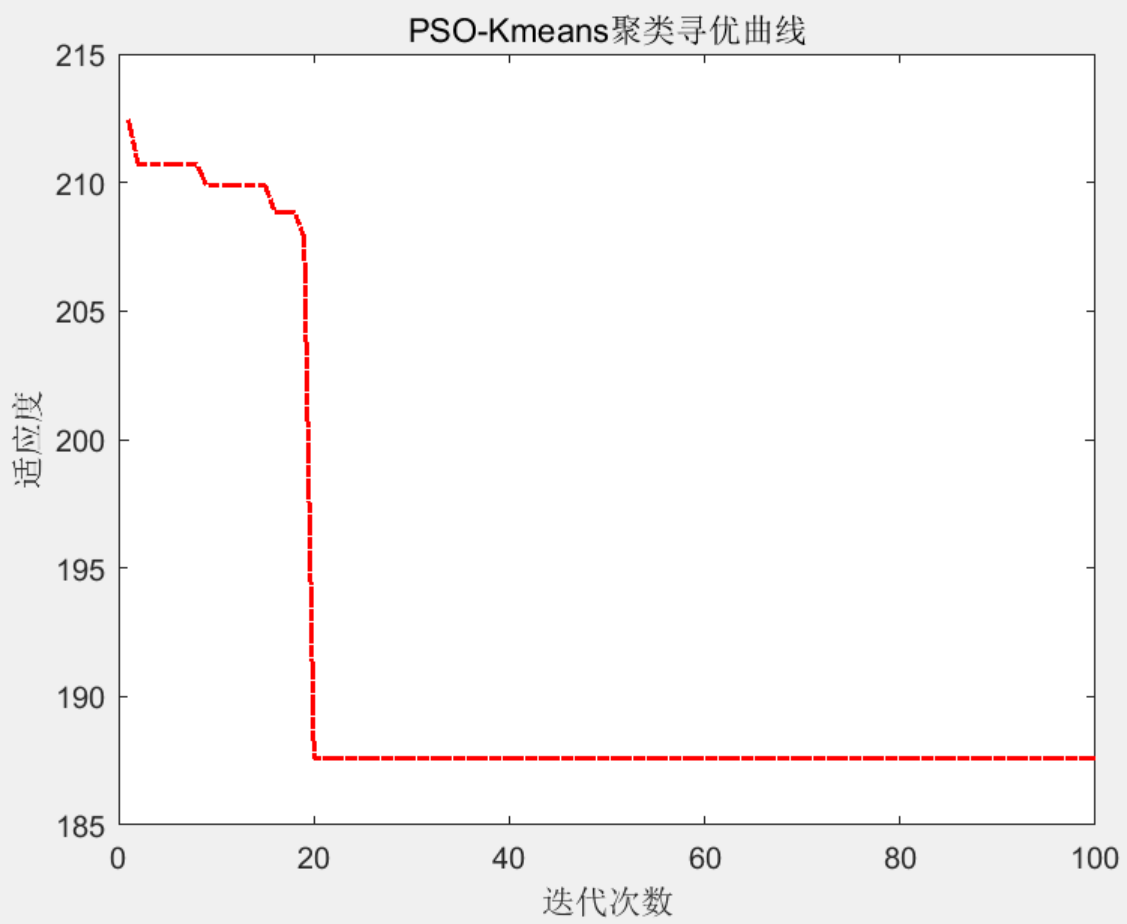
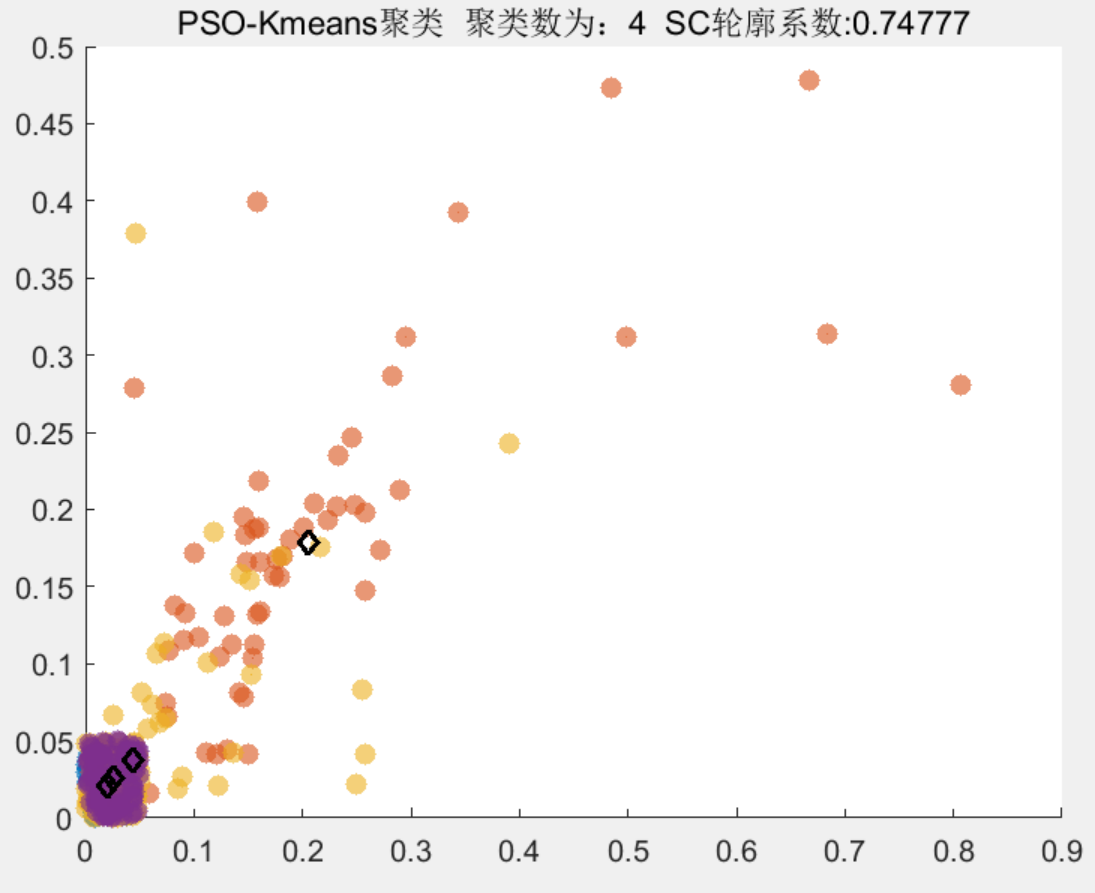
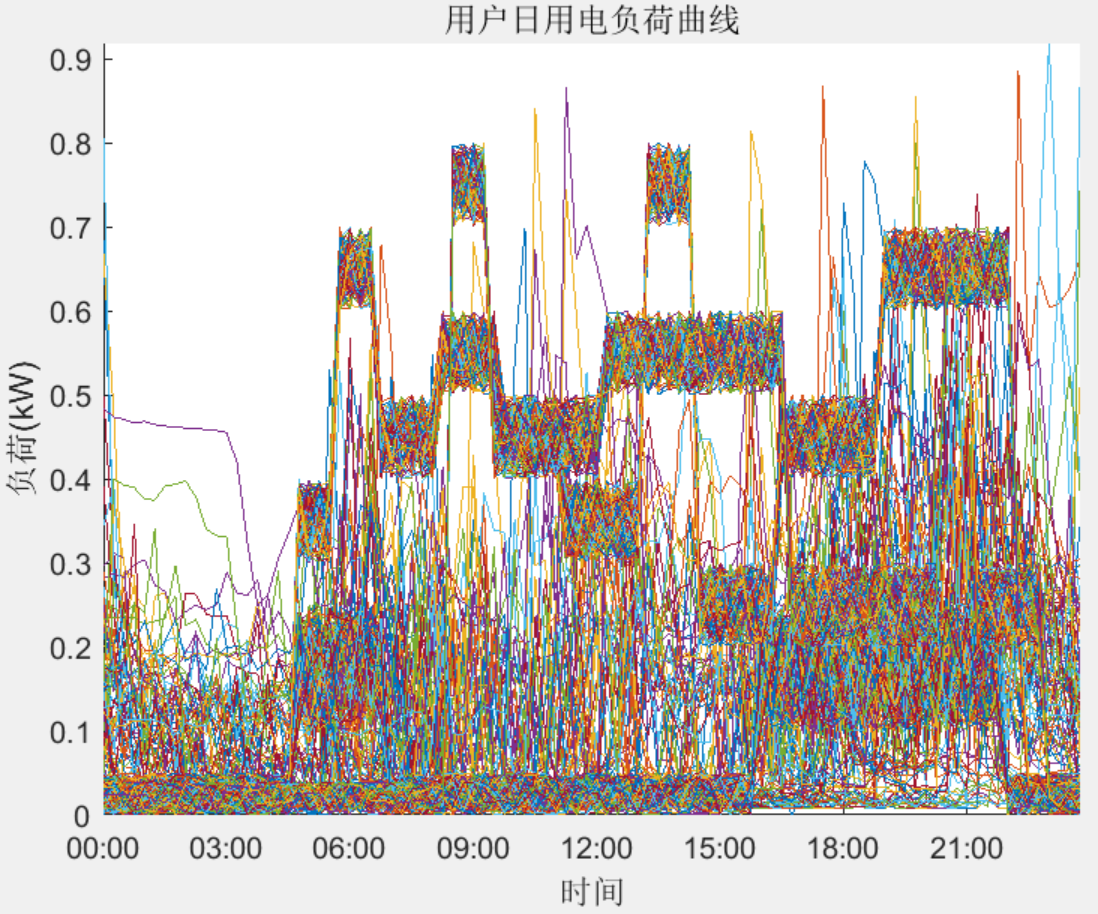
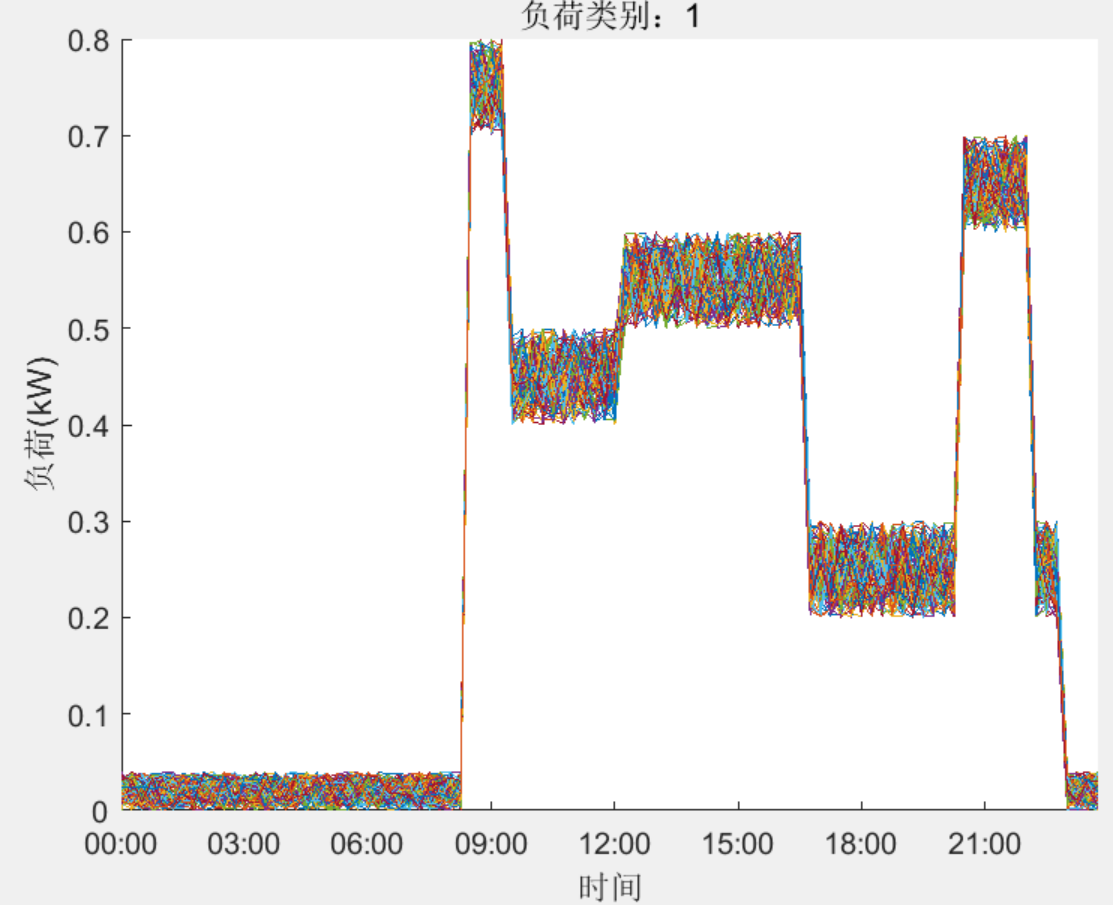
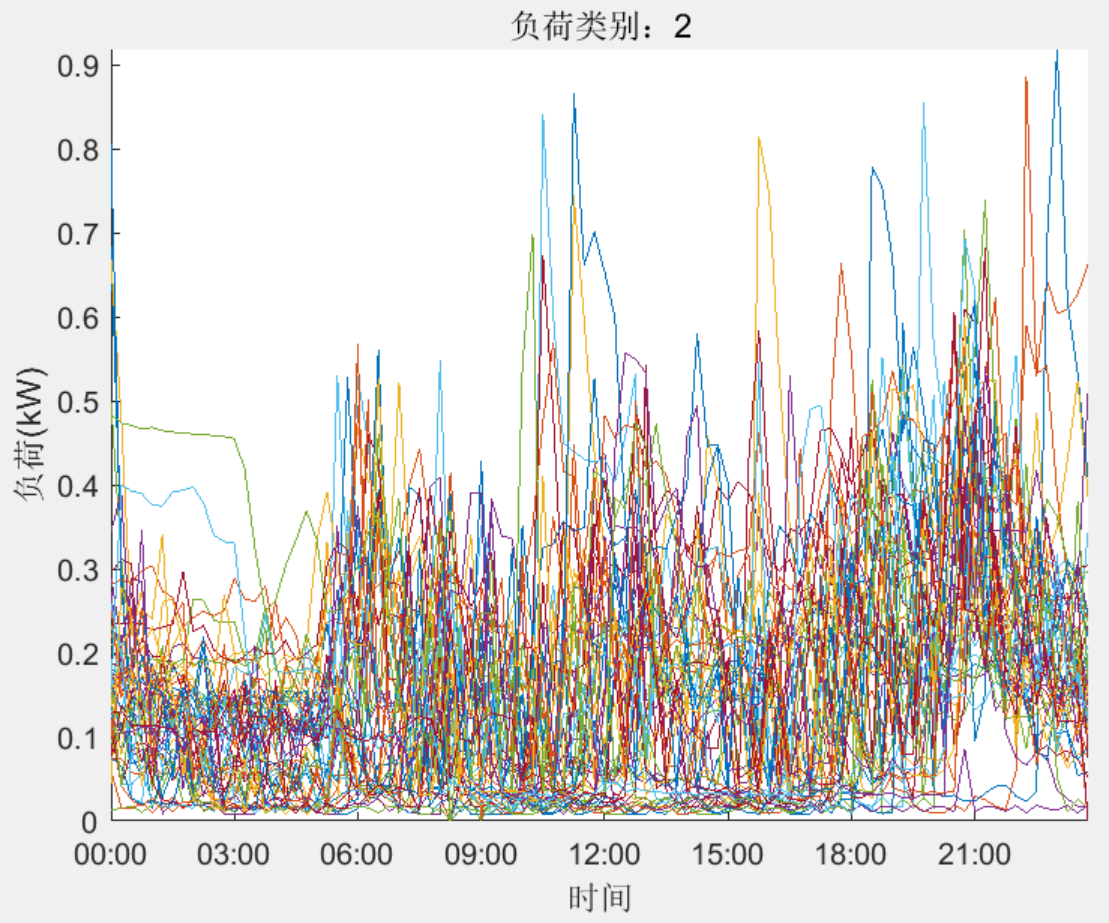
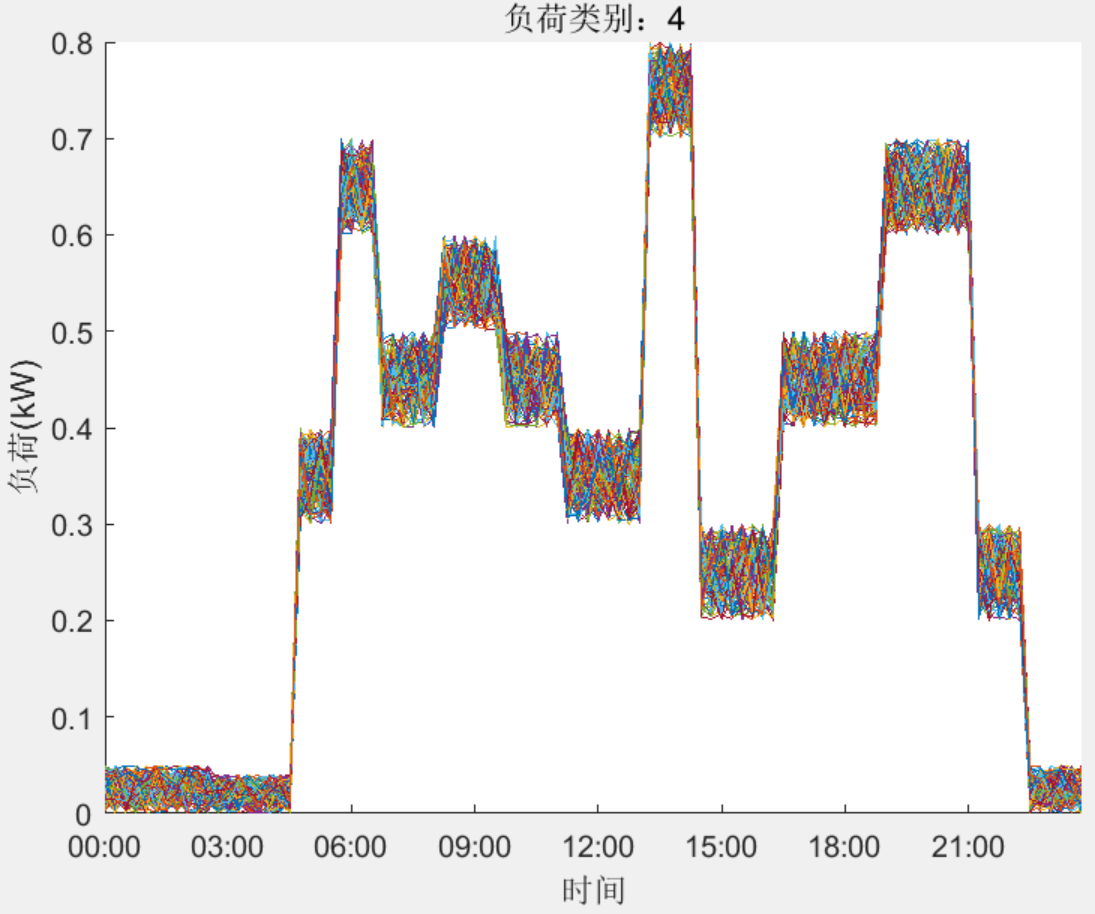
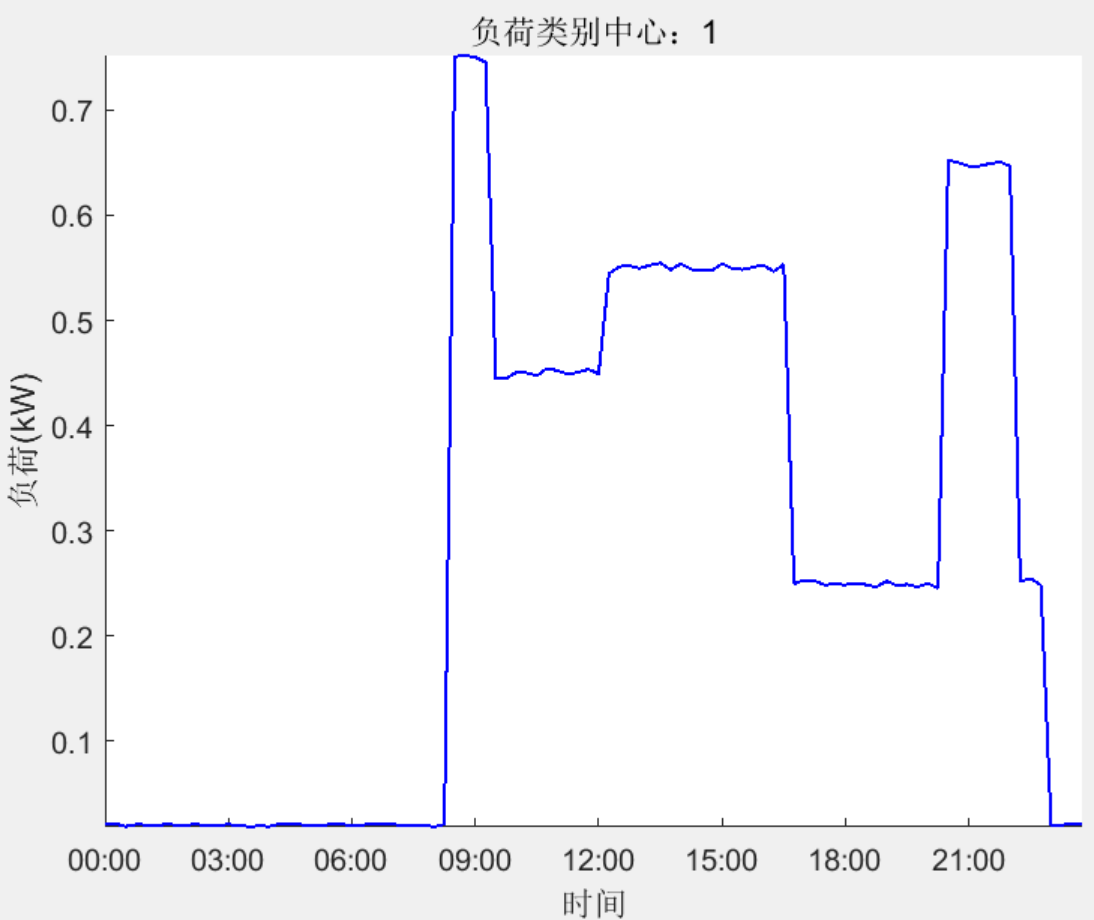
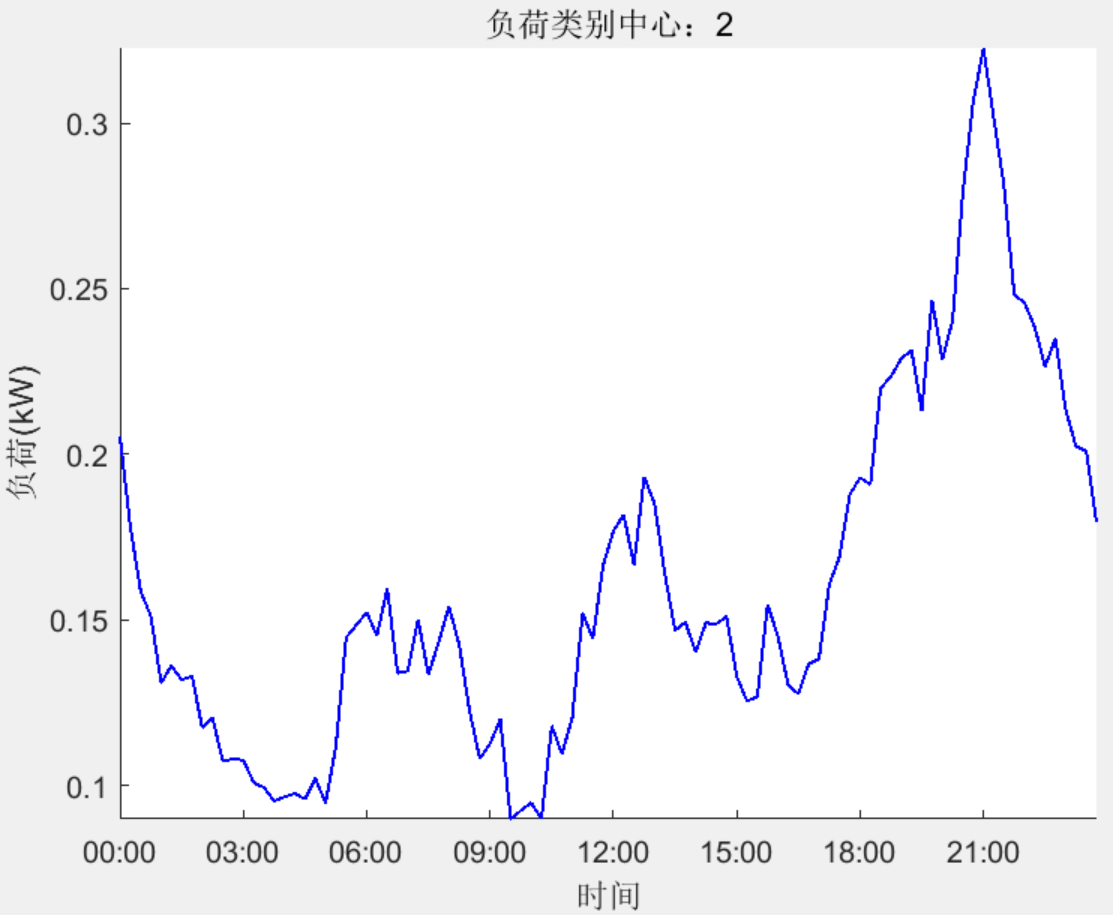
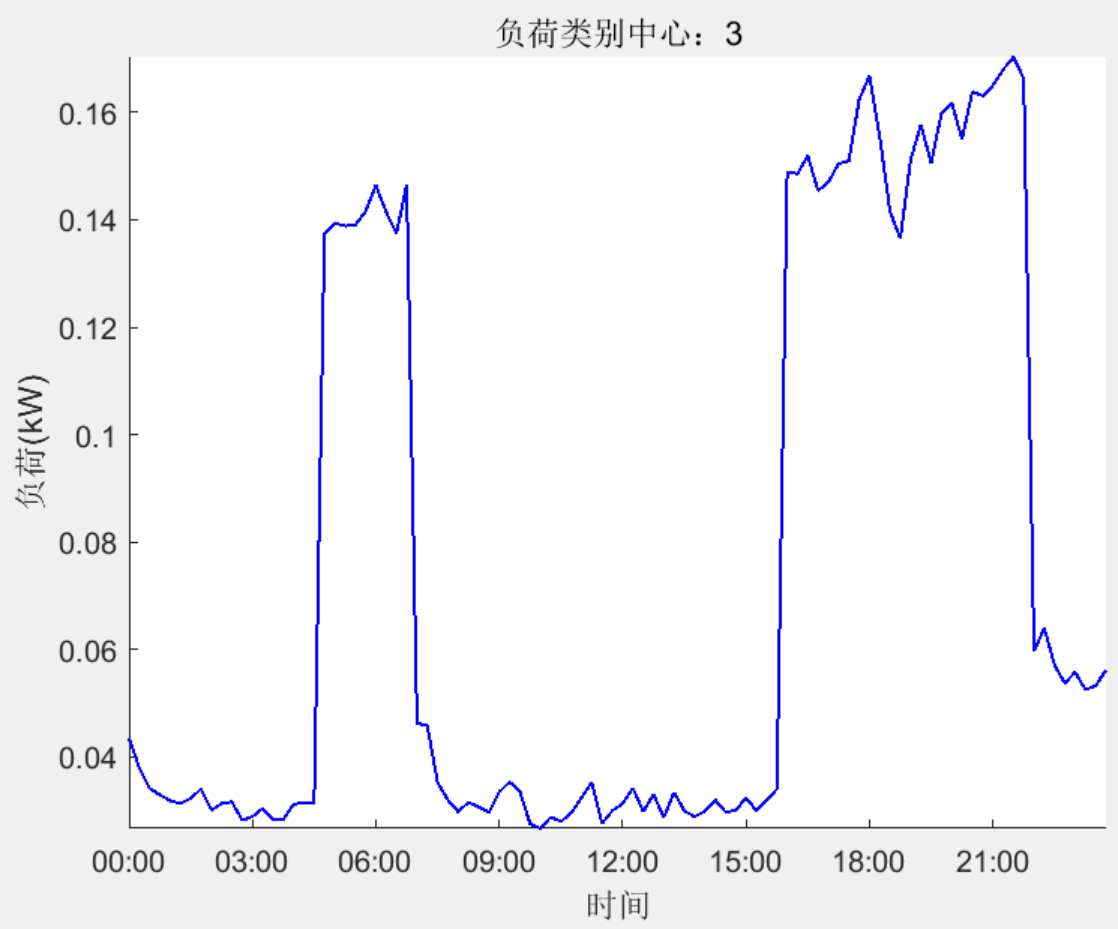
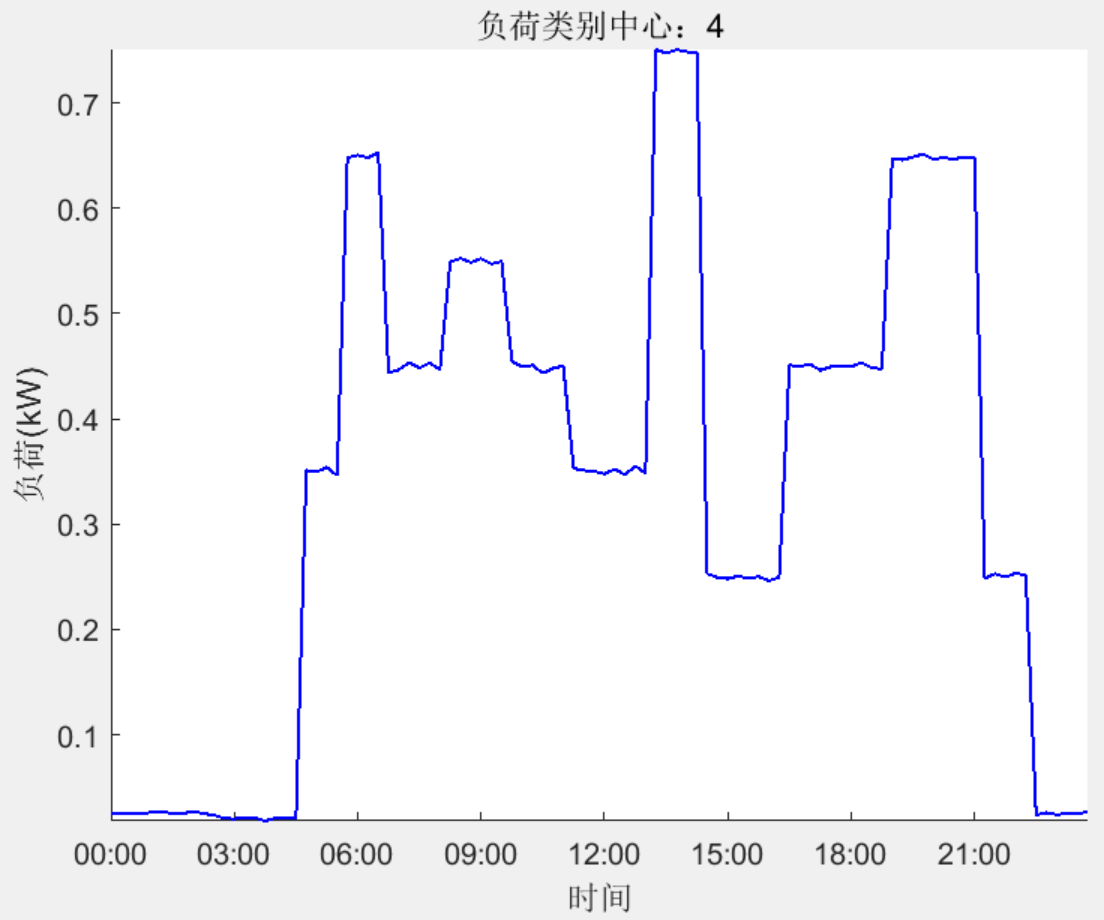
下载链接

原文地址：https://blog.csdn.net/superone89/article/details/139363609

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！