Scikit-Learn朴素贝叶斯
Scikit-Learn朴素贝叶斯
1、朴素贝叶斯
贝叶斯分类法是基于贝叶斯定理的统计学分类方法。它通过预测一组给定样本属于一个特定类的概率来进行分类。贝叶斯分类在机器学习知识结构中的位置如下:
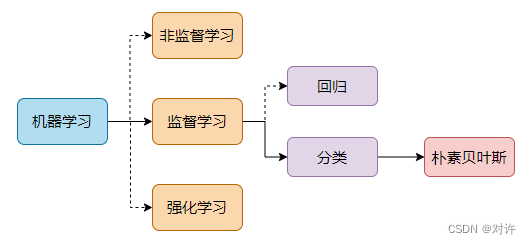
1.1、贝叶斯分类
贝叶斯分类的历史可以追溯到18世纪,当时英国统计学家托马斯·贝叶斯发展了贝叶斯定理,这个定理为统计决策提供了理论基础。不过,贝叶斯分类得到广泛实际应用是在20世纪80年代,当时计算机技术的进步使得大规模数据处理成为可能
在众多机器学习分类算法中,贝叶斯分类和其他绝大多数分类算法都不同
例如,KNN、逻辑回归、决策树等模型都是判别方法,也就是直接学习出输出Y和特征X之间的关系,即决策函数 Y Y Y= f ( X ) f(X) f(X)或决策函数 Y Y Y= P ( Y ∣ X ) P(Y|X) P(Y∣X)
但是,贝叶斯是生成方法,它直接找出输出Y和特征X的联合分布 P ( X , Y ) P(X,Y) P(X,Y),进而通过 P ( Y ∣ X ) P(Y|X) P(Y∣X)= P ( X , Y ) P ( X ) \frac{P(X,Y)}{P(X)} P(X)P(X,Y)计算得出结果判定
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素贝叶斯(Naive Bayes)分类是贝叶斯分类中最简单,也是常见的一种分类方法
朴素贝叶斯算法的核心思想是通过特征考察标签概率来预测分类,即对于给定的待分类样本,求解在此样本出现的条件下各个类别出现的概率,哪个最大,就认为此待分类样本属于哪个类别
例如,基于属性和概率原则挑选西瓜,根据经验,敲击声清脆说明西瓜还不够成熟,敲击声沉闷说明西瓜成熟度好,更甜更好吃。所以,坏瓜的敲击声是清脆的概率更大,好瓜的敲击声是沉闷的概率更大。当然这并不绝对——我们千挑万选的沉闷瓜也可能并没熟,这就是噪声了。当然,在实际生活中,除了敲击声,我们还有其他可能特征来帮助判断,例如色泽、根蒂、品类等
朴素贝叶斯把类似敲击声这样的特征概率化,构成一个西瓜的品质向量以及对应的好瓜/坏瓜标签,训练出一个标准的基于统计概率的好坏瓜模型,这些模型都是各个特征概率构成的。这样,在面对未知品质的西瓜时,我们迅速获取了特征,分别输入好瓜模型和坏瓜模型,得到两个概率值。如果坏瓜模型输出的概率值更大一些,那这个瓜很有可能就是个坏瓜
1.2、贝叶斯定理
贝叶斯定理(Bayes Theorem)也称贝叶斯公式,其中很重要的概念是先验概率、后验概率和条件概率
1.2.1、先验概率
先验概率是指事件发生前的预判概率。可以是基于历史数据的统计,可以由背景常识得出,也可以是人的主观观点给出。一般都是单独事件概率
例如,如果我们对西瓜的色泽、根蒂和纹理等特征一无所知,按照常理来说,好瓜的敲声是沉闷的概率更大,假设是60%,那么这个概率就被称为先验概率
1.2.2、后验概率
后验概率是指事件发生后的条件概率。后验概率是基于先验概率求得的反向条件概率。概率形式与条件概率相同
例如,我们了解到判断西瓜是否好瓜的一个指标是纹理。一般来说,纹理清晰的西瓜是好瓜的概率更大,假设是75%,如果把纹理清晰当作一种结果,然后去推测好瓜的概率,那么这个概率就被称为后验概率
1.2.3、条件概率
条件概率是指一个事件发生后另一个事件发生的概率。一般的形式为P(B|A),表示事件A已经发生的条件下,事件B发生的概率
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
1.2.4、贝叶斯公式
贝叶斯公式是基于假设的先验概率与给定假设下观察到不同样本数据的概率提供了一种计算后验概率的方法。朴素贝叶斯模型依托于贝叶斯公式
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
贝叶斯公式中:
- P(A)是事件A的先验概率,一般都是人主观给定的。贝叶斯中的先验概率一般特指它
- P(B)是事件B的先验概率,与类别标记无关,也称标准化常量,通常使用全概率公式计算得到
- P(B|A)是条件概率,又称似然概率,一般通过历史数据统计得到
- P(A|B)是后验概率,后验概率是我们求解的目标
由于P(B)与类别标记无关,因此估计P(A|B)的问题最后就被我们转化为基于训练数据集样本先验概率P(A)和条件概率P(B|A)的估计问题
贝叶斯公式揭示了事件A在事件B发生条件下的概率与事件B在事件A发生条件下的概率的关系
更多关于条件概率、全概率公式与贝叶斯公式的介绍详见文章:传送门
1.3、贝叶斯定理的推导
根据条件概率公式可得
P ( A B ) = P ( B ∣ A ) P ( A ) P(AB)=P(B|A)P(A) P(AB)=P(B∣A)P(A)
同理可得
P ( B A ) = P ( A ∣ B ) P ( B ) P(BA)=P(A|B)P(B) P(BA)=P(A∣B)P(B)
设事件A与事件B互相独立,即 P ( A B ) P(AB) P(AB)= P ( B A ) P(BA) P(BA),则有
P ( B ∣ A ) P ( A ) = P ( A ∣ B ) P ( B ) P(B|A)P(A)=P(A|B)P(B) P(B∣A)P(A)=P(A∣B)P(B)
由此可得贝叶斯公式
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
1.4、朴素贝叶斯及原理
基于贝叶斯定理的贝叶斯模型是一类简单常用的分类算法。在假设待分类项的各个属性相互独立的前提下,构造出来的分类算法就称为朴素的,即朴素贝叶斯算法
所谓朴素,就是假定所有输入事件之间相互独立。进行这个假设是因为独立事件间的概率计算更简单,当然,也更符合我们的实际生产生活
朴素贝叶斯模型的基本思想是,对于给定的待分类项 X { x 1 , x 2 , . . . , x n } X\{ {x_1,x_2,...,x_n}\} X{ x1,x2,...,xn},求解在此项出现的条件下各个类别 P ( y i ∣ X ) P(y_i|X)
原文地址:https://blog.csdn.net/weixin_55629186/article/details/139092457
免责声明:本站文章内容转载自网络资源,如侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
