稀疏最大谐波噪声比解卷积算法MATLAB实战
稀疏最大谐波噪声比解卷积(SMHD)算法是一种信号处理方法,特别是在处理含有噪声和谐波分量的复杂信号时表现出色。在信号处理领域,经常需要从被噪声和谐波干扰的信号中提取出有用的信息。传统的解卷积方法可能需要预先设定故障周期等参数,这在实际应用中往往难以实现。而SMHD算法则无需设定这些参数,能够自适应地从信号中估计出故障周期,并有效地抑制噪声和谐波分量,从而恢复出更清晰的信号。
一、算法原理
SMHD算法首先通过滤波信号的包络来计算谐波噪声比,算法不断迭代估计信号的谐波成分和噪声成分,并计算相应的谐波噪声比。基于谐波噪声比的计算结果,SMHD算法能够自适应地估计出信号的故障周期。在估计出故障周期后,SMHD算法会利用这一信息对信号进行解卷积处理来消除信号中的传递路径衰减和噪声干扰,从而恢复出原始的信号成分。
算法的优点:
1.无需设定故障周期:与传统的解卷积方法相比,SMHD算法无需预先设定故障周期等参数,能够自适应地从信号中估计出这些参数。
2.有效抑制噪声和谐波:通过计算谐波噪声比并自适应地估计故障周期,SMHD算法能够有效地抑制信号中的噪声和谐波分量。
3.提高信号恢复质量:由于能够准确地估计出故障周期并进行解卷积处理,SMHD算法能够恢复出更清晰、更准确的信号成分。
二、代码实战
SMHD算法不仅克服了传统解卷积方法如最小熵解卷积(MED)和最大相关峰态解卷积(MCKD)的局限性,而且在没有提前提供故障周期的情况下也能进行有效的故障特征检测。
通过模拟和不同测试台的轴承数据验证,SMHD算法在检测各种轴承故障方面表现出了有效性,与传统的MED和MCKD方法相比,SMHD在视觉检查和效率上都有更好的表现。具体代码如下所示:
clear
close all
clc
%%
load sig3
x = x - mean(x);
addpath('..\00 subfunction\')
%%
fs = 20000;
N = length(x);
t = (0:N - 1) / fs;
t = t(:);
BPFI = 38;
%% Raw data
figure;
plot(t, x, 'b');
xlabel('Time [s]')
ylabel('Amplitude')
title('Raw data')
legend(['Kurtosis=', num2str(kurtosis(x))])
setfontsize(20);
set(gcf, 'position', [100, 100, 800, 400])
axis tight
ylim([-2 2.5])
envelope_x = abs(hilbert(x)) - mean(abs(hilbert(x)));
ff = 0:fs / N:fs - fs / N;
amp_envelope_x = abs(fft(envelope_x, N)) * 2 / fs;
figure;
plot(ff, amp_envelope_x, 'b')
xlabel('Frequency [Hz]')
ylabel('Amplitude')
setfontsize(20);
set(gcf, 'position', [100, 100, 800, 400])
axis tight
xlim([0, 200]);
ylim([0 0.025])
%% SMHD
[y_final, f_final, kurtIter] = smhd(fs, x, 100, 30, 1.5 * rms(x), [], 0);
%% Filtered signal
figure;
plot(t, y_final, 'b');
xlabel('Time [s]')
ylabel('Amplitude')
title('Filtered signal by SMHD')
legend(['Kurtosis=', num2str(kurtosis(y_final))])
setfontsize(20);
set(gcf, 'position', [100, 100, 800, 400])
axis tight
ylim([-3.5 4.5])
envelope_y = abs(hilbert(y_final)) - mean(abs(hilbert(y_final)));
amp_envelope_y = abs(fft(envelope_y, N)) * 2 / fs;
figure;
plot(ff, amp_envelope_y, 'b')
xlabel('Frequency [Hz]')
ylabel('Amplitude')
setfontsize(20);
set(gcf, 'position', [100, 100, 800, 400])
axis tight
xlim([0, 200]);
ylim([0 0.3])
function [y_final, f_final, kurtIter] = smhd(fs, x, filterSize, termIter, mu, T, plotMode)
if isempty(filterSize)
filterSize = 100;
end
if isempty(termIter)
termIter = 30;
end
if isempty(mu)
mu = mean(x);
end
%% SMHD
x = x(:);
N = length(x);
L = filterSize;
%%%%%%%%% Initialize the fault signal period %%%%%%%%%
if isempty(T)
xxenvelope = abs(hilbert(x)) - mean(abs(hilbert(x)));
[T, ~] = TT(xxenvelope, fs);
end
T = round(T);
autoCorr = zeros(1, L);
for k = 0:L - 1
x2 = zeros(N, 1);
x2(k + 1:end) = x(1:end - k);
autoCorr(k + 1) = autoCorr(k + 1) + sum(x .* x2);
end
A = toeplitz(autoCorr);
A_inv = inv(2 .* A);
f = zeros(L, 1);
y1 = zeros(size(x));
kurtIter = [];
hnr = [];
deltah = [];
deltak = [];
% Initialize the filter coefficients
f(round(L / 2)) = 1;
f(round(L / 2) + 1) = -1;
n = 1;
%%%%%%%%% Iterate to solve the optimal filter coefficients %%%%%%%%%
while n == 1 || (n <= termIter)
y = filter(f, 1, x);
kurtIter(n) = kurtosis(y);
yenvelope = abs(hilbert(y)) - mean(abs(hilbert(y)));
[~, hnr(n)] = TT(yenvelope, fs);
y = y .* (1 - exp(-y.^2 / (2 * mu^2)));
weightedCrossCorr = zeros(L, 1);
for k = 0:L - 1
x2 = zeros(N, 1);
x3 = zeros(N, 1);
x2(k + 1:end - T) = x(T + 1:end - k);
x3(k + 1:end) = x(1:end - k);
y1(1:end - T) = y(T + 1:end);
weightedCrossCorr(k + 1) = weightedCrossCorr(k + 1) + ((sum(y .* x2) + sum(y1 .* x3)) .* sum(y.^2)) ./ sum(y .* y1);
end
f = A_inv * weightedCrossCorr;
f = f / sqrt(sum(f.^2));
n = n + 1;
%%%%%%%%% Update the sparse threshold %%%%%%%%%
[~, temp_hnr] = TT(y, fs);
deltah(n) = (temp_hnr - hnr(n - 1));
deltak(n) = (kurtosis(filter(f, 1, x)) / kurtIter(n - 1));
if deltak(n) > 1
deltak(n) = 1 + 0.02 * (deltak(n) + 1) / deltak(n);
else
deltak(n) = 1 - 0.02 * (deltak(n) + 1) / deltak(n);
end
mu = mu * deltak(n);
% update
xyenvelope = abs(hilbert(y)) - mean(abs(hilbert(y)));
[T, ~] = TT(xyenvelope, fs);
%%%%%%%%% Determine the maximum number of iterations %%%%%%%%%
if n == 2
hnrmax = hnr(1);
elseif hnr(n - 1) > hnrmax
hnrmax = hnr(n - 1);
y_final = y;
f_final = f;
end
end
disp(['The number of iteration is ', num2str(n - 1)])
%%%%%%%%% Display the processed signal %%%%%%%%%
if plotMode == 1
figure
plot((0:length(y_final) - 1) / fs, y_final, 'r')
title('Filtered signal by SHMD')
xlabel('Times[s]')
ylabel('Amplitude[g]')
set(gcf, 'position', [400, 400, 800, 400])
legend(['Kurtosis=', num2str(kurtosis(y_final))])
if n - 1 == termIter
disp('Terminated for iteration condition.')
else
disp('Terminated for minimum change in kurtosis condition.')
end
end
end
function [T, HNR] = TT (y, fs)
%find the maximum lag M
M = fs;
NA = xcorr(y, y, M, 'coeff');
NA = NA(ceil(length(NA) / 2):end);
% find first zero-crossing
sample1 = NA(1);
for lag = 2:length(NA)
sample2 = NA(lag);
if ((sample1 > 0) && (sample2 < 0))
zeroposi = lag;
break;
elseif ((sample1 == 0) || (sample2 == 0))
zeroposi = lag;
break;
else
sample1 = sample2;
end
end
% Cut from the first zero-crossing
NA = NA(zeroposi:end);
% Find the max position (time lag)
% corresponding the max aside from the first zero-crossing
[max_value, max_position] = max(NA);
% Give the extimated period by autocorrelation
T = zeroposi + max_position;
% Calculate the harmonic energy
HR = max_value;
% Calculate the harmonic-to-noise ratio
HNR = (HR / (1 - HR));
end进而可以得到SMHD算法的仿真结果,通过在每个迭代步骤中使用稀疏因子,SMHD算法进一步抑制噪声,提高滤波信号的信噪比。
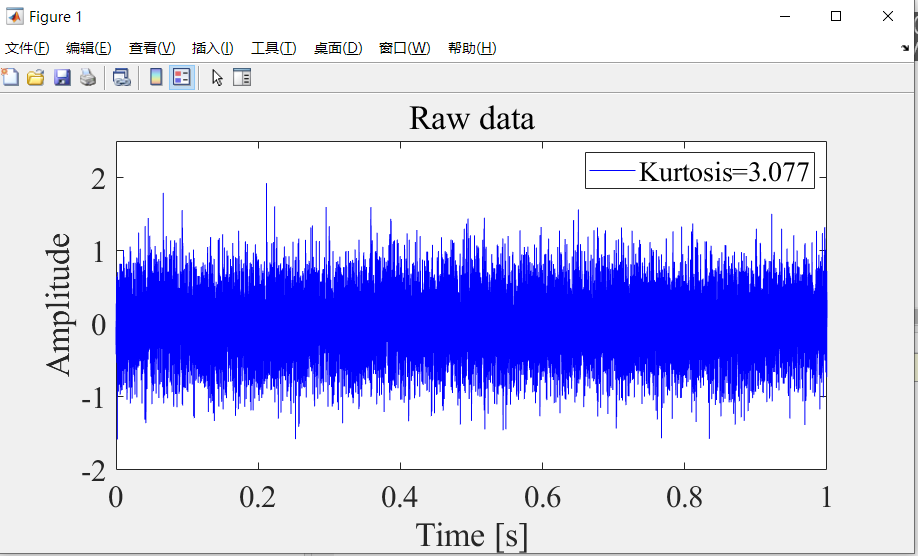
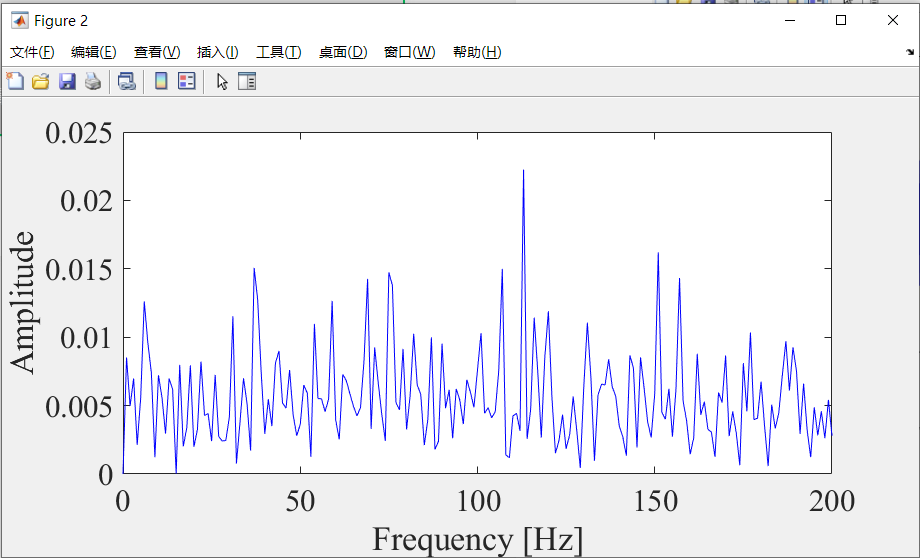
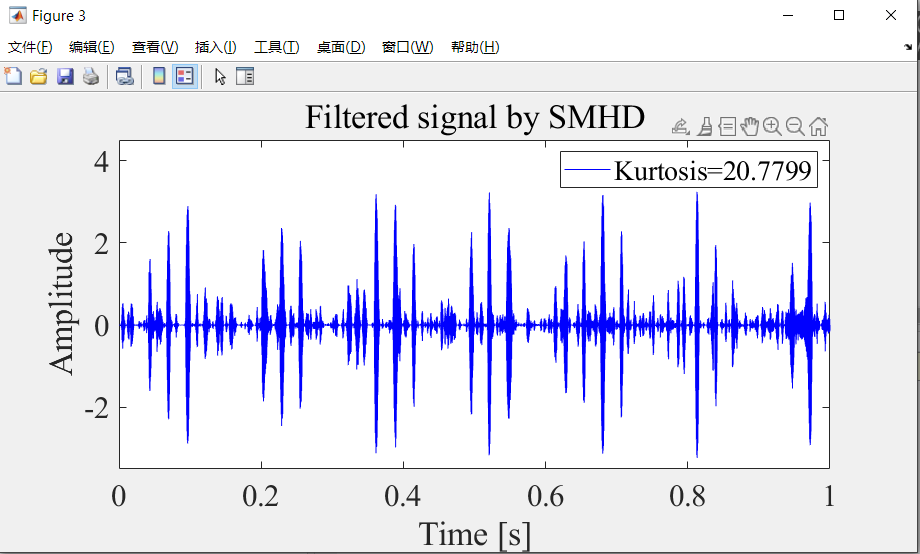
综上所述,稀疏最大谐波噪声比解卷积算法是一种强大的工具,它通过最大化HNR和利用信号的稀疏性,有效地从噪声中提取出微弱的故障特征,特别适用于故障诊断和信号处理领域。
原文地址:https://blog.csdn.net/2401_88845856/article/details/143957095
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
