DeepResBat: 深度残差批次和谐化方法考虑协变量分布差异|文献速递-生成式模型与transformer在医学影像中的应用

Title

题目

DeepResBat: Deep residual batch harmonization accounting for covariatedistribution differences

DeepResBat: 深度残差批次和谐化方法考虑协变量分布差异

01

文献速递介绍

随着对跨多个站点合并MRI数据的兴趣不断增长，诸如ENGIMA（Thompson et al., 2017）和ABCD（Volkow et al., 2018）等大型分析促进了神经影像学研究的发展，增强了统计功效（Bethlehem et al., 2022; Marek et al., 2022），提高了可推广性（He et al., 2022; Lu et al., 2022），并能够检测到细微的效应（Vogel et al., 2021; Tian et al., 2023）。在合并多个数据集时，后期获取和谐化是必需的，以去除不希望出现的站点间变异性，同时保留相关的生物学信息。跨数据集异质性的一个主要来源是扫描仪的差异（Magnotta et al., 2012; Chen et al., 2014; Hawco et al., 2018）。此外，生物学变量（例如人口统计学和临床诊断）的分布也可能在不同数据集间有所不同。这些生物学变量（也称为“协变量”）可能对MRI数据产生较大影响（Hua et al., 2010），其效应应在和谐化后保留下来。

一种流行的MRI数据和谐化方法是混合效应模型，如ComBat（Fortin et al., 2017, 2018; Yu et al., 2018）。ComBat通过包括协变量来去除加法和乘法的站点差异。例如，为了使用多个阿尔茨海默病（AD）痴呆数据集进行大数据分析，ComBat模型可能设置为海马体积为因变量，站点为自变量，同时将年龄、性别和临床诊断作为协变量。这样，海马体积中的加法和乘法站点效应被去除，而年龄、性别和临床诊断的残余效应被保留。为了增强和谐化表现，提出了多个ComBat变体（Garcia-Dias et al., 2020; Pomponio et al., 2020; Wachinger et al., 2021）。然而，ComBat变体的简洁性（和优雅性）限制了它们去除跨脑区非线性站点差异的能力。

深度神经网络（DNN）在去除分布于大脑各区域的非线性站点差异方面表现出色（Dewey et al., 2019; Hu et al., 2023）。基于变分自编码器（VAE）的方法（Moyer et al., 2020; Russkikh et al., 2020; Zuo et al., 2021; An et al., 2022; Hu et al., 2024）使用编码器从输入的MRI数据生成站点不变的潜在表示，然后将站点信息与潜在表示连接，通过解码器重建MRI数据。生成对抗网络（Zhao et al., 2019; Modanwal et al., 2020; Bashyam et al., 2021）、归一化流（Wang et al., 2021; Beizaee et al., 2023）和联邦学习（Dinsdale et al., 2022）也已被探索。然而，现有的DNN方法通常忽视了协变量的包含，而混合效应和谐化模型（Fortin et al., 2017, 2018; Chen et al., 2022）则明确控制了协变量。由于协变量分布差异在不同数据集之间是不可避免的，如果在和谐化过程中忽略了协变量，可能会无意中去除相关的生物学信息，而不是减少不希望出现的数据集差异，从而导致下游表现变差。我们在2.1节中展示了如何利用一个理论的机器学习结果（Tachet et al., 2020）来理解这一现象。

在本研究中，我们提出了两种基于深度学习的协变量感知和谐化技术：协变量VAE（coVAE）和深度残差批次效应和谐化（DeepResBat）。coVAE通过将协变量和站点信息与站点和协变量不变的潜在表示连接，扩展了条件VAE（cVAE; Moyer et al., 2020）。另一方面，DeepResBat采用了一个受经典ComBat方法启发的残差框架。DeepResBat首先使用非线性回归树去除协变量效应，然后通过cVAE从残差中消除不必要的站点差异。最后，将协变量效应重新添加到和谐化后的残差中。我们发现，coVAE即使在没有关联的情况下，也会产生解剖MRI与协变量之间的虚假关联，表明基于DNN的和谐化方法可能在和谐化过程中引入假阳性。另一方面，DeepResBat有效地缓解了这一假阳性问题。

本研究的贡献有多方面。首先，我们理论上表明，忽视不同数据集之间的协变量差异会导致和谐化效果不理想。其次，我们提出了一种基于DNN的和谐化方法DeepResBat，能够考虑不同数据集之间的协变量差异。DeepResBat在多个评估实验中表现优于ComBat（Fortin et al., 2017）、CovBat（Chen et al., 2021）和cVAE（Moyer et al., 2020），不仅增强了生物学效应，同时去除了不希望的数据集差异。第三，我们展示了基于DNN的和谐化方法可能会在协变量和MRI测量之间产生关系，即使没有实际存在的关联。因此，未来提出基于DNN的和谐化方法的研究应警惕这一假阳性陷阱。尽管当前研究集中在MRI数据上，但我们的结果适用于任何需要仪器和谐化的领域，例如分子生物学（Johnson et al., 2007）、地质学（Madonna et al., 2022）或农业（Leroux et al., 2019）。

Aastract

摘要

Pooling MRI data from multiple datasets requires harmonization to reduce undesired inter-site variabilities,while preserving effects of biological variables (or covariates). The popular harmonization approach ComBatuses a mixed effect regression framework that explicitly accounts for covariate distribution differences acrossdatasets. There is also significant interest in developing harmonization approaches based on deep neural networks (DNNs), such as conditional variational autoencoder (cVAE). However, current DNN approaches do notexplicitly account for covariate distribution differences across datasets. Here, we provide mathematical results,suggesting that not accounting for covariates can lead to suboptimal harmonization. We propose two DNN-basedcovariate-aware harmonization approaches: covariate VAE (coVAE) and DeepResBat. The coVAE approach is anatural extension of cVAE by concatenating covariates and site information with site- and covariate-invariantlatent representations. DeepResBat adopts a residual framework inspired by ComBat. DeepResBat firstremoves the effects of covariates with nonlinear regression trees, followed by eliminating site differences withcVAE. Finally, covariate effects are added back to the harmonized residuals. Using three datasets from threecontinents with a total of 2787 participants and 10,085 anatomical T1 scans, we find that DeepResBat and coVAEoutperformed ComBat, CovBat and cVAE in terms of removing dataset differences, while enhancing biologicaleffects of interest. However, coVAE hallucinates spurious associations between anatomical MRI and covariateseven when no association exists. Future studies proposing DNN-based harmonization approaches should beaware of this false positive pitfall. Overall, our results suggest that DeepResBat is an effective deep learningalternative to ComBat.

将来自多个数据集的MRI数据进行合并时，需要进行和谐化以减少不希望出现的站点间变异性，同时保持生物学变量（或协变量）的效应。流行的和谐化方法ComBat采用了混合效应回归框架，明确考虑了不同数据集之间协变量分布的差异。与此同时，基于深度神经网络（DNN）的和谐化方法，如条件变分自编码器（cVAE），也引起了广泛关注。然而，当前的DNN方法并未明确考虑不同数据集之间的协变量分布差异。在本研究中，我们提供了数学结果，表明如果不考虑协变量，会导致和谐化效果不理想。我们提出了两种基于DNN的协变量感知和谐化方法：协变量VAE（coVAE）和DeepResBat。coVAE方法通过将协变量和站点信息与站点和协变量不变的潜在表示连接起来，作为cVAE的自然扩展。DeepResBat采用了一个受ComBat启发的残差框架。DeepResBat首先使用非线性回归树去除协变量的效应，然后利用cVAE消除站点差异。最后，将协变量效应重新添加到和谐化后的残差中。使用来自三大洲的三个数据集，总计2787名参与者和10,085个解剖T1扫描，我们发现DeepResBat和coVAE在去除数据集差异方面优于ComBat、CovBat和cVAE，同时增强了生物学效应。然而，即使在没有关联的情况下，coVAE也会产生虚假的解剖MRI与协变量之间的关联。未来提出基于DNN的和谐化方法的研究应警惕这一假阳性陷阱。总体而言，我们的研究结果表明，DeepResBat是一个有效的深度学习替代方案，能够替代ComBat。

Method

方法

2.1. Motivation for accounting for covariates during harmonizationDistribution differences in covariates, such as demographics andclinical diagnoses, across datasets are inevitable. Most deep learningharmonization approaches directly align distributions of latent representations across datasets without explicitly modeling covariate differences (Dewey et al., 2019; Zuo et al., 2021; Beizaee et al., 2023; Liuet al., 2023). Without explicitly accounting for these covariates, thecovariates differences can be misinterpreted as undesirable dataset differences and wrongly removed by the harmonization algorithms. Here,we will formalize this phenomenon using a theoretical result from themachine learning literature (Tachet et al., 2020).

2.1. 说明在和谐化过程中考虑协变量的动机

跨数据集的协变量（如人口统计学和临床诊断）分布差异是不可避免的。大多数深度学习和谐化方法直接对齐跨数据集的潜在表示分布，而没有明确建模协变量差异（Dewey et al., 2019; Zuo et al., 2021; Beizaee et al., 2023; Liu et al., 2023）。如果没有明确考虑这些协变量，协变量的差异可能会被误解为不希望出现的数据集差异，并且被和谐化算法错误地去除。在这里，我们将使用机器学习文献中的理论结果（Tachet et al., 2020）来形式化这一现象。

Conclusion

结论

In this study, we demonstrate the importance of incorporatingcovariates during harmonization. We propose two deep learning models,coVAE and DeepResBat, that account for covariate distribution differences across datasets. coVAE extends cVAE by concatenating covariatesand site information with latent representations, while DeepResBatadopts a residual framework inspired by the classical ComBat framework. We found that coVAE introduces spurious associations betweenanatomical MRI and unrelated covariates, while DeepResBat effectivelymitigates this false positive issue. Furthermore, DeepResBat outperformed ComBat, CovBat and cVAE in terms of removing datasetdifferences, while retaining biological effects of interest.

在本研究中，我们展示了在协调过程中纳入协变量的重要性。我们提出了两种深度学习模型，coVAE 和 DeepResBat，能够考虑跨数据集的协变量分布差异。coVAE 通过将协变量和站点信息与潜在表示拼接在一起，从而扩展了 cVAE，而 DeepResBat 采用了一个残差框架，灵感来源于经典的 ComBat 框架。我们发现，coVAE 引入了解剖学 MRI 和无关协变量之间的虚假关联，而 DeepResBat 有效地缓解了这一假阳性问题。此外，DeepResBat 在去除数据集差异方面优于 ComBat、CovBat 和 cVAE，同时保留了感兴趣的生物学效应。

Results

结果

3.1. DNN models removed more dataset differences than classical mixedeffect modelsDataset prediction accuracies of matched participants are shown inFig. 4. Lower prediction accuracies indicated that greater dataset differences were removed, suggesting better harmonization quality.Fig. 4A shows the dataset prediction performance for matched ADNIand AIBL participants. Without harmonization, an XGBoost classifierachieved 100 % accuracy in identifying which dataset a participant’sdata came from. After applying mixed effect harmonization approaches(ComBat and CovBat), the prediction accuracy significantly dropped to0.695 ± 0.376 (mean ± std) for ComBat, and 0.670 ± 0.383 for CovBat,indicating a substantial reduction in dataset differences. Deep learningapproaches showed improved dataset difference removal, with performance of 0.595 ± 0.381 for cVAE and 0.592 ± 0.368 for coVAE. Ourproposed DeepResBat achieved an accuracy of 0.594 ± 0.375, whichwas not statistically different from the deep learning baselines (Table 2).Notably, all deep learning approaches exhibited significantly lowerdataset prediction accuracies than mixed effect approaches, demonstrating the potential of deep learning for data harmonization. However,the dataset prediction accuracies of all deep learning approachesremained better than chance (p = 1e-4), indicating residual datasetdifferences.

3.1. DNN 模型比经典混合效应模型去除更多数据集差异匹配参与者的数据集预测准确率如图 4 所示。较低的预测准确率表明去除了更多的数据集差异，这意味着更好的和谐化效果。图 4A 显示了匹配的 ADNI 和 AIBL 参与者的数据集预测表现。未经和谐化时，XGBoost 分类器能 100% 准确地识别参与者数据来源于哪个数据集。在应用混合效应和谐化方法（ComBat 和 CovBat）后，预测准确率显著下降，ComBat 为 0.695 ± 0.376（均值 ± 标准差），CovBat 为 0.670 ± 0.383，表明数据集差异显著减少。深度学习方法则显示出更好的数据集差异去除效果，其中 cVAE 的表现为 0.595 ± 0.381，coVAE 为 0.592 ± 0.368。我们提出的 DeepResBat 达到了 0.594 ± 0.375 的准确率，且与深度学习基准方法在统计学上没有显著差异（表 2）。值得注意的是，所有深度学习方法的预测准确率显著低于混合效应方法，显示了深度学习在数据和谐化中的潜力。然而，所有深度学习方法的数据集预测准确率仍然显著高于随机猜测（p = 1e-4），表明仍存在残留的数据集差异。

Figure

图

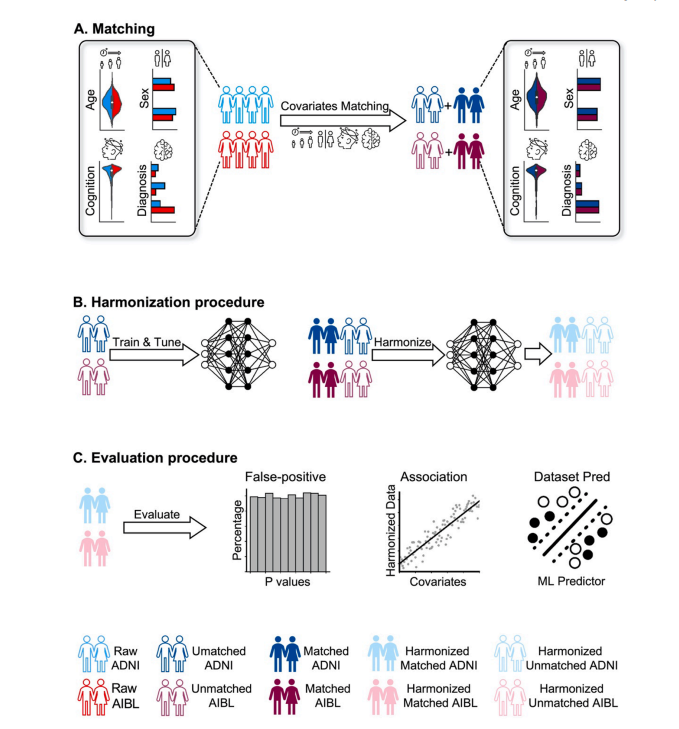
Fig. 1. Workflow of study. We illustrate the workflow using ADNI and AIBL. The same procedure was applied to ADNI and MACC. (A) ADNI and AIBL participantswere matched based on age, sex, mini mental-state examination (MMSE) and clinical diagnosis. The unmatched participants were used for training and tuningharmonization and evaluation models. The matched participants served as the test set for harmonization evaluation. (B) Left: Train harmonization models withunmatched participants. Right: Apply trained harmonization models on both unmatched and matched participants. (C) Three sets of evaluation experiments weretested on matched harmonized participants: dataset prediction experiment, association analysis and false positive experiment. In evaluations where training wasnecessary (dataset prediction and false positive experiments), unmatched participants were used as the training and validation sets for the evaluation experiments,while the matched participants were used as the test set.

图 1. 研究工作流程我们使用 ADNI 和 AIBL 数据集来说明工作流程。相同的程序也应用于 ADNI 和 MACC 数据集。(A) ADNI 和 AIBL 参与者根据年龄、性别、简易精神状态检查（MMSE）和临床诊断进行匹配。未匹配的参与者用于训练和调优和谐化及评估模型。匹配的参与者作为和谐化评估的测试集。(B) 左侧：使用未匹配的参与者训练和谐化模型。右侧：将训练好的和谐化模型应用于未匹配和匹配的参与者。(C) 对匹配和谐化参与者进行了三组评估实验：数据集预测实验、关联分析和假阳性实验。在需要训练的评估中（数据集预测和假阳性实验），未匹配的参与者作为训练集和验证集，而匹配的参与者作为测试集。

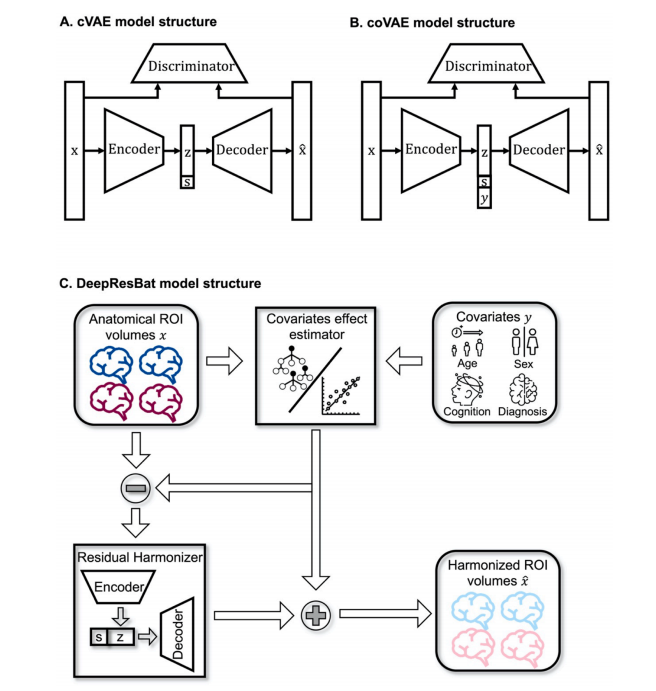
Fig. 2. Model structure for cVAE, coVAE, and DeepResBat. (A) Model structure for the cVAE model. Encoder, decoder, and discriminator were all fully connectedfeedforward DNNs. s was the site we wanted to map the brain volumes to. (B) Model structure for the coVAE model. Site s and covariates y were input into thedecoder to preserve covariates effects. Therefore, the main difference between cVAE and coVAE is the inclusion of covariates y. (C) Model structure for theDeepResBat model. The covariates effect estimator was an ensemble of XGBoost and linear models. Once the effects of covariates were removed (subtraction sign),the residual harmonizer was a cVAE model taking covariates-free residuals as input. The covariates effects were then added back to the cVAE output, yielding a finalset of harmonized ROI volumes.

图 2. cVAE、coVAE 和 DeepResBat 的模型结构(A) cVAE 模型的结构。编码器、解码器和判别器都是全连接的前馈深度神经网络（DNN）。s 是我们想要映射脑体积的站点。(B) coVAE 模型的结构。站点 s 和协变量 y 被输入到解码器中，以保留协变量的影响。因此，cVAE 和 coVAE 之间的主要区别在于协变量 y 的包含。(C) DeepResBat 模型的结构。协变量效应估计器是 XGBoost 和线性模型的集成。一旦去除协变量的影响（减号），剩余的和谐化器是一个 cVAE 模型，它以去除协变量影响后的残差作为输入。然后，协变量的效应被重新添加到 cVAE 输出中，得到最终的和谐化 ROI 体积集。

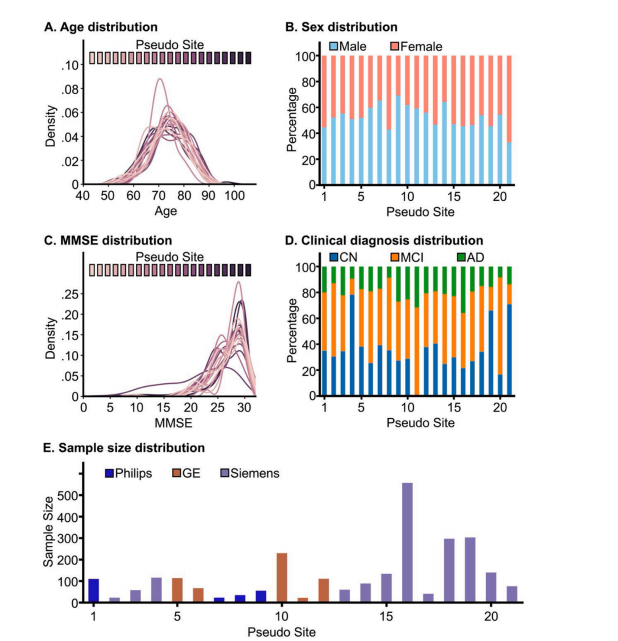
Fig. 3. Sample characteristics of 21 pseudo sites. (A) Age distribution for each pseudo site; (B) Sex distribution for each pseudo site; (C) MMSE distribution foreach pseudo site; (D) Clinical diagnosis distribution for each pseudo site; (D) Sample size distribution for each pseudo site, colored by MRI vendors

图 3. 21 个伪站点的样本特征(A) 每个伪站点的年龄分布；(B) 每个伪站点的性别分布；(C) 每个伪站点的 MMSE（简易精神状态检查）分布；(D) 每个伪站点的临床诊断分布；(E) 每个伪站点的样本大小分布，按 MRI 供应商着色。

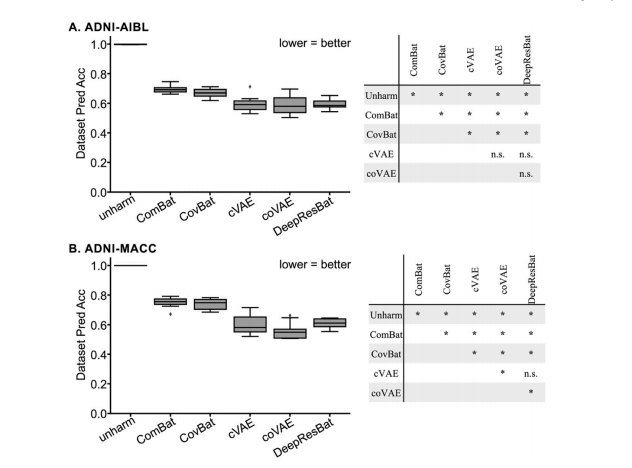
Fig. 4. Dataset prediction accuracies. (A) Left: Dataset prediction accuracies for matched ADNI and AIBL participants across 10 folds. Right: p values of differencesbetween different approaches. "" indicates statistical significance after surviving FDR correction (q < 0.05). "n.s." indicates not significant. (B) Same as (A) but formatched ADNI and MACC participants. All p values are reported in Tables 2 and 3.

图 4. 数据集预测准确率(A) 左图：匹配的 ADNI 和 AIBL 参与者在 10 个折中的数据集预测准确率。右图：不同方法之间差异的 p 值。"" 表示在 FDR 校正后具有统计学意义（q* < 0.05）。"n.s." 表示无显著差异。(B) 与 (A) 相同，但为匹配的 ADNI 和 MACC 参与者的数据。所有 p 值详见表 2 和表 3。

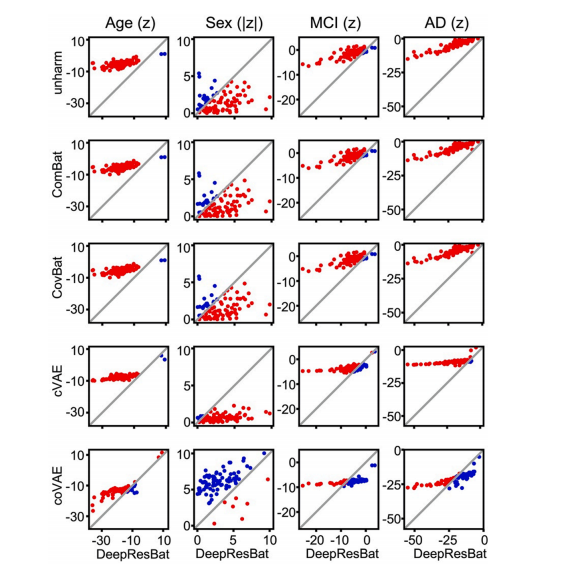
Fig. 5. Comparison of z statistics from GLM involving clinical diagnosis for DeepResBat and baselines on matched ADNI and AIBL participants. Each rowcompares DeepResBat and one baseline approach: no harmonization (row 1), ComBat (row 2), CovBat (row 3), cVAE (row 4) and coVAE (row 5). Each columnrepresents one covariate: age (column 1), sex (column 2), MCI (column 3) and AD dementia (column 4). Each subplot compares z statistics of DeepResBat againstanother baseline for a given covariate across 87 grey matter ROIs. Each dot represents one grey matter ROI. Red dots indicate better performance by DeepResBat.Blue dots indicate worse performance by DeepResBat

图 5. 基于临床诊断的 GLM z 统计量比较：DeepResBat 与基线方法在匹配的 ADNI 和 AIBL 参与者中的比较。每一行比较 DeepResBat 与一种基线方法：未进行 harmonization（第 1 行）、ComBat（第 2 行）、CovBat（第 3 行）、cVAE（第 4 行）和 coVAE（第 5 行）。每一列代表一个协变量：年龄（第 1 列）、性别（第 2 列）、MCI（第 3 列）和 AD 痴呆（第 4 列）。每个子图比较 DeepResBat 和另一基线方法在给定协变量下，87 个灰质 ROI 的 z 统计量。每个点代表一个灰质 ROI。红点表示 DeepResBat 的表现更好，蓝点表示 DeepResBat 的表现更差。

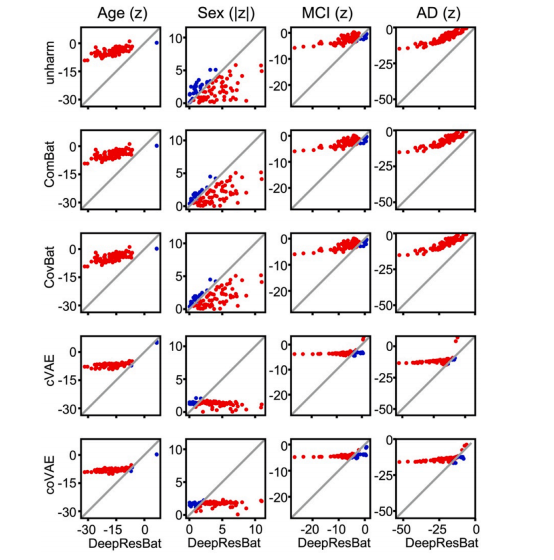
Fig. 6. Comparison of z statistics from GLM involving clinical diagnosis for DeepResBat and baselines on matched ADNI and MACC participants. Each rowcompares DeepResBat and one baseline approach: no harmonization (row 1), ComBat (row 2), CovBat (row 3), cVAE (row 4) and coVAE (row 5). Each columnrepresents one covariate: age (column 1), sex (column 2), MCI (column 3) and AD dementia (column 4). Each subplot compares z statistics of DeepResBat againstanother baseline for a given covariate across 87 grey matter ROIs. Each dot represents one grey matter ROI. Red dots indicate better performance by DeepResBat.Blue dots indicate worse performance by DeepResBat

图 6. 深度残差批次效应（DeepResBat）与基线方法在匹配的 ADNI 和 MACC 参与者中涉及临床诊断的 GLM 比较的 z 统计量。每一行比较 DeepResBat 和一个基线方法：未进行 harmonization（行 1），ComBat（行 2），CovBat（行 3），cVAE（行 4）和 coVAE（行 5）。每一列表示一个协变量：年龄（列 1），性别（列 2），轻度认知障碍（MCI，列 3）和阿尔茨海默病（AD）痴呆（列 4）。每个子图比较 DeepResBat 与基线方法在给定协变量下对 87 个灰质感兴趣区（ROI）的 z 统计量。每个点代表一个灰质 ROI。红点表示 DeepResBat 表现更好，蓝点表示 DeepResBat 表现较差。

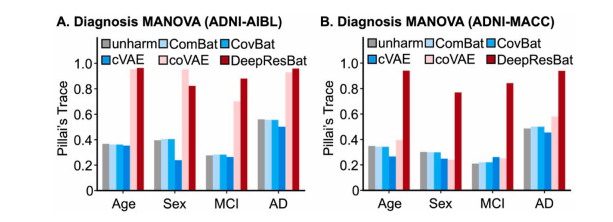
Fig. 7. Effect size of MANOVA involving clinical diagnosis. A larger Pillai’s Trace indicates a stronger association, and thus better performance. (A) Bar plot formatched ADNI and AIBL participants. (B) Bar plot for matched ADNI and MACC participants.

图 7. 涉及临床诊断的 MANOVA 效应量。较大的 Pillai’s Trace 表示更强的关联，因此表现更好。(A) 匹配的 ADNI 和 AIBL 参与者的条形图。(B) 匹配的 ADNI 和 MACC 参与者的条形图。

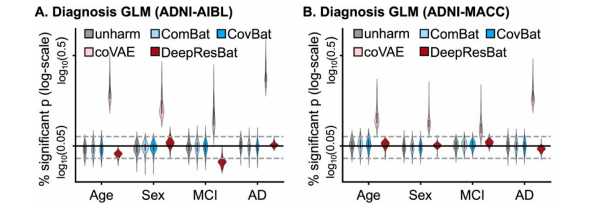
Fig. 8. Percentage of significant p values (i.e., p < 0.05) from GLM with clinical diagnosis after 1000 permutations of covariates. More specifically, eachdata point in the violin plot represents a brain ROI volume. Percentage is calculated based on the number of permutations in which p value of corresponding covariatewas significant (i.e., p < 0.05) divided by 1000 permutations. Percentage (vertical axis) is shown on a log scale. The black solid line is the expected percentage (whichis 0.05), while the grey dashed lines indicated 95 % confidence intervals. (A) GLM analysis involving clinical diagnosis for matched ADNI and AIBL participants. (B)GLM analysis involving clinical diagnosis for matched ADNI and MACC participants.

图 8. 经过 1000 次协变量置换后，涉及临床诊断的 GLM 显著性 p 值百分比 (即 p < 0.05)。更具体地说，小提琴图中的每个数据点代表一个大脑 ROI 体积。百分比是根据每次置换中相应协变量的 p 值显著性 (即 p < 0.05) 的次数与 1000 次置换的比例计算的。百分比（纵轴）以对数尺度显示。黑色实线表示预期百分比 (0.05)，灰色虚线表示 95% 置信区间。(A) 涉及临床诊断的 GLM 分析，适用于匹配的 ADNI 和 AIBL 参与者。(B) 涉及临床诊断的 GLM 分析，适用于匹配的 ADNI 和 MACC 参与者。

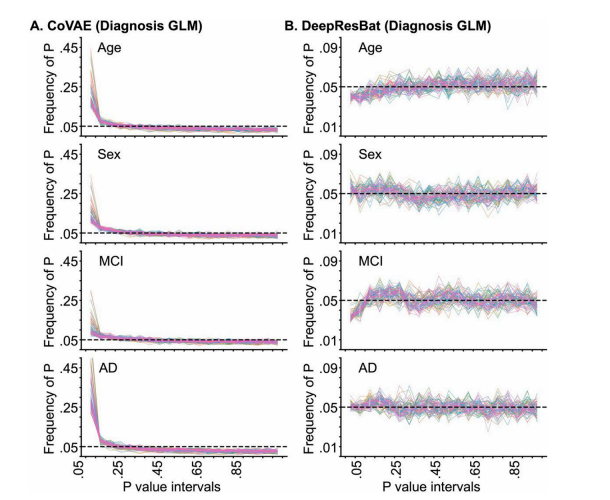
Fig. 9. Frequency of p values of coVAE and DeepResBat for matched ADNI and AIBL participants by GLM involving clinical diagnosis based on 1000permutations. Each line corresponds to a single brain ROI. P values were binned in intervals of 0.05. Therefore, in the ideal scenario, the distributions of p valuesshould follow a uniform distribution with a height of 0.05. (A) Frequency of p values for coVAE. (B) Frequency of p values for DeepResBat.

图 9. 基于 1000 次置换的 GLM 临床诊断分析，coVAE 和 DeepResBat 对匹配的 ADNI 和 AIBL 参与者的 p 值频率。每条线代表一个大脑 ROI。p 值按 0.05 的间隔分箱。因此，在理想情况下，p 值的分布应该呈现均匀分布，高度为 0.05。(A) coVAE 的 p 值频率。(B) DeepResBat 的 p 值频率。

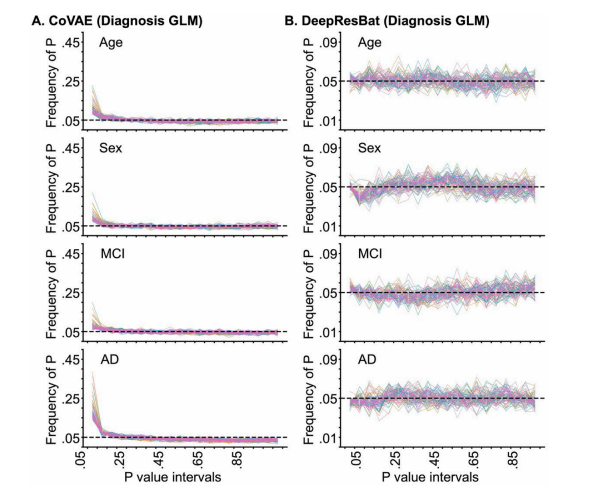
Fig. 10. Frequency of p values of coVAE and DeepResBat for matched ADNI and MACC participants by GLM involving clinical diagnosis based on 1000permutations. Each line corresponds to a single brain ROI. P values were binned in intervals of 0.05. Therefore, in the ideal scenario, the distributions of p valuesshould follow a uniform distribution with a height of 0.05. (A) Frequency of p values for coVAE. (B) Frequency of p values for DeepResBat.

图 10. 基于 1000 次置换的 GLM 临床诊断分析，coVAE 和 DeepResBat 对匹配的 ADNI 和 MACC 参与者的 p 值频率。每条线代表一个大脑 ROI。p 值按 0.05 的间隔分箱。因此，在理想情况下，p 值的分布应该呈现均匀分布，高度为 0.05。(A) coVAE 的 p 值频率。(B) DeepResBat 的 p 值频率。

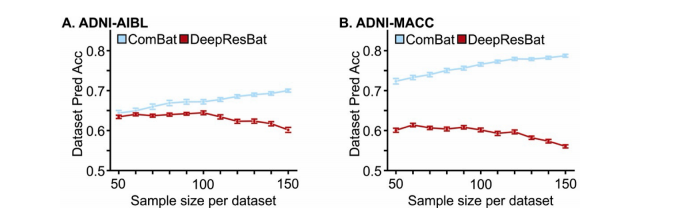
Fig. 11. Dataset prediction accuracies for ComBat and DeepResBat with different sample sizes per dataset. Each sampling was repeated 50 times. Error barrepresents standard error. (A) Dataset prediction accuracies for matched ADNI and AIBL participants. (B) Dataset prediction accuracies for matched ADNI and MACCparticipants.

图 11. 不同样本大小下，ComBat 和 DeepResBat 的数据集预测准确率。每次采样重复 50 次。误差条表示标准误差。(A) 匹配的 ADNI 和 AIBL 参与者的数据集预测准确率。(B) 匹配的 ADNI 和 MACC 参与者的数据集预测准确率。

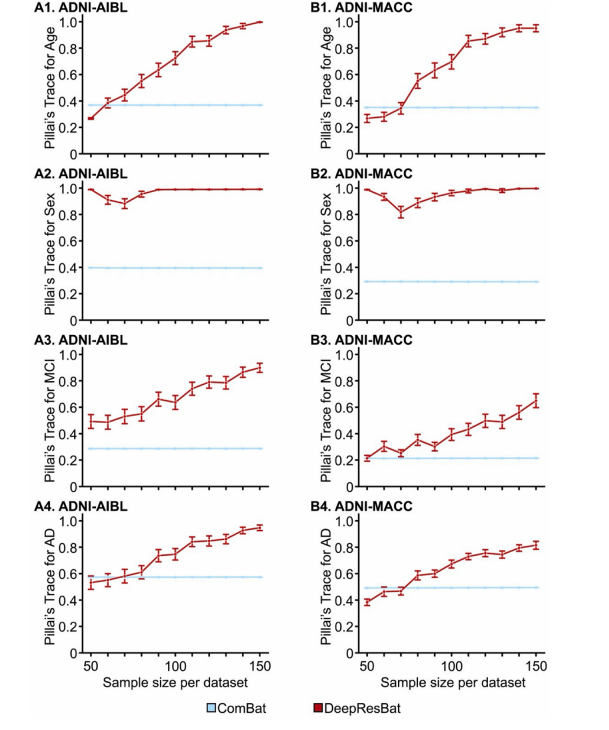
Fig. 12. Effect sizes of MANOVA involving clinical diagnosis for ComBat and DeepResBat with different sample size per dataset. Each sampling was repeated50 times. Error bar corresponds to the standard error. Left column shows the results for harmonizing ADNI and AIBL datasets. Right column shows the results forharmonizing ADNI and MACC datasets. First row corresponds to age associations. Second row corresponds to sex associations. Third row corresponds to MCI associations. Fourth row corresponds to AD diagnosis associations.

图 12. 不同样本大小下，ComBat 和 DeepResBat 的 MANOVA 临床诊断效应量。每次采样重复 50 次。误差条表示标准误差。左列显示的是用于协调 ADNI 和 AIBL 数据集的结果。右列显示的是用于协调 ADNI 和 MACC 数据集的结果。第一行对应年龄关联。第二行对应性别关联。第三行对应 MCI 关联。第四行对应 AD 诊断关联。

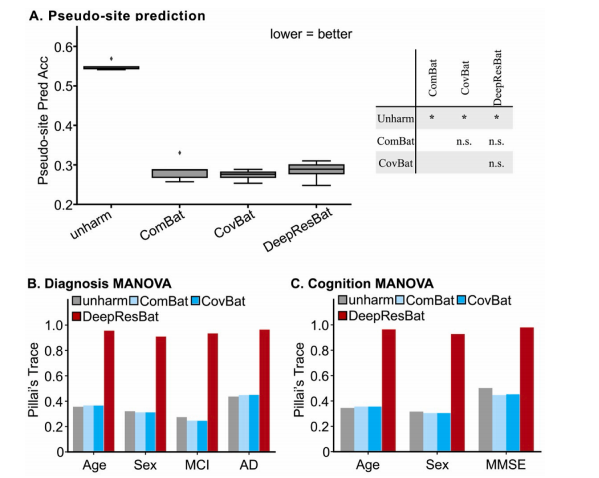
Fig. 13. Harmonization of many sites. (A) Dataset prediction accuracies across five folds. Corrected resampled t-test was used as a statistical test to comparedifferent approaches. (B) Effect size of MANOVA involving clinical diagnosis. (C) Effect size of MANOVA involving MMSE. A larger Pillai’s Trace indicates a strongerassociation, and thus better performance.

图 13. 多站点数据协调。(A) 五折交叉验证下的数据集预测准确率。使用修正的重采样 t 检验作为统计测试来比较不同的方法。(B) 涉及临床诊断的 MANOVA 效应量。(C) 涉及 MMSE 的 MANOVA 效应量。较大的 Pillai’s Trace 表示较强的关联，从而表明更好的性能。

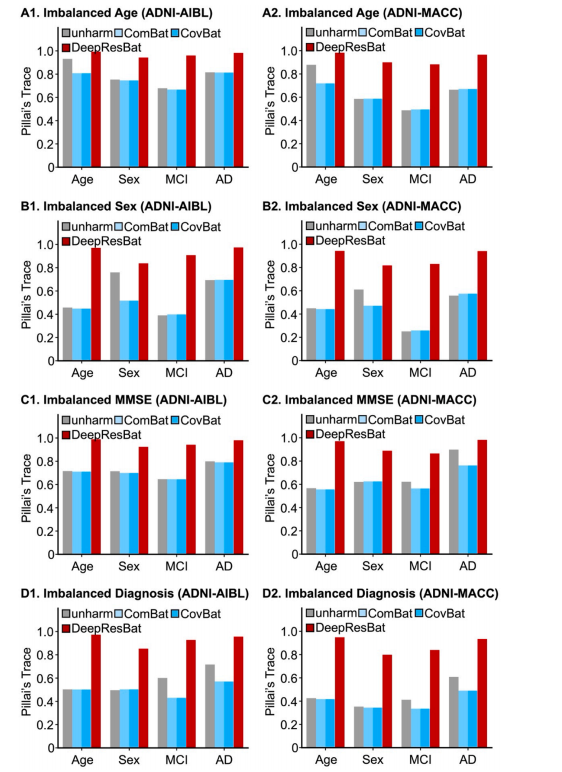
Fig. 14. Effect size of MANOVA involving clinical diagnosis in test sets involving highly imbalanced covariate distributions. A larger Pillai’s Trace indicatesa stronger association, and thus better performance. The left column corresponding to harmonizing ADNI and AIBL. The right column corresponding to harmonizingADNI and MACC. (A1) MANOVA effect sizes for ADNI-AIBL test set with highly imbalanced age distributions. (A2) Same as A1 but for ADNI and MACC. (B1)MANOVA effect sizes for ADNI-AIBL test set with highly imbalanced sex distributions. (B2) Same as B1 but for ADNI and MACC. (C1) MANOVA effect sizes for ADNIAIBL test set with highly imbalanced MMSE distributions. (C2) Same as C1 but for ADNI and MACC. (D1) MANOVA effect sizes for ADNI-AIBL test set with highlyimbalanced diagnosis distributions. (D2) Same as B1 but for ADNI and MACC. Note that there is only one number (effect size) for each covariate and harmonization approach.

图 14. 测试集中的临床诊断 MANOVA 效应量，涉及高度不平衡的协变量分布。较大的 Pillai’s Trace 表示较强的关联，从而表明更好的性能。左列对应协调 ADNI 和 AIBL 数据集，右列对应协调 ADNI 和 MACC 数据集。(A1) ADNI-AIBL 测试集，在高度不平衡的年龄分布下的 MANOVA 效应量。(A2) 同 A1，但针对 ADNI 和 MACC 数据集。(B1) ADNI-AIBL 测试集，在高度不平衡的性别分布下的 MANOVA 效应量。(B2) 同 B1，但针对 ADNI 和 MACC 数据集。(C1) ADNI-AIBL 测试集，在高度不平衡的 MMSE 分布下的 MANOVA 效应量。(C2) 同 C1，但针对 ADNI 和 MACC 数据集。(D1) ADNI-AIBL 测试集，在高度不平衡的诊断分布下的 MANOVA 效应量。(D2) 同 D1，但针对 ADNI 和 MACC 数据集。请注意，每个协变量和协调方法只有一个效应量（数值）。

Table

表

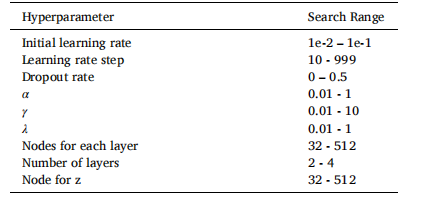
Table 1Hyperparameters search ranges for cVAE on the validationset. We note that a learning rate decay strategy was utilized.After K training epochs (where K = learning rate step), thelearning rate was reduced by a factor of 10.

表 1cVAE 在验证集上的超参数搜索范围。我们注意到，使用了学习率衰减策略。经过 K 次训练周期（其中 K 为学习率衰减步长），学习率会降低一个数量级。

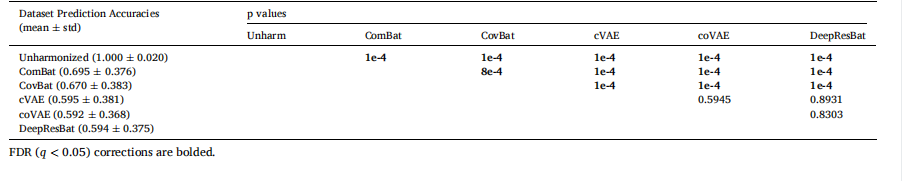
Table 2Dataset prediction accuracies with p values of differences between different approaches for matched ADNI and AIBL participants. Statistically significant p values after.

表 2 匹配的 ADNI 和 AIBL 参与者之间不同方法的数据集预测准确率及其差异的 p 值。统计学上显著的 p 值在 FDR 校正后标出。

Table 3Dataset prediction accuracies with p values of differences between different approaches for matched ADNI and MACC participants. Statistically significant p valuesafter.

表 3 匹配的 ADNI 和 MACC 参与者之间不同方法的数据集预测准确率及其差异的 p 值。统计学上显著的 p 值在 FDR 校正后标出。

原文地址：https://blog.csdn.net/weixin_38594676/article/details/144063280

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！