leetcode 3244. 新增道路查询后的最短距离 II

给你一个整数 n 和一个二维整数数组 queries。

有 n 个城市，编号从 0 到 n - 1。初始时，每个城市 i 都有一条单向道路通往城市 i + 1（ 0 <= i < n - 1）。

queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后，你需要找到从城市 0 到城市 n - 1 的最短路径的长度。

所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

返回一个数组 answer，对于范围 [0, queries.length - 1] 中的每个 i，answer[i] 是处理完前 i + 1 个查询后，从城市 0 到城市 n - 1 的最短路径的长度。

示例 1：

输入： n = 5, queries = [[2, 4], [0, 2], [0, 4]]

输出： [3, 2, 1]

解释：

新增一条从 2 到 4 的道路后，从 0 到 4 的最短路径长度为 3。

新增一条从 0 到 2 的道路后，从 0 到 4 的最短路径长度为 2。

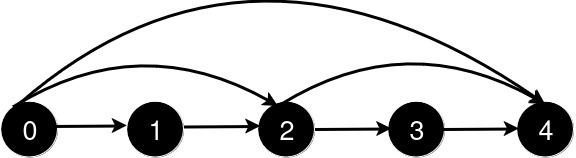
新增一条从 0 到 4 的道路后，从 0 到 4 的最短路径长度为 1。

示例 2：

输入： n = 4, queries = [[0, 3], [0, 2]]

输出： [1, 1]

解释：

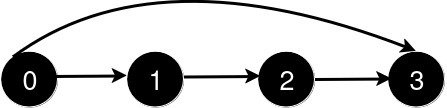
新增一条从 0 到 3 的道路后，从 0 到 3 的最短路径长度为 1。

新增一条从 0 到 2 的道路后，从 0 到 3 的最短路径长度仍为 1。

提示:

• 3 <= n <= 10e5
• 1 <= queries.length <= 10e5
• queries[i].length == 2
• 0 <= queries[i][0] < queries[i][1] < n
• 1 < queries[i][1] - queries[i][0]
• 查询中不存在重复的道路。
• 不存在两个查询都满足 i != j 且 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

分析：由题意，可知不存在两条交叉的路径，比如从1~3，从2~4.

我们可以贪心地选择最短路径经过的单向道路。具体地，初始时所有单向道路都是互不包含的关系，那么选择所有单向道路是最优的，最短路径的长度 dist=n−1 ，即为所有单向道路的数目。当我们新增一条单向道路时：

如果它已经被任一现有的单向道路所包含，那么选择它不会使路径更短，直接忽略它。

否则，我们去掉所有被新增单向道路所包含的现有单向道路，记数目为 m，然后将该新增单向道路加入最短路径中，此时最短路径的长度更新为 dist−m+1。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* shortestDistanceAfterQueries(int n, int** queries, int queriesSize, int* queriesColSize, int* returnSize) {
    int *ans=(int*)malloc(sizeof(int)*queriesSize);
    *returnSize=queriesSize;
    memset(ans,0,sizeof(int)*queriesSize);
    int temp_ans=n-1,t=0;//初始化答案为n-1

    int path[100010]={0};//path数组代表第i个城市的下一站为path[i]
    for(int i=0;i<n;++i)
        path[i]=i+1;//初始时编号为i的城市的下一站为i+1
    for(int i=0;i<queriesSize;++i)
    {
        //每次更新时把路径上的其它城市全部标记为-1
        //如新增1~3，则把path[2]更新为-1，因为不需要再从城市2经过了
        //注意每次更新的区间是(start,end)开区间

        int start=queries[i][0],end=queries[i][1],k=path[start],cnt=0;
        if(path[start]!=-1)path[start]=end;//
        while(k!=-1&&k<end)
        {
            int temp=path[k];
            path[k]=-1,k=temp,cnt++;
        }
        temp_ans-=cnt;
        ans[t++]=temp_ans;
    }

    return ans;
}

原文地址：https://blog.csdn.net/2401_88085478/article/details/143926923

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！