本文为对目前线性量化优点、原理、方法和实战内容的总结,主要参考 神经网络量化简介 并加以自己的理解和总结,适合初学者阅读和自身复习用。
1,模型量化概述
1.1,模型量化优点
模型量化是指将神经网络的浮点算法转换为定点。量化有一些相似的术语,低精度(Low precision)可能是常见的。
- 低精度模型表示模型权重数值格式为
FP16(半精度浮点)或者INT8(8位的定点整数),但是目前低精度往往就指代INT8。 - 常规精度模型则一般表示模型权重数值格式为
FP32(32位浮点,单精度)。 - 混合精度(Mixed precision)则在模型中同时使用
FP32和FP16的权重数值格式。FP16减少了一半的内存大小,但有些参数或操作符必须采用FP32格式才能保持准确度。
模型量化有以下好处:
- 减小模型大小:如
int8量化可减少75%的模型大小,int8量化模型大小一般为32位浮点模型大小的1/4:- 减少存储空间:在端侧存储空间不足时更具备意义。
- 减少内存占用:更小的模型当然就意味着不需要更多的内存空间。
- 减少设备功耗:内存耗用少了推理速度快了自然减少了设备功耗;
- 加快推理速度,访问一次
32位浮点型可以访问四次int8整型,整型运算比浮点型运算更快;CPU用int8计算的速度更快 - 某些硬件加速器如 DSP/NPU 只支持 int8。比如有些微处理器属于
8位的,低功耗运行浮点运算速度慢,需要进行8bit量化。
总结:模型量化主要意义就是加快模型端侧的推理速度,并降低设备功耗和减少存储空间,
工业界一般只使用 INT8 量化模型,如 NCNN、TNN 等移动端模型推理框架都支持模型的 INT8 量化和量化模型的推理功能。
通常,可以根据 FP32 和 INT8 的转换机制对量化模型推理方案进行分类。一些框架简单地引入了 Quantize 和 Dequantize 层,当从卷积或全链接层送入或取出时,它将 FP32 转换为 INT8 或相反。在这种情况下,如下图的上半部分所示,模型本身和输入/输出采用 FP32 格式。深度学习推理框架加载模型时,重写网络以插入 Quantize 和 Dequantize 层,并将权重转换为 INT8 格式。
注意,之所以要插入反量化层(
Dequantize),是因为量化技术的早期,只有卷积算子支持量化,但实际网络中还包含其他算子,而其他算子又只支持FP32计算,因此需要把 INT8 转换成 FP32。但随着技术的迭代,后期估计会逐步改善乃至消除Dequantize操作,达成全网络的量化运行,而不是部分算子量化运行。

图四:混合 FP32/INT8 和纯 INT8 推理。红色为 FP32,绿色为 INT8 或量化。
其他一些框架将网络整体转换为 INT8 格式,因此在推理期间没有格式转换,如上图的下半部分。该方法要求算子(Operator)都支持量化,因为运算符之间的数据流是 INT8。对于尚未支持的那些,它可能会回落到 Quantize/Dequantize 方案。
1.2,模型量化的方案
在实践中将浮点模型转为量化模型的方法有以下三种方法:
data free:不使用校准集,传统的方法直接将浮点参数转化成量化数,使用上非常简单,但是一般会带来很大的精度损失,但是高通最新的论文DFQ不使用校准集也得到了很高的精度。calibration:基于校准集方案,通过输入少量真实数据进行统计分析。很多芯片厂商都提供这样的功能,如tensorRT、高通、海思、地平线、寒武纪finetune:基于训练finetune的方案,将量化误差在训练时仿真建模,调整权重使其更适合量化。好处是能带来更大的精度提升,缺点是要修改模型训练代码,开发周期较长。
TensorFlow 框架按照量化阶段的不同,其模型量化功能分为以下两种:
- Post-training quantization
PTQ(训练后量化、离线量化); - Quantization-aware training
QAT(训练时量化,伪量化,在线量化)。
1.2.1,PTQ 理解
PTQ Post Training Quantization 是训练后量化,也叫做离线量化,根据量化零点 xzero_point 是否为 0,训练后量化分为对称量化和非对称量化;根据数据通道顺序 NHWC(TensorFlow) 这一维度区分,训练后量化又分为逐层量化和逐通道量化。目前 nvidia 的 TensorRT 框架中使用了逐层量化的方法,每一层采用同一个阈值来进行量化。逐通道量化就是对每一层每个通道都有各自的阈值,对精度可以有一个很好的提升。
1.3,量化的分类
目前已知的加快推理速度概率较大的量化方法主要有:
- 二值化,其可以用简单的位运算来同时计算大量的数。对比从 nvdia gpu 到 x86 平台,1bit 计算分别有 5 到128倍的理论性能提升。且其只会引入一个额外的量化操作,该操作可以享受到 SIMD(单指令多数据流)的加速收益。
- 线性量化(最常见),又可细分为非对称,对称和
ristretto几种。在nvdia gpu,x86、arm和 部分AI芯片平台上,均支持8bit的计算,效率提升从1倍到16倍不等,其中tensor core甚至支持4bit计算,这也是非常有潜力的方向。线性量化引入的额外量化/反量化计算都是标准的向量操作,因此也可以使用SIMD进行加速,带来的额外计算耗时不大。 - 对数量化,一种比较特殊的量化方法。两个同底的幂指数进行相乘,那么等价于其指数相加,降低了计算强度。同时加法也被转变为索引计算。目前
nvdia gpu,x86、arm三大平台上没有实现对数量化的加速库,但是目前已知海思351X系列芯片上使用了对数量化。
1.3.1,线性量化概述
与非线性量化不同,线性量化采用均匀分布的聚类中心,原始浮点数据和量化后的定点数据存在一个简单的线性变换关系,因为卷积、全连接等网络层本身只是简单的线性计算,因此线性量化中可以直接用量化后的数据进行直接计算。
2,量化算术
模型量化过程可以分为两部分:将模型从 FP32 转换为 INT8,以及使用 INT8 进行推理。本节说明这两部分背后的算术原理。如果不了解基础算术原理,在考虑量化细节时通常会感到困惑。
2.1,定点和浮点
定点和浮点都是数值的表示(representation),它们区别在于,将整数(integer)部分和小数(fractional)部分分开的点,点在哪里。定点保留特定位数整数和小数,而浮点保留特定位数的有效数字(significand)和指数(exponent)。
绝大多数现代的计算机系统采纳了浮点数表示方式,这种表达方式利用科学计数法来表达实数。即用一个尾数(Mantissa,尾数有时也称为有效数字,它实际上是有效数字的非正式说法),一个基数(Base),一个指数(Exponent)以及一个表示正负的符号来表达实数。具体组成如下:
- 第一部分为
sign符号位 s,占 1 bit,用来表示正负号; - 第二部分为
exponent指数偏移值 k,占 8 bits,用来表示其是 2 的多少次幂; - 第三部分是
fraction分数值(有效数字) M,占 23 bits,用来表示该浮点数的数值大小。
基于上述表示,浮点数的值可以用以下公式计算:
值得注意是,上述公式隐藏了一些细节,如指数偏移值 k 使用的时候需要加上一个固定的偏移值。
比如 123.45 用十进制科学计数法可以表示为 1.2345×102,其中 1.2345 为尾数,10 为基数,2 为指数。
单精度浮点类型 float 占用 32bit,所以也称作 FP32;双精度浮点类型 double 占用 64bit。
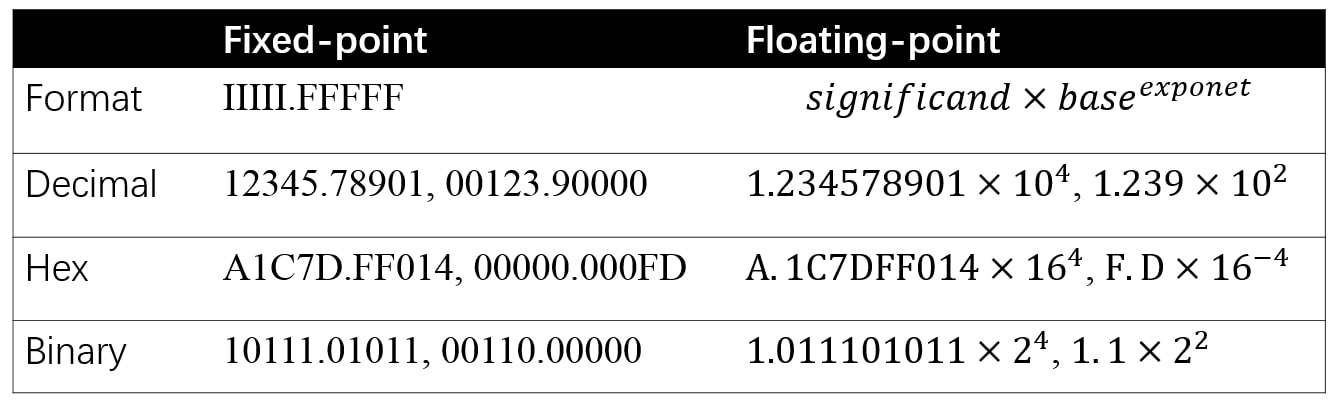
图五:定点和浮点的格式和示例。
2.2,量化浮点
32-bit 浮点数和 8-bit 定点数的表示范围如下表所示:
| 数据类型 | 最小值 | 最大值 |
|---|---|---|
FP32 | -3.4e38 | 3.4e38 |
int8 | -128 | 128 |
uint8 | 0 | 255 |
神经网络的推理由浮点运算构成。FP32 和 INT8 的值域是 [(2−223)×2127,(223−2)×2127] 和 [−128,127],而取值数量大约分别为 232 和 28 。FP32 取值范围非常广,因此,将网络从 FP32 转换为 INT8 并不像数据类型转换截断那样简单。但是,一般神经网络权重的值分布范围很窄,非常接近零。图八给出了 MobileNetV1 中十层(拥有最多值的层)的权重分布。
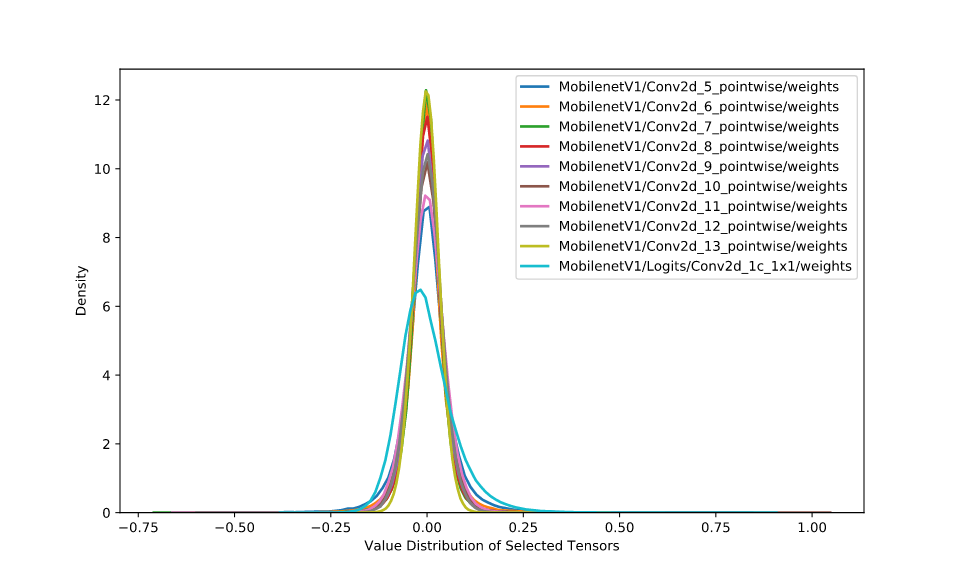
图八:十层 MobileNetV1 的权重分布。
根据偏移量 Z 是否为 0,可以将浮点数的线性量化分为两类-对称量化和非对称量化。
当浮点值域落在 (−1,1) 之间,权重浮点数据的量化运算可使用下式的方法将 FP32 映射到 INT8,这是对称量化。其中 xfloat 表示 FP32 权重, xquantized 表示量化的 INT8 权重,xscale 是缩放因子(映射因子、量化尺度(范围)/ float32 的缩放因子)。
对称量化的浮点值和 8 位定点值的映射关系如下图,从图中可以看出,对称量化就是将一个 tensor 中的 [−max(|x|),max(|x|)] 内的 FP32 值分别映射到 8 bit 数据的 [-128, 127] 的范围内,中间值按照线性关系进行映射,称这种映射关系是对称量化。可以看出,对称量化的浮点值和量化值范围都是相对于零对称的。
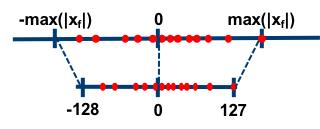
因为对称量化的缩放方法可能会将 FP32 零映射到 INT8 零,但我们不希望这种情况出现,于是出现了数字信号处理中的均一量化,即非对称量化。数学表达式如下所示,其中 xzero_point 表示量化零点(量化偏移)。
大多数情况下量化是选用无符号整数,即 INT8 的值域就为 [0,255] ,这种情况,显然要用非对称量化。非对称量化的浮点值和 8 位定点值的映射关系如下图:
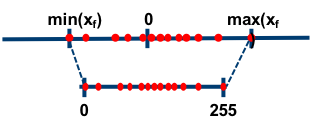
总的来说,权重量化浮点值可以分为两个步骤:
- 通过在权重张量(Tensor)中找到 min 和 max 值从而确定 xscale 和xzero_point。
- 将权重张量的每个值从 FP32 转换为 INT8 。
注意,当浮点运算结果不等于整数时,需要额外的舍入步骤。例如将 FP32 值域 [−1,1] 映射到 INT8 值域 [0,255],有 xscale=2255,而xzero_point=255−2552≈127。
注意,量化过程中存在误差是不可避免的,就像数字信号处理中量化一样。非对称算法一般能够较好地处理数据分布不均匀的情况。
2.2,量化算术
量化的一个重要议题是用量化算术表示非量化算术,即量化神经网络中的 INT8 计算是描述常规神经网络的 FP32 计算,对应的就是反量化过程,也就是如何将 INT8 的定点数据反量化成 FP32 的浮点数据。
下面的等式 5-10 是反量化乘法 xfloat⋅yfloat 的过程。对于给定神经网络,输入 x、权重 y 和输出 z 的缩放因子肯定是已知的,因此等式 14 的 Multiplierx,y,z=xscaleyscalezscale 也是已知的,在反量化过程之前可预先计算。因此,除了 Multiplierx,y,z 和 (xquantized−xzero_point)⋅(yquantized−yzero_point) 之间的乘法外,等式 16 中的运算都是整数运算。
等式:反量化算术过程。
对于等式 10 可以应用的大多数情况,quantized 和 zero_point 变量 (x,y) 都是 INT8 类型,scale 是 FP32。实际上两个 INT8 之间的算术运算会累加到 INT16 或 INT32,这时 INT8 的值域可能无法保存运算结果。例如,对于 xquantized=20、xzero_point=50 的情况,有
