用 Python 从零开始创建神经网络(十四):L1 和 L2 正则化(L1 and L2 Regularization)
L1 和 L2 正则化(L1 and L2 Regularization)
引言
正则化方法旨在降低泛化误差。我们首先讨论的正则化形式是L1正则化和L2正则化。L1和L2正则化用于计算一个数值(称为惩罚项),将其添加到损失值中,以惩罚模型中权重和偏置过大的情况。过大的权重可能表明某个神经元试图记忆数据元素;一般认为,让多个神经元共同对模型输出做出贡献要比依赖少数几个神经元更好。
1. Forward Pass
L1正则化的惩罚项是所有权重和偏置绝对值的总和。这是一种线性惩罚,因为这种正则化函数返回的损失值与参数值成正比。而L2正则化的惩罚项是所有权重和偏置平方值的总和。这种非线性方法因为使用平方函数来计算结果,对较大的权重和偏置施加了比小权重和偏置更大的惩罚。换句话说,L2正则化通常被使用,因为它对小参数值的影响不大,并通过对相对较大的值施加较重的惩罚,防止模型权重增长过大。而L1正则化由于其线性性质,对小权重的惩罚比L2正则化更大,从而使得模型对小输入值的响应逐渐不敏感,仅对较大的输入值敏感。因此,L1正则化很少单独使用,通常是在需要时与L2正则化结合使用。
这类正则化函数会推动权重和参数总和接近0,这在处理梯度爆炸(模型不稳定性导致权重变为非常大的值)时也有帮助。此外,我们还需要控制这种正则化惩罚的影响程度。我们在方程中引入一个被称为lambda的值,较大的lambda值意味着更大的惩罚。
L1权重正则化公式:
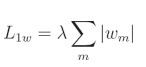
L1偏置正则化公式:
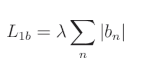
L2权重正则化公式:
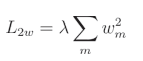
L2偏置正则化公式:
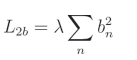
总体损失:
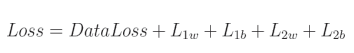
使用代码符号:
l1w = lambda_l1w * sum(abs(weights))
l1b = lambda_l1b * sum(abs(biases))
l2w = lambda_l2w * sum(weights**2)
l2b = lambda_l2b * sum(biases**2)
loss = data_loss + l1w + l1b + l2w + l2b
正则化损失是单独计算的,然后与数据损失相加,形成总体损失。参数 m m m 是遍历模型中所有权重的任意迭代器,参数 n n n 是遍历偏置的等效迭代器, w m w_m wm 是给定的权重, b n b_n bn 是给定的偏置。
为了在神经网络代码中实现正则化,我们将从 Dense 层类的 __init__ 方法开始,该方法将包含正则化强度超参数
λ
\lambda
λ,因为这些参数可以为每一层单独设置:
# Layer initialization
def __init__(self, inputs, neurons,
weight_regularizer_l1=0, weight_regularizer_l2=0,
bias_regularizer_l1=0, bias_regularizer_l2=0):
# Initialize weights and biases
self.weights = 0.01 * np.random.randn(inputs, neurons)
self.biases = np.zeros((1, neurons))
# Set regularization strength
self.weight_regularizer_l1 = weight_regularizer_l1
self.weight_regularizer_l2 = weight_regularizer_l2
self.bias_regularizer_l1 = bias_regularizer_l1
self.bias_regularizer_l2 = bias_regularizer_l2
该方法设置了
λ
\lambda
λ 超参数。现在我们更新损失类,以包括附加的惩罚项(如果我们选择在层的初始化中为任何正则化器设置
λ
\lambda
λ 超参数)。我们将在 Loss 类中实现此代码,因为它通常适用于隐藏层。此外,正则化计算是相同的,无论使用何种类型的损失函数。正则化仅仅是一个与数据损失值相加的惩罚项,从而得到最终的总体损失值。因此,我们将在通用损失类中添加一个新方法,该类由我们所有具体的损失函数(例如现有的 Loss_CategoricalCrossentropy)继承。
对于该方法的代码,我们将创建层的正则化损失变量。如果对应的 λ \lambda λ 值大于 0,我们会将每个原子正则化损失添加到该变量中。为了执行这些计算,我们将从传入的层对象中读取 λ \lambda λ 超参数、权重和偏置。对于我们的通用损失类:
# Regularization loss calculation
def regularization_loss(self, layer):
# 0 by default
regularization_loss = 0
# L1 regularization - weights
# calculate only when factor greater than 0
if layer.weight_regularizer_l1 > 0:
regularization_loss += layer.weight_regularizer_l1 * np.sum(np.abs(layer.weights))
# L2 regularization - weights
if layer.weight_regularizer_l2 > 0:
regularization_loss += layer.weight_regularizer_l2 * np.sum(layer.weights * layer.weights)
# L1 regularization - biases
# calculate only when factor greater than 0
if layer.bias_regularizer_l1 > 0:
regularization_loss += layer.bias_regularizer_l1 * np.sum(np.abs(layer.biases))
# L2 regularization - biases
if layer.bias_regularizer_l2 > 0:
regularization_loss += layer.bias_regularizer_l2 * np.sum(layer.biases * layer.biases)
return regularization_loss
然后,我们将计算正则化损失,并将其添加到训练循环中计算出的损失中:
# Calculate loss from output of activation2 so softmax activation
data_loss = loss_function.forward(activation2.output, y)
# Calculate regularization penalty
regularization_loss = loss_function.regularization_loss(dense1) + loss_function.regularization_loss(dense2)
# Calculate overall loss
loss = data_loss + regularization_loss
我们创建了一个新的变量 regularization_loss,并将所有层的正则化损失添加到了该变量中。这完成了正则化的前向传播部分,但这也意味着我们的总体损失发生了变化,因为计算的一部分可能包括正则化,这在反向传播梯度时必须加以考虑。因此,我们接下来将介绍
L
1
L1
L1 和
L
2
L2
L2 正则化的偏导数。
2. Backward pass
L2 正则化的导数相对简单:
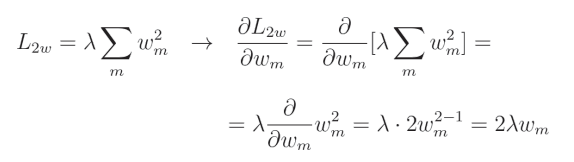
这看起来可能很复杂,但实际上是本书中需要推导的较为简单的导数之一。由于
λ
\lambda
λ 是常数,因此我们可以将其移出导数项之外。我们可以去掉求和符号,因为我们仅计算针对给定参数的偏导数,而单个元素的求和等于其自身。因此,我们只需要计算
w
2
w^2
w2 的导数,我们知道其导数为
2
w
2w
2w。从编码的角度看,我们只需将所有权重乘以
2
λ
2\lambda
2λ。我们将直接使用 NumPy 来实现这一点,因为这仅是一个简单的乘法操作。
另一方面, L 1 L1 L1 正则化的导数需要更多的解释。在 L 1 L1 L1 正则化的情况下,我们必须分段计算绝对值函数的导数,这实际上是将值乘以 − 1 -1 −1(如果值小于 0),否则乘以 1 1 1。这是因为绝对值函数对于正值是线性的,而我们知道线性函数的导数为:
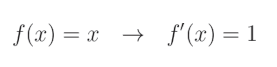
对于负值,它会将值的符号取反以使其变为正值。换句话说,它将值乘以 − 1 -1 −1:
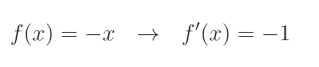
当我们把这些结合起来:
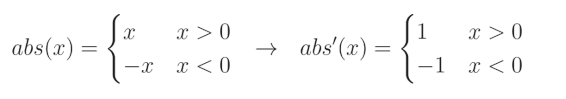
以及
L
1
L1
L1 正则化关于给定权重的完全偏导数:
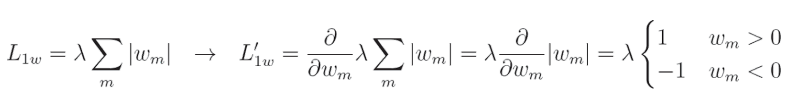
像 L 2 L2 L2正则化一样, λ \lambda λ是一个常数,我们计算该正则化相对于特定输入的偏导数。在这种情况下,偏导数等于1或 − 1 -1 −1,具体取决于 w m w_m wm(权重)的值。
我们正在对权重计算这个偏导数,并将得到的梯度用于更新权重。这个梯度与权重的形状相同。用纯Python代码表达如下:
weights = [0.2, 0.8, -0.5] # weights of one neuron
dL1 = [] # array of partial derivatives of L1 regularization
for weight in weights:
if weight >= 0:
dL1.append(1)
else:
dL1.append(-1)
print(dL1)
>>>
[1, 1, -1]
你可能注意到,我们在代码中使用的是
≥
0
\geq 0
≥0,而上面的公式显然描述的是
>
0
> 0
>0。如果我们观察np.abs函数,它的图像是一条向下的直线,在值为
0
0
0的位置“反弹”,类似锯齿的形状。在尖端(即值为
0
0
0的位置),np.abs函数的导数是未定义的,但我们无法以这种方式编码,因此我们需要处理这种情况,并稍微违反一下规则。
现在,让我们尝试修改这个 L 1 L1 L1,导数,使其可以处理一个层中的多个神经元:
weights = [[0.2, 0.8, -0.5, 1], # now we have 3 sets of weights
[0.5, -0.91, 0.26, -0.5],
[-0.26, -0.27, 0.17, 0.87]]
dL1 = [] # array of partial derivatives of L1 regularization
for neuron in weights:
neuron_dL1 = [] # derivatives related to one neuron
for weight in neuron:
if weight >= 0:
neuron_dL1.append(1)
else:
neuron_dL1.append(-1)
dL1.append(neuron_dL1)
print(dL1)
>>>
[[1, 1, -1, 1], [1, -1, 1, -1], [-1, -1, 1, 1]]
这是原生Python版本的实现,现在使用NumPy实现。借助NumPy,我们将使用条件和二进制掩码来实现。我们将创建一个梯度数组,其值全部为1,并且形状与权重相同,使用np.ones_like(weights)。接着,条件weights < 0将返回一个与dL1形状相同的数组,其中条件为假时值为0,为真时值为1。我们将其作为dL1的二进制掩码,仅在条件为真时(权重值小于0)将值设置为-1:
import numpy as np
weights = np.array([[0.2, 0.8, -0.5, 1],
[0.5, -0.91, 0.26, -0.5],
[-0.26, -0.27, 0.17, 0.87]])
dL1 = np.ones_like(weights)
dL1[weights < 0] = -1
print(dL1)
>>>
[[ 1. 1. -1. 1.]
[ 1. -1. 1. -1.]
[-1. -1. 1. 1.]]
这段代码返回了一个与原始权重形状相同的数组,包含值1和-1——这是对np.abs函数的偏导数梯度(我们仍然需要将其乘以lambda超参数)。现在,我们可以使用这些值来更新密集层对象的反向传播方法。对于L1正则化,我们将上述代码乘以权重的
λ
\lambda
λ,并对偏置执行相同的操作。对于L2正则化,如本章开头所述,我们需要做的只是将权重/偏置乘以
2
λ
2\lambda
2λ,然后将这个结果加到梯度中:
# Dense layer
class Layer_Dense:
...
# Backward pass
def backward(self, dvalues):
# Gradients on parameters
self.dweights = np.dot(self.inputs.T, dvalues)
self.dbiases = np.sum(dvalues, axis=0, keepdims=True)
# Gradients on regularization
# L1 on weights
if self.weight_regularizer_l1 > 0:
dL1 = np.ones_like(self.weights)
dL1[self.weights < 0] = -1
self.dweights += self.weight_regularizer_l1 * dL1
# L2 on weights
if self.weight_regularizer_l2 > 0:
self.dweights += 2 * self.weight_regularizer_l2 * self.weights
# L1 on biases
if self.bias_regularizer_l1 > 0:
dL1 = np.ones_like(self.biases)
dL1[self.biases < 0] = -1
self.dbiases += self.bias_regularizer_l1 * dL1
# L2 on biases
if self.bias_regularizer_l2 > 0:
self.dbiases += 2 * self.bias_regularizer_l2 * self.biases
# Gradient on values
self.dinputs = np.dot(dvalues, self.weights.T)
这样,我们就可以更新我们的印刷品,加入新的信息–正则化损失和总体损失:
print(f'epoch: {epoch}, ' +
f'acc: {accuracy:.3f}, ' +
f'loss: {loss:.3f} (' +
f'data_loss: {data_loss:.3f}, ' +
f'reg_loss: {regularization_loss:.3f}), ' +
f'lr: {optimizer.current_learning_rate}')
然后,我们可以在定义图层时添加权重和偏置正则参数:
# Create Dense layer with 2 input features and 3 output values
dense1 = Layer_Dense(2, 64, weight_regularizer_l2=5e-4, bias_regularizer_l2=5e-4)
我们通常只对隐藏层添加正则化项。即使我们也对输出层调用了正则化方法,如果我们没有将lambda超参数设置为非零值,正则化方法也不会修改梯度。
到此为止的全部代码:
import numpy as np
import nnfs
from nnfs.datasets import spiral_data
nnfs.init()
# Dense layer
class Layer_Dense:
# Layer initialization
def __init__(self, n_inputs, n_neurons,
weight_regularizer_l1=0, weight_regularizer_l2=0,
bias_regularizer_l1=0, bias_regularizer_l2=0):
# Initialize weights and biases
self.weights = 0.01 * np.random.randn(n_inputs, n_neurons)
self.biases = np.zeros((1, n_neurons))
# Set regularization strength
self.weight_regularizer_l1 = weight_regularizer_l1
self.weight_regularizer_l2 = weight_regularizer_l2
self.bias_regularizer_l1 = bias_regularizer_l1
self.bias_regularizer_l2 = bias_regularizer_l2
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs, weights and biases
self.output = np.dot(inputs, self.weights) + self.biases
# Backward pass
def backward(self, dvalues):
# Gradients on parameters
self.dweights = np.dot(self.inputs.T, dvalues)
self.dbiases = np.sum(dvalues, axis=0, keepdims=True)
# Gradients on regularization
# L1 on weights
if self.weight_regularizer_l1 > 0:
dL1 = np.ones_like(self.weights)
dL1[self.weights < 0] = -1
self.dweights += self.weight_regularizer_l1 * dL1
# L2 on weights
if self.weight_regularizer_l2 > 0:
self.dweights += 2 * self.weight_regularizer_l2 * self.weights
# L1 on biases
if self.bias_regularizer_l1 > 0:
dL1 = np.ones_like(self.biases)
dL1[self.biases < 0] = -1
self.dbiases += self.bias_regularizer_l1 * dL1
# L2 on biases
if self.bias_regularizer_l2 > 0:
self.dbiases += 2 * self.bias_regularizer_l2 * self.biases
# Gradient on values
self.dinputs = np.dot(dvalues, self.weights.T)
# ReLU activation
class Activation_ReLU:
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs
self.output = np.maximum(0, inputs)
# Backward pass
def backward(self, dvalues):
# Since we need to modify original variable,
# let's make a copy of values first
self.dinputs = dvalues.copy()
# Zero gradient where input values were negative
self.dinputs[self.inputs <= 0] = 0
# Softmax activation
class Activation_Softmax:
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Get unnormalized probabilities
exp_values = np.exp(inputs - np.max(inputs, axis=1, keepdims=True))
# Normalize them for each sample
probabilities = exp_values / np.sum(exp_values, axis=1, keepdims=True)
self.output = probabilities
# Backward pass
def backward(self, dvalues):
# Create uninitialized array
self.dinputs = np.empty_like(dvalues)
# Enumerate outputs and gradients
for index, (single_output, single_dvalues) in enumerate(zip(self.output, dvalues)):
# Flatten output array
single_output = single_output.reshape(-1, 1)
# Calculate Jacobian matrix of the output and
jacobian_matrix = np.diagflat(single_output) - np.dot(single_output, single_output.T)
# Calculate sample-wise gradient
# and add it to the array of sample gradients
self.dinputs[index] = np.dot(jacobian_matrix, single_dvalues)
# SGD optimizer
class Optimizer_SGD:
# Initialize optimizer - set settings,
# learning rate of 1. is default for this optimizer
def __init__(self, learning_rate=1., decay=0., momentum=0.):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.momentum = momentum
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If we use momentum
if self.momentum:
# If layer does not contain momentum arrays, create them
# filled with zeros
if not hasattr(layer, 'weight_momentums'):
layer.weight_momentums = np.zeros_like(layer.weights)
# If there is no momentum array for weights
# The array doesn't exist for biases yet either.
layer.bias_momentums = np.zeros_like(layer.biases)
# Build weight updates with momentum - take previous
# updates multiplied by retain factor and update with
# current gradients
weight_updates = self.momentum * layer.weight_momentums - self.current_learning_rate * layer.dweights
layer.weight_momentums = weight_updates
# Build bias updates
bias_updates = self.momentum * layer.bias_momentums - self.current_learning_rate * layer.dbiases
layer.bias_momentums = bias_updates
# Vanilla SGD updates (as before momentum update)
else:
weight_updates = -self.current_learning_rate * layer.dweights
bias_updates = -self.current_learning_rate * layer.dbiases
# Update weights and biases using either
# vanilla or momentum updates
layer.weights += weight_updates
layer.biases += bias_updates
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Adagrad optimizer
class Optimizer_Adagrad:
# Initialize optimizer - set settings
def __init__(self, learning_rate=1., decay=0., epsilon=1e-7):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_cache = np.zeros_like(layer.biases)
# Update cache with squared current gradients
layer.weight_cache += layer.dweights**2
layer.bias_cache += layer.dbiases**2
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * layer.dweights / (np.sqrt(layer.weight_cache) + self.epsilon)
layer.biases += -self.current_learning_rate * layer.dbiases / (np.sqrt(layer.bias_cache) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# RMSprop optimizer
class Optimizer_RMSprop:
# Initialize optimizer - set settings
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, rho=0.9):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
self.rho = rho
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_cache = np.zeros_like(layer.biases)
# Update cache with squared current gradients
layer.weight_cache = self.rho * layer.weight_cache + (1 - self.rho) * layer.dweights**2
layer.bias_cache = self.rho * layer.bias_cache + (1 - self.rho) * layer.dbiases**2
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * layer.dweights / (np.sqrt(layer.weight_cache) + self.epsilon)
layer.biases += -self.current_learning_rate * layer.dbiases / (np.sqrt(layer.bias_cache) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Adam optimizer
class Optimizer_Adam:
# Initialize optimizer - set settings
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, beta_1=0.9, beta_2=0.999):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
self.beta_1 = beta_1
self.beta_2 = beta_2
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_momentums = np.zeros_like(layer.weights)
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_momentums = np.zeros_like(layer.biases)
layer.bias_cache = np.zeros_like(layer.biases)
# Update momentum with current gradients
layer.weight_momentums = self.beta_1 * layer.weight_momentums + (1 - self.beta_1) * layer.dweights
layer.bias_momentums = self.beta_1 * layer.bias_momentums + (1 - self.beta_1) * layer.dbiases
# Get corrected momentum
# self.iteration is 0 at first pass
# and we need to start with 1 here
weight_momentums_corrected = layer.weight_momentums / (1 - self.beta_1 ** (self.iterations + 1))
bias_momentums_corrected = layer.bias_momentums / (1 - self.beta_1 ** (self.iterations + 1))
# Update cache with squared current gradients
layer.weight_cache = self.beta_2 * layer.weight_cache + (1 - self.beta_2) * layer.dweights**2
layer.bias_cache = self.beta_2 * layer.bias_cache + (1 - self.beta_2) * layer.dbiases**2
# Get corrected cache
weight_cache_corrected = layer.weight_cache / (1 - self.beta_2 ** (self.iterations + 1))
bias_cache_corrected = layer.bias_cache / (1 - self.beta_2 ** (self.iterations + 1))
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * weight_momentums_corrected / (np.sqrt(weight_cache_corrected) + self.epsilon)
layer.biases += -self.current_learning_rate * bias_momentums_corrected / (np.sqrt(bias_cache_corrected) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Common loss class
class Loss:
# Regularization loss calculation
def regularization_loss(self, layer):
# 0 by default
regularization_loss = 0
# L1 regularization - weights
# calculate only when factor greater than 0
if layer.weight_regularizer_l1 > 0:
regularization_loss += layer.weight_regularizer_l1 * np.sum(np.abs(layer.weights))
# L2 regularization - weights
if layer.weight_regularizer_l2 > 0:
regularization_loss += layer.weight_regularizer_l2 * np.sum(layer.weights * layer.weights)
# L1 regularization - biases
# calculate only when factor greater than 0
if layer.bias_regularizer_l1 > 0:
regularization_loss += layer.bias_regularizer_l1 * np.sum(np.abs(layer.biases))
# L2 regularization - biases
if layer.bias_regularizer_l2 > 0:
regularization_loss += layer.bias_regularizer_l2 * np.sum(layer.biases * layer.biases)
return regularization_loss
# Calculates the data and regularization losses
# given model output and ground truth values
def calculate(self, output, y):
# Calculate sample losses
sample_losses = self.forward(output, y)
# Calculate mean loss
data_loss = np.mean(sample_losses)
# Return loss
return data_loss
# Cross-entropy loss
class Loss_CategoricalCrossentropy(Loss):
# Forward pass
def forward(self, y_pred, y_true):
# Number of samples in a batch
samples = len(y_pred)
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)
# Probabilities for target values -
# only if categorical labels
if len(y_true.shape) == 1:
correct_confidences = y_pred_clipped[range(samples), y_true]
# Mask values - only for one-hot encoded labels
elif len(y_true.shape) == 2:
correct_confidences = np.sum(y_pred_clipped * y_true, axis=1)
# Losses
negative_log_likelihoods = -np.log(correct_confidences)
return negative_log_likelihoods
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of labels in every sample
# We'll use the first sample to count them
labels = len(dvalues[0])
# If labels are sparse, turn them into one-hot vector
if len(y_true.shape) == 1:
y_true = np.eye(labels)[y_true]
# Calculate gradient
self.dinputs = -y_true / dvalues
# Normalize gradient
self.dinputs = self.dinputs / samples
# Softmax classifier - combined Softmax activation
# and cross-entropy loss for faster backward step
class Activation_Softmax_Loss_CategoricalCrossentropy():
# Creates activation and loss function objects
def __init__(self):
self.activation = Activation_Softmax()
self.loss = Loss_CategoricalCrossentropy()
# Forward pass
def forward(self, inputs, y_true):
# Output layer's activation function
self.activation.forward(inputs)
# Set the output
self.output = self.activation.output
# Calculate and return loss value
return self.loss.calculate(self.output, y_true)
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# If labels are one-hot encoded,
# turn them into discrete values
if len(y_true.shape) == 2:
y_true = np.argmax(y_true, axis=1)
# Copy so we can safely modify
self.dinputs = dvalues.copy()
# Calculate gradient
self.dinputs[range(samples), y_true] -= 1
# Normalize gradient
self.dinputs = self.dinputs / samples
# Create dataset
X, y = spiral_data(samples=100, classes=3)
# Create Dense layer with 2 input features and 64 output values
dense1 = Layer_Dense(2, 64, weight_regularizer_l2=5e-4, bias_regularizer_l2=5e-4)
# Create ReLU activation (to be used with Dense layer):
activation1 = Activation_ReLU()
# Create second Dense layer with 64 input features (as we take output
# of previous layer here) and 3 output values (output values)
dense2 = Layer_Dense(64, 3)
# Create Softmax classifier's combined loss and activation
loss_activation = Activation_Softmax_Loss_CategoricalCrossentropy()
# Create optimizer
optimizer = Optimizer_Adam(learning_rate=0.02, decay=5e-7)
# Train in loop
for epoch in range(10001):
# Perform a forward pass of our training data through this layer
dense1.forward(X)
# Perform a forward pass through activation function
# takes the output of first dense layer here
activation1.forward(dense1.output)
# Perform a forward pass through second Dense layer
# takes outputs of activation function of first layer as inputs
dense2.forward(activation1.output)
# Perform a forward pass through the activation/loss function
# takes the output of second dense layer here and returns loss
data_loss = loss_activation.forward(dense2.output, y)
# Calculate regularization penalty
regularization_loss = loss_activation.loss.regularization_loss(dense1) + loss_activation.loss.regularization_loss(dense2)
# Calculate overall loss
loss = data_loss + regularization_loss
# Calculate accuracy from output of activation2 and targets
# calculate values along first axis
predictions = np.argmax(loss_activation.output, axis=1)
if len(y.shape) == 2:
y = np.argmax(y, axis=1)
accuracy = np.mean(predictions==y)
if not epoch % 100:
print(f'epoch: {epoch}, ' +
f'acc: {accuracy:.3f}, ' +
f'loss: {loss:.3f} (' +
f'data_loss: {data_loss:.3f}, ' +
f'reg_loss: {regularization_loss:.3f}), ' +
f'lr: {optimizer.current_learning_rate}')
# Backward pass
loss_activation.backward(loss_activation.output, y)
dense2.backward(loss_activation.dinputs)
activation1.backward(dense2.dinputs)
dense1.backward(activation1.dinputs)
# Update weights and biases
optimizer.pre_update_params()
optimizer.update_params(dense1)
optimizer.update_params(dense2)
optimizer.post_update_params()
# Validate the model
# Create test dataset
X_test, y_test = spiral_data(samples=100, classes=3)
# Perform a forward pass of our testing data through this layer
dense1.forward(X_test)
# Perform a forward pass through activation function
# takes the output of first dense layer here
activation1.forward(dense1.output)
# Perform a forward pass through second Dense layer
# takes outputs of activation function of first layer as inputs
dense2.forward(activation1.output)
# Perform a forward pass through the activation/loss function
# takes the output of second dense layer here and returns loss
loss = loss_activation.forward(dense2.output, y_test)
# Calculate accuracy from output of activation2 and targets
# calculate values along first axis
predictions = np.argmax(loss_activation.output, axis=1)
if len(y_test.shape) == 2:
y_test = np.argmax(y_test, axis=1)
accuracy = np.mean(predictions==y_test)
print(f'validation, acc: {accuracy:.3f}, loss: {loss:.3f}')
>>>
epoch: 10000, acc: 0.950, loss: 0.226 (data_loss: 0.165, reg_loss: 0.062), lr: 0.019900507413187767
validation, acc: 0.840, loss: 0.525

代码可视化:https://nnfs.io/abc
此动画展示了背景中的训练数据(暗淡的点)和前景中的验证数据。在向隐藏层添加L2正则化项后,我们实现了更低的验证损失(添加正则化前为0.858,现在为0.435)以及更高的准确率(添加正则化前为0.803,现在为0.830)。我们还可以花点时间举例说明简单增加训练数据量如何带来巨大差异。如果我们将样本量从100增加到1000:
# Create dataset
X, y = spiral_data(samples=1000, classes=3)
然后再次运行代码:
>>>
epoch: 10000, acc: 0.906, loss: 0.331 (data_loss: 0.273, reg_loss: 0.058), lr: 0.019900507413187767
validation, acc: 0.880, loss: 0.339

代码可视化:https://nnfs.io/bcd
我们可以看到,仅此更改也对整体验证准确率以及验证和训练准确率之间的差异产生了显著影响——较低的准确率和较高的训练损失表明模型的容量可能太低。之前较大的差异现在变小了,这表明模型之前很可能存在过拟合现象。从理论上讲,这种正则化允许我们创建更大的模型而不必担心过拟合(或记忆化)。我们可以通过增加每层的神经元数量来测试这一点。将每层神经元数量增加到128或256有助于提高训练准确率,但对验证准确率的提升并不显著:
# Create Dense layer with 2 input features and 256 output values
dense1 = Layer_Dense(2, 256, weight_regularizer_l2=5e-4, bias_regularizer_l2=5e-4)
# Create ReLU activation (to be used with Dense layer):
activation1 = Activation_ReLU()
# Create second Dense layer with 256 input features (as we take output
# of previous layer here) and 3 output values (output values)
dense2 = Layer_Dense(256, 3)
>>>
epoch: 10000, acc: 0.917, loss: 0.255 (data_loss: 0.215, reg_loss: 0.040), lr: 0.019900507413187767
validation, acc: 0.893, loss: 0.331
这并没有对结果产生多大影响,但将这一数字再次提高到 512 确实也提高了验证的准确性和损失:
# Create Dense layer with 2 input features and 256 output values
dense1 = Layer_Dense(2, 512, weight_regularizer_l2=5e-4, bias_regularizer_l2=5e-4)
# Create ReLU activation (to be used with Dense layer):
activation1 = Activation_ReLU()
# Create second Dense layer with 256 input features (as we take output
# of previous layer here) and 3 output values (output values)
dense2 = Layer_Dense(512, 3)
>>>
epoch: 10000, acc: 0.921, loss: 0.263 (data_loss: 0.214, reg_loss: 0.049), lr: 0.019900507413187767
validation, acc: 0.913, loss: 0.279

代码可视化:https://nnfs.io/cde
在这种情况下,我们可以看到样本内数据和样本外数据的准确率和损失几乎相同。从这里开始,我们可以添加更多的层和神经元,或者两者兼有。可以随意尝试调整,以进一步改进模型。接下来,我们将介绍另一种正则化方法:Dropout(随机失活)。
本章的章节代码、更多资源和勘误表:https://nnfs.io/ch13
原文地址:https://blog.csdn.net/xzs1210652636/article/details/144202441
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
