【蓝桥杯备赛】123（前缀和的复杂应用）

5. 前缀和的复杂应用

5.1. 123（4 星）

5.1.1. 题目解析

1. 这道题仍然是求一段区间的和，很容易能够想到前缀和
2. 找规律：

1------------------1 号块

1 2----------------2 号块

1 2 3--------------3 号块

1 2 3 4------------4 号块

1. 可以将其看做是若干个块，每个块内都是公差为 1 的等差数列
2. 我们只需要判断这个区间是第几号块，然后算出来当前的前缀和，使用之前的公式 s[r]-s[l-1]得到这段区间的和

来两道例子：

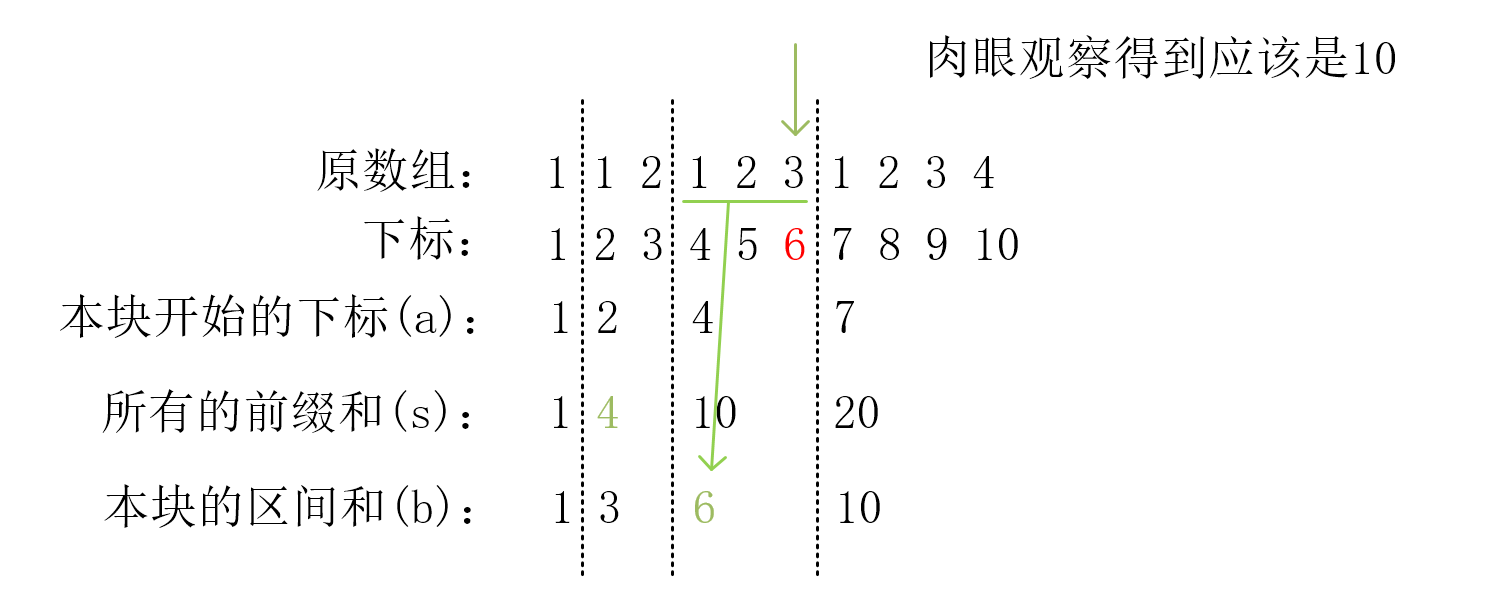
比如要求下标为 5 之前的前缀和。

我们可以根据规律求出这一块之前的前缀和，然后再根据它位于本块的第几位，求出应该在块区间和中的第几位，修正这个之前的前缀和。

详细过程：

1. 1. 要求的下标为 5，算出其在 4 下标开始的块中，因为 5 >= 4。（就是 a[3]=4）
   2. 这块之前的前缀和为 4，需要在 4 的基础上修正。（s[3-1]=4）
   3. 求出原数组中下标为 5 的数字，距离本块开头是 3 位，所以应该加上 1~3 的和 6。（6-a[3]+1=3，b[3] = 6）
   4. 4+6=10

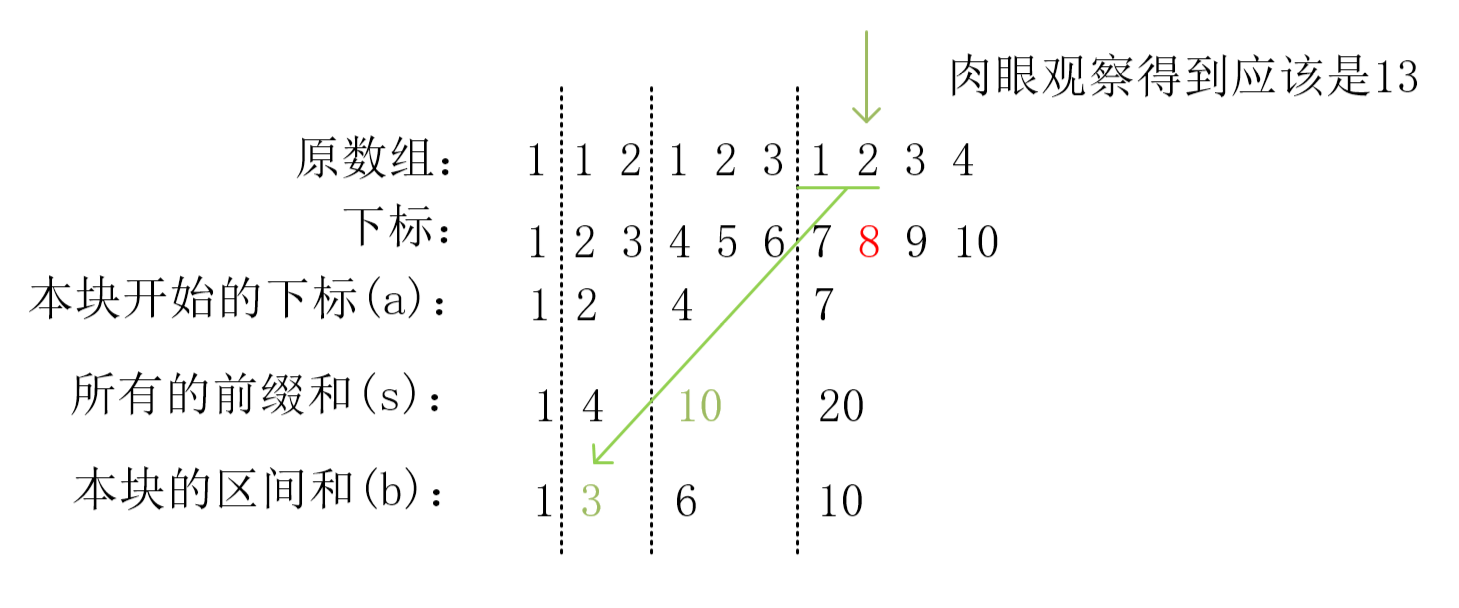
比如要求下标为 8 的前缀和。

1. 1. 求出这个在以 7 开头的块中，因为 8 >= 7。（a[4]=7）
   2. 这块之前的前缀和是 10，需要在 10 的基础上进行修正。（s[4-1]=10）
   3. 因为下标为 8，距离本块开头的距离为 2，所以需要加上 1~2 的和 3。（8-a[4]+1=2，b[2] = 3）
   4. 10+3=13

5.1.2. 代码

package lanqiao;

import java.util.Scanner;

public class _23_123 {
    static Scanner in = new Scanner(System.in);
    static int N = (int) (1e6 + 1e6 + 1e6);
    static long[] a = new long[N];// 区间开头的下标
    static long[] b = new long[N];// 每个区间的和
    static long[] s = new long[N];// 所有的前缀和

    public static void main(String[] args) {
        long t = in.nextLong();
        // 构建区间，前缀和
        a[0] = 1;
        for (int i = 1; i < N; i++) {
            a[i] = a[i - 1] + i;
            b[i] = b[i - 1] + i;
            s[i] = s[i - 1] + b[i];
        }

        // 查找l和r应该在哪个区间
        for (int i = 0; i < t; i++) {
            long l = in.nextLong(), r = in.nextLong();
            // 找>=x
            solve(l, r);
        }
    }

    private static void solve(long x, long y) {
        int l = 0, r = N - 1;
        // 找到l在哪个区间
        l = getL(x, l, r);
        // 开始坐标是a[l-1]，上一个区间结束的前缀和是s[l-1]，本区间的和是b[l-1]
        long gap = x - a[l];
//        System.out.print("l: " + l + " ");
//        System.out.print( (s[l] + x-a[l]));
        long q = s[l] + b[(int) gap];

        // 找到r在哪个区间
        l = 0;
        r = N - 1;
        l = getL(y, l, r);
        gap = y - a[l] + 1;
//        System.out.println();
//        System.out.print("l: " + l);
//        System.out.println(" " + (s[l] + y-a[l]));
        long w = s[l] + b[(int) gap];

        System.out.println(w - q);
//        System.out.println("------_");
    }

    private static int getL(long x, int l, int r) {
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (a[mid] > x) {
                r = mid - 1;
            } else {
                l = mid;
            }
        }
        return l;
    }
}

原文地址：https://blog.csdn.net/leadera_/article/details/143928649

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！