LeetCode 链表OJ题

1.消失的数字

题目信息及链接：面试题 17.04. 消失的数字 - 力扣（LeetCode） 

分析：

首先我们看到题目给予了我们一个数组，要求我们找到消失的数字，这个消失的数字指的是所给我们的数组中排序后少掉的数字，比方说示例1中给了最大数3，前面的数字应该是0，1，2，3，但是输入的却是3，0，1，缺少了数字2，那么2就是消失的数字。并且题目要求O(n)，意味着我们只可以遍历一遍数组。

思路考虑： 

既然它给我们的是缺失的数组，那么我们可以创建一个正常的数组，通过对双方数组元素的对比找出缺少的数字，但是这样的时间复杂度就是O(n^2)了，因为我们每次判断新正常数组中的元素都需要遍历原来缺失的数组一遍，这样的方法不太可行。

 那么有没有一种方法可以不用遍历两次呢？这时候我们就想到了位操作符 -> ^ 按位异或

// 我们知道按位异或的操作原理
// 相同为0，相异为1


    int a = 10;
    a ^ a = 0;
 0000 0000 0000 1010  - 10的补码
 0000 0000 0000 1010  - 10的补码


 0000 0000 0000 0000  - 按位异或后


    a ^ 0 = a;
 0000 0000 0000 1010  - 10的补码
 0000 0000 0000 0000  -  0的补码

 0000 0000 0000 1010  - 按位异或后

了解上面以后我们就可以知道相同的两个数字按位异或后会变成0，这种异或是符合交换律的。

如： 1 2 3 3 2 1 按位异或后会变成 0 ， 按位异或可以交换数字间的顺序

 那么我们就可以将正常的数组与缺失的数组进行按位异或，最后剩下的数字就是缺失的数字！

int missingNumber(int* nums, int numsSize){
    // 创建按位异或的变量
    int ret = 0;
    for(int i =0; i<numsSize; ++i)
    {
        // 我们可以将i代替为创建的正常数组，但是注意i<numsSize的,说明正常数组缺少最后一个元素
        ret = ret ^ nums[i];
        ret = ret ^ i;
    }

    // 我们要将最后一个元素也按位异或上
        ret ^= numsSize;

        // 返回
        return ret;
}

 2.环形链表

题目信息及链接：141. 环形链表 - 力扣（LeetCode） 

 分析：

题目要求判断是否是环形链表，我们想想可以怎么判断呢？能否以遍历数组看是否能找到尾节点，并且尾节点指向NULL来判断是否是一个环形链表，答案是不可以的，因为环形链表是找不到尾的，它会一直循环，我们是不清楚该循环中什么时候才到尾。 我们需要做到的是判断环形是否存在，那么去判断是否循环两遍同一个节点来判断环形链表是否可行？答案是不行，因为我们不知道该判断哪个节点，该节点是否在环中。

 思路考虑：

既然无法找寻一个合适的判断节点，我们就直接创建一个，我们可以创建快慢指针，快的指针会先进入环内，慢指针后进入环内，如果快指针和慢指针相遇，那么就存在环；如果快指针走到了尾，那么就不存在环形。这样一来我们判断环形链表的问题就转化成了追击问题，但是这又会带来新的问题：

• 快慢指针直接的差距倍数如果是1（慢指针走1步，快指针走2步），那么一定会相遇吗，会不会错过呢？
• 如果差距步数是2，3 ...... N 呢，快慢指针还会相遇吗，会不会错过呢？

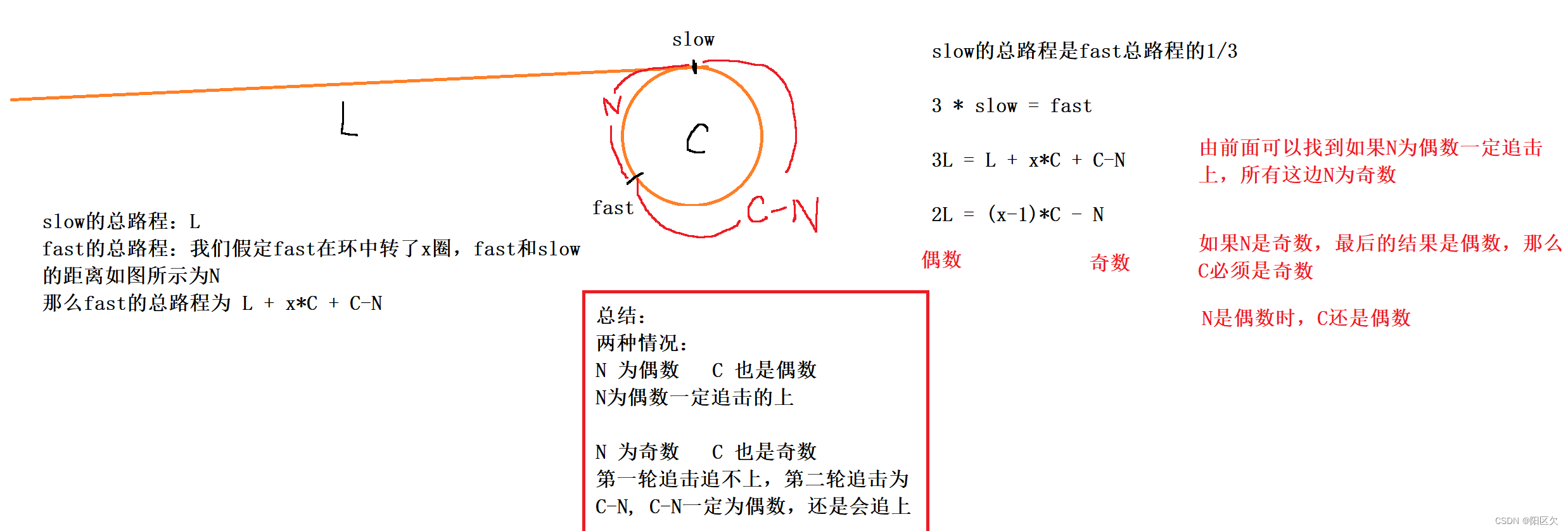
 首先我们假定快指针是慢指针的两倍，那么差距步就是1，设定从头节点到环的距离为L，当slow指针走到一半路程时，快指针刚刚进环。

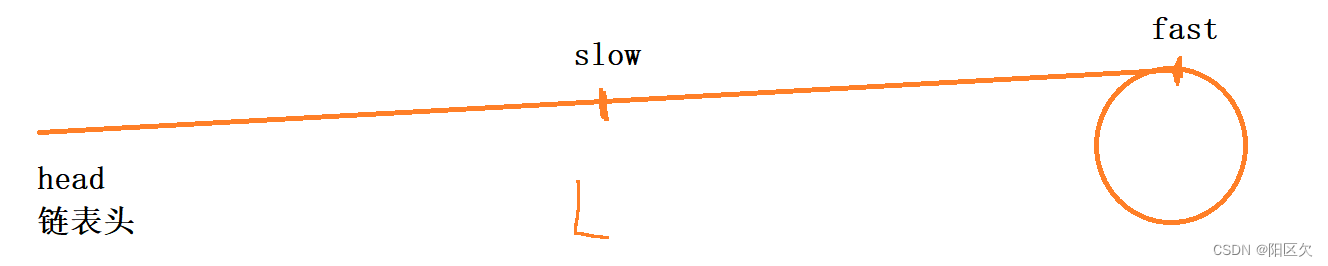当慢指针 刚刚进环，那么快指针已经在环内转了一段距离了，假设现在slow慢指针和fast快指针之间距离差为N,每次差距步为1，那么N, N-1, N-2, N-3，...... 3 ,2, 2 , 0。 最后两个指针一定会相遇！

 然后我们来考虑第二个问题，如果差距步不是1呢，这边就以差距步为2来说明吧，更大还是一样的。

慢指针走1/3，快指针走到进环节点，设定环的长度为C，当慢指针走到进环节点后，快指针已经在环内转了几圈，假设这时慢指针和快指针的距离为N。 如果N是偶数，那么N-2, N-4, N-6, 4, 2, 0 快指针一定能追上慢指针，如果N是奇数，那么N-2, N-4, N-6, 3, 2, -1,快慢指针错过，进行新的一轮追击。

 

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) {
    struct ListNode * fast = head;
    struct ListNode * slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        {
            return true;
        }
    }
    return false;
}

原文地址：https://blog.csdn.net/2301_81577798/article/details/138546666

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！