PyTorch入门之Tensor综合-含操作/运算、机器学习的关系、稠密张量与稀疏张量的定义等
PyTorch入门之Tensor综合-含操作/运算、机器学习的关系、稠密张量与稀疏张量的定义等
Tensor的理解
数学中有标量、向量和矩阵的概念,它们的维度分别是0、1、2。其中:
- 标量可以看成的一个数字,
1,标量中元素的位置固定。 - 向量可以看成是一维表格,向量中元素的位置需要通过其索引确定,表示为

矩阵可以看成是二维表格,矩阵中的元素位置需要通过其行号和列号确定,表示为:

张量(Tensor) 可以视为矩阵的扩展,可以用于表示无穷维度的数据
如果我们用标量、向量或矩阵描述一个事物时,该事物最多可用 [H,W]的维度表示。在现实与客观世界中,我们经常会碰到的物体的维度可能会更高维度,很难通过向量或矩阵来描述,这时我们就需要张量。也就是说,我们可以通过张量来描述任意维度的物体 H * W * C,其中C为C维的特征图(特征图是深度学习中的一个概念),除外我们还可以用Tensor描述更高维度的物体:H * W * C* D,其中D为未知的更高维空间。
总之,张量是对于标量、向量、矩阵之上进行更加泛化的定义。标量可以看成是0阶的张量,向量是1阶段张量,矩阵是2阶的张量,除了0,1,2阶的张量之外,还有3阶、4阶、5阶..n阶的张量。引申到深度学习,其 数据输入的维度是不确定的(可以是任意维度),这时就需要采用一个更加广泛的概念去描述这些量,Tensor就可以更便利解决该问题的。
Tensor的基本概念

其中标量是0维的张量,向量是1维的张量,矩阵是2维的张量。
举例:如下所示,左侧为一个长方体某一切面的矩阵(二阶张量),该矩阵包含N*M个元素,其中每一个元素是一个标量,每一张都是一个向量。一个物体有N个切面,将C 个 N * M 拼接到一起,就会得到一个三阶的张量C*N*M用于表示长方体(如下右图)

在用张量描述物体时,我们需要确定这个张量具体是一个什么样的量,用变量或常量来描述。
Tensor机器学习的关系
完整的机器学习的任务,会涉及到样本、模型等元素(如下所示)。

对于样本(机器学习中用到的数据)我们就可通过Tensor来对其进行描述。比如一条语音数据,我们可有能会采用向量来进行描述,该向量就是1阶的张量。此时向量描述的是语音数据被采样后在当前时刻的声音特征,图形化之后可能为波行。而对于灰度图,我们通常采用矩阵描述(二阶Tensor),表示成H*W,彩色图则会描述成[H * W * C],为一个三阶Tensor,其中C=3。
而模型(模型分为有参数模型与无参数模型),有参数模型一般被描述为 Y = WX + b函数,其中X是指样本,W,B是指参数。当W与B未知的情况下为变量,该变量也是通过Tensor来表示,Y为最后的标签,而标签在进行数字化时也会通过Tensor来对其进行描述。
样本标签与属性关系可描述为
y=f(x),其中x为属性(样本),f为模型。
结论:Tensor可以用来描述机器学习过程中的样本或模型。
Tensor的类型
张量(Tensor)是Pytorch库中的基本数据类型,在 Pytorch中各种基本数字类型都有其对应的Tensor类型(但在Pytorch中没有内嵌的字符串类型)。
类型列表
Tensor的每种类型分别有对应CPU和GPU版本。加粗部分为常用类型。Tensor默认的数据类型FloatTensor。
| - | 数据类型 | torch | CPU Tensor | GPU Tensor |
|---|---|---|---|---|
| 32-bit float point | 32 bit 浮点 | torch.float32 or torch.float | torch.FloatTensor | torch.cuda.FloatTensor |
| 64-bit float point | 64 bit 浮点 | torch.float64 or torch.double | torch.DoubleTensor | torch.cuda.DoubleTensor |
| 16-bit float point | 16 bit 半精度浮点 | torch.float16 or torch.half | torch.HalfTensor | torch.cuda.HalfTensor |
| 8-bit integer(unsigned) | 8 bit 无符号整形(0~255)**** | torch.uint8 | torch.ByteTensor | torch.cuda.ByteTensor |
| 8-bit integer(signed) | 8 bit 有符号整形(-128~127) | torch.int8 | torch.CharTensor | torch.cuda.CharTensor |
| 16-bit integer(signed) | 16 bit 有符号整形 | torch.int16 or torch.short | torch.ShortTensor | torch.cuda.ShortTensor |
| 32-bit integer(signed) | 32 bit 有符号整形 | torch.int32 or torch.int | torch.IntTensor | torch.cuda.IntTensor |
| 64-bit integer(signed) | 64 bit 有符号整形 | torch.int64 or torch.long | torch.LongTensor | torch.cuda LongTensor |
| Boolean | 布尔 | torch.bool | torch.BooleanTensor | torch.cuda.BooleanTensor |
常见类型操作
将普通张量类型转化为GPU张量类型的方法: 普通张量变量名.cuda(), 返回一个GPU张量的引用。
Tensor默认的数据类型
- 默认的Tensor是FloatTensor(如果默认类型为GPU tensor,则所有操作都将在GPU上进行)。
- 设置默认的数据类型:
torch.set_default_tensor_type(类型名) - 增强学习中使用DoubleTensor的使用会更多
- 将张量转换为其他数据类型
- 将张量转换为numpy数组:
张量名.numpy() - 将只有一个元素的张量转换为标量:
张量名.item()。
- 将张量转换为numpy数组:
查看张量数据类型的方法
type方法:使用张量名.type()可以查看张量的具体类型。isinstance:isinstance(torch.randn(2,3),torch.FloatTensor),返回布尔值。
生成元素数据类型指定的张量
浮点型张量
bash复制代码tensor.FloatTensor(标量/列表/numpy数组) # 生成元素均为单精度浮点型的张量
tensor.DoubleTensor(标量/列表/numpy数组) # 生成元素均为双精度浮点型的张量
tensor.HalfTensor(标量/列表/numpy数组) # 生成元素均为半精度浮点型的张量
整型张量
bash复制代码tensor.IntTensor(标量/列表/numpy数组) # 生成元素均为基本整型的张量
tensor.ShortTensor(标量/列表/numpy数组) # 生成元素均为短整型的张量
tensor.LongTensor(标量/列表/numpy数组) # 生成元素均为长整型的张量
布尔型张量
bash
复制代码tensor.BoolTensor(标量/列表/numpy数组) # 生成元素均为布尔类型的张量
Tensor的创建
创建函数
| 函数 | 功能 | 备注 | |
|---|---|---|---|
| Tensor(*size) | 基础构造函数 | size: 直接根据形状定义Tensor, 例:torch.tensor(标量 | 列表), |
| Tensor(data) | 类似np.array | data: 使用数据直接初始化, 例:torch.from_numpy(numpy数组) | |
| ones(*size) | 全1Tensor | 常用结构:全部为1的张量 | |
| zeros(*size) | 全0Tensor | 常用结构:全部为0的常量 | |
| eye(*size) | 对角线为1,其他为0 | 常用结构:对角线为1,其他为0 | |
| arange(s,e,step) | 从s到e,步长为step | 从s到e, 中间的间隔为step,即步长 | |
| linspace(s,e,steps) | 从s到e,均匀切分成steps份 | 从s到e, 均匀切分成steps份 | |
| rand/randn(*size) | 均匀/标准分布 | size: 根据形状定义Tensor, 值为随机赋值,均匀/标准分布的随机采样 | |
| normal(mean,std)/uniform (from,to) | 正态分布/均匀分布 | 满足正态分布或均匀分布的 | |
| randperm(m) | 随机排列 | 对一个序列进行随机排列 | |
| empty(*size) | 生成不经过元素初始化的指定形状的张量 | ||
| rand_like(tensor) | 生成指定填充值的指定形状的张量 | ||
| full(*size) | 指定值的Tensor |
编程实例
python复制代码import numpy as np
import torch
def printTensor(tensor):
print(tensor)
print("numel =", tensor.numel()) # 输出9
print("dim =", tensor.dim()) # 输出2
print("type =", tensor.type()) # 输出2
'''常用的Tensor定义'''
print("--------------as_tensor--------------")
shape = [[2, 3], [4, 5], [6, 7]]
tensor = torch.as_tensor(shape)
printTensor(tensor)
print("--------------Tensor(* Size)--------------")
shape = [(2, 3), (4, 5), [6, 7]]
tensor1 = torch.Tensor(shape)
printTensor(tensor1)
print("--------------numpy.array()--------------")
data_array = np.array([[2, 3], [4, 5], [6, 7]])
tensor = torch.tensor(data_array)
printTensor(tensor)
# 创建一个3行3列的张量
print("--------------torch.ones--------------")
tensor = torch.ones((3, 3))
printTensor(tensor)
print("--------------torch.zeros--------------")
tensor = torch.zeros(2, 2)
printTensor(tensor)
print("--------------torch.zeros_like--------------")
tensorlike = torch.zeros_like(tensor1)
printTensor(tensorlike)
print("--------------torch.randn--------------")
tensor = torch.randn(2, 2)
printTensor(tensor)
'''正态分布'''
print(u"--------------torch.normal mean为均值,std为标准差-1--------------")
# std=5组不同的正诚分布,5组都是随机的标准差和 mean =0
tensor = torch.normal(mean=0.0, std=torch.rand(5))
printTensor(tensor)
print(u"--------------torch.normal mean为均值,std为标准差-2--------------")
# std=5组不同的正诚分布,5组都是随机的标准差和随机的mean
tensor = torch.normal(mean=torch.rand(5), std=torch.rand(5))
printTensor(tensor)
print(u"--------------torch.uniform_--------------")
tensor = torch.Tensor(4, 2).uniform_()
printTensor(tensor)
'''定义一个序列'''
print(u"--------------torch.arange--------------")
# 定义一个序列, 步长为2, 最后10不包含在序列中
tensor = torch.arange(0, 10, 2)
printTensor(tensor)
print(u"--------------torch.linspace--------------")
# 等间节切分,5为个数,11为范围,0为起始值
tensor = torch.linspace(0, 11, 5)
printTensor(tensor)
Tensor的属性
- 每一个Tensor有torch.dtype、torch.device、torch.layout三种属性
- torch.device 标识了torch.Tensor对象在创建之后所存储在的设备名称
- torch.layout表示torch.Tensor内存布局的对象
torch.dtype: 在使用tensor函数创建tensor张量对象时还可以使用dtype参数指定数据类型
torch.device: 张量所创建的数据,到底应该存储在哪个设备上,CPU或GPU, GPU是通过CUDA来表示,多个则用cuda:0, cuda:1,以此类推
torch.layout: 张量的排布方式,对应到内存中连续的区别。稠密或稀疏的方式。
稠密的张量
稠密的张量定义方法
ini复制代码import torch
# GPU
# GPU则代码改为: dev = torch.device("cuda:0")
dev = torch.device("cpu")
a = torch.tensor([1,2,3], dtype=torch.float32,device=dev)
print(a)
稀疏的张量
稀疏或低秩是机器学习中两个很重要的概念,描述了当前数据是否满足某种性质
- 稀疏表达了当前数据中非0元素的个数,非0元素的个数越少,说明越稀疏。如果全部为0则说明最稀疏。
- 低秩描述了数据本身的关联性,也是线性代码中的一个概念。秩从线性相关的角度来看,主要是描述了当前矩阵中的向量间线性可表示的关系。
稀疏的张量在机器学习中的优势
- 从模型角度:能够使模型变的非常简单。对于有参数的模型,如果参数中0的个数非常多,意味着可以对模型进行简化。即参数为0的项(item) 是可以减掉的,因为0乘以任何数都等于0。这样参数个数变少,意味着模型变的更简单,对于参数稀疏化的约束在机器学习中是一个非常重要的性质。这是我们从机器学习模型的角度上介绍稀疏的意义。
- 从数据角度,通过对数据进行稀疏化的表示,可以减少数据在内存中的开销。假设存在一个100*100的矩阵,哪果用稠密方式表示数据,则需要100**100单位的空间,而如果用稀疏张量表示,我们只要记住非0元素的坐标即可。
torch.sparse_coo_tensor
PyTorch中用torch.sparse_coo_tensor 表示稀疏矩阵。使用torch.sparse_coo_tensor可以方便地将稀疏矩阵转换为PyTorch张量,并进行各种操作。同时,由于只存储了非零元素的位置和值,因此可以节省大量的内存空间。
名称是 'coo’代表非零元素的坐标。即coo类型: coo类型表示了非零元素的坐标形式
torch.sparse_coo_tensor参数说明:
- indices: 一个二维的LongTensor, 表示非零元素在原矩阵中的位置,其形状为(N, 2),其中N为非零元素个数。
- values: 一个一维的Tensor, 表示非零元素的值,其形状为(N,)。
- size: 一个元组,表示输出张量的形状,例如(M, N)。
torch.sparse_coo_tensor参数解说:
- indices: 表示非零元素在原矩阵中的位置,即哪些位置是非零的。它的形状为(N, 2), 其中N为非零元素个数。每个元素包含两个值,分别表示该非零元素在行和列上的位置。
- values: 表示非零元素的值,即这些位置上的数值。它的形状为(N,)
- size: 表示输出张量的形状,即输出张量的行数和列数。例如,如果输入矩阵是一个4x5的矩阵,但是只有第2行和第4行、第3列和第5列上的元素是非零的,那么输出张量的形状就是(2, 2)。
torch.sparse_coo_tensor用法
lua复制代码import torch
dev = torch.device("cpu")
# 定义长度分别为3个长度的坐标: [0,2] [1,0] [1,2],
# indices = torch.tensor([[0, 1, 2], [0, 1, 2]]) 会保存数据落地对角线上
indices = torch.tensor([[0, 1, 1], [2, 0, 2]])
# 以上3组从坐标对应的三个非0元素 3,4,5
values = torch.tensor([3, 4, 5], dtype=torch.float32)
# 原张量的形状是一个2,4的tensor, 如果用稠密方式打印,打看到一个2,4的变量
x = torch.sparse_coo_tensor(indices, values, [3, 3], device=dev, dtype=torch.float32)
x_to_dense = x.to_dense()
print("--------sparse_coo_tensor------------")
print(x)
print("--------x_to_dense------------")
print(x_to_dense)
控制台输出

例:将数据落地对角线上
lua复制代码indices = torch.tensor([[0, 1, 2], [0, 1, 2]])
values = torch.tensor([1,2,3], dtype=torch.float32)
Tensor的算术运算
四则运算
- 加减乘除
- 矩阵运算
其他运算
- torch.pow - 幂运算
- torch.exp(input, out=None) - e指数,注意只支持浮点型
- torch.sqrt(input, out=None) - 开方
- torch.log(input, out=None) - 对数运算,以e为底
- ceil/round/floor/trunc - 取整/四舍五入/下取整/只保留整数部分 - 如
torch.ceil(input, out=None) - clamp(input, min, max) - 超过min和max部分截断 -
torch.clamp(input, min, max, out=None) - torch.abs(input, out=None)- 求绝对值
- …
加减法运算
css复制代码import torch
a = torch.rand(2, 3)
b = torch.rand(2, 3)
c = a + b # a - b ,
print(c)
c = torch.add(a, b) # 减法sub
print(c)
print(a.add(b)) # 减法sub,
# a.add_(b) # sub_(...), 带下划线的方式,运算后将结果同时赋给a。加减乘除等运算中含有下划线"_"的规则都一样。
print(a)
减法:- / …sub() / …sub_() 乘法: * /
c = torch.mul(a,b)/a.mul(b)/a.mul_(b)
哈达玛积
哈达玛积(element wise,对应元素相乘) - mul乘法 如果一个tensor是shape是2 * 2 的话,则另外一个tensor也是(2 * 2), 这样保证所有元素都保证每个元素都可以被相乘。
css复制代码c = a * b
c = torch.mul(a, b) # a和b的shape要一样的
a.mul(b)
a.mul_(b) # 同时将结果赋给a
矩阵的乘法
二维矩阵的乘法运算
二维矩阵的乘法运算包括torch.mm(),torch.matmul(),@
规则a * b 时,即两个矩阵相乘,m * n, n * p, 一定要保证 两个矩阵的’n’是相同的。
scss复制代码a = torch.ones(2,1)
b = torch.ones(1,2)
print(torch.mm(a,b))
print(torch.matmul(a,b))
print(a @ b)
print(a.matmul(b))
print(a.mm(b))
高维矩阵的乘法运算
对于高维的Tensor(dim>2),假如矩阵的size=(a1,a2,m,n) ,我们要保证除最后两维m,n之外的前几维的值保持一致, 最后两维的规则同二维矩阵,即n相同 。就像矩阵的索引一样并且运算操只有``torch.matmul()`
同样是除了矩阵内的数值之外,要保证维度的每个元素都可以被计算。
mm()与matmul()不存在下划线类的计算.。
如下所示:n相同,a,b相同。
css复制代码a = torch.ones(a, b, m, n)
b = torch.ones(a, b, n, p)
举例:
css复制代码a = torch.ones(1, 2, 4, 5)
b = torch.ones(1, 2, 5, 3)
print(a.matmul(b))
print(torch.matmul(a, b))
幂运算
scss复制代码a = torch.full((2, 3), fill_value=2)
print(torch.pow(a, 2))
print(a.pow(2))
print(a ** 2)
print(a.pow_(2))
指数运算
函数y=a^x(a>0且a≠1) 叫做指数函数,a是常数,x是自变量,定义域为R,值域为(0,+∞)。要求:a^x前的系数必须是数1,自变量x必须在指数的位置上,且不能是x的其他表达式,否则就不是指数函数。
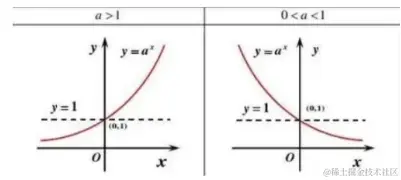
- a>1时,则指数函数单调递增;若0<a<1,则为单调递减的。
- 对于a不大于0的情况,函数的定义域不连续,不考虑; a等于0函数无意义一般也不考虑。
- 指数函数恒过(0,1)点,即水平直线y=1是从递减到递增的一个过渡位置。
- 指数函数是非奇非偶函数。
- …
指数函数应用到自然常数e上写为exp(x),现常写为e^x(表示为x=lny),其图像是单调递增,n∈R,y>0,与y轴相交于(0,1)点。,图像位于X轴上方,第二象限无限接近X轴。
e的x次方
scss复制代码x = torch.full((2, 3), fill_value=2
print(torch.exp(x))
其他(略)
开方运算
lua复制代码a = torch.full((2, 3), fill_value=4)
print(a.sqrt())
# ----返回值-----
tensor([[2., 2., 2.],
[2., 2., 2.]])
对数运算
对数源于指数,是指数函数反函数 因为:N = ax 所以:x = log(aN)
如果 N=a^x(a>0,a≠1),即a的x次方等于N(a>0,且a≠1),那么数x叫做以a为底N的对数(logarithm),记作:x=log(aN) 其中,a叫做对数的底数,N叫做真数,x叫做 “以a为底N的对数”。
scss复制代码a = torch.full((2, 3), fill_value=4)
print(torch.log2(a))
print(torch.log10(a))
print(torch.log(a))
Tensor的更多操作
维度调整
-
查看维度:
torch.shape -
变换维度:
torch.reshape([d0,d1,d2]) -
unsqueeze和
squeezeb=a.squeeze(a)去掉维度值为1的维度b=a.unsqueeze(n)增加一个维度在shape的第n个 c = torch.rand(2, 3) c = c.unsqueeze(1) print(c.shape)
两个tensor合并
markdown复制代码- `torch.cat(tensors, dim=0, out=None)`
- `torch.stack(tensors)`合并时候新建一个维度
与numpy互换
不重复造论子,请看 pytorch和numpy的互转
参考
原文地址:https://blog.csdn.net/weixin_42907150/article/details/135704276
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
