0x00基础算法 -- 0x05 排序

🕗 发布于 2024-11-16 20:52 算法 c++ 数据结构

1、离散化

排序算法的第一个应用：离散化。

“离散化”就是把无穷大（无限）的集合中的若干个（有限）元素映射为有限集合以便于统计的方法。

例如：问题的范围定义在整数集合 $\mathbb{Z}$ ，但是只涉及其中m个有限的数值，并且与数值的绝对大小无关（只把这些数值作为代表，或只与它们的相对顺序有关）-- 我们就可以把整数集合 $\mathbb{Z}$ 中的这m个整数与1~m建立映射关系。如果有一个时间、空间复杂度与数值范围 $\mathbb{Z}$ 的大小有关的算法，在离散化后，该算法的时间、空间复杂度就降低为与m相关。

具体例子：假设问题涉及int范围内的n个整数 a[1]~a[n]，这n个整数可能会有重复，去重后有m个整数，我们把这m个整数a[i] 用一个1~m之间的整数代替，并且保持大小顺序不变，即代替的整数的相对顺序与a[i]的相对顺序一致。

操作方式：排序 + 去重
方式一：
vector<int> alls;
sort(alls.begin(),alls.end()); //排序
alls.erase(unique(alls.begin(),alls.end()),alls.end()); //去重
方式二：
void discrete() //离散化
{
    sort(a + 1, a + n + 1);
    for(int i = 1; i <= n; i++)
    {
        if(i == 1 || a[i] != a[i - 1])
            b[++m] = a[i];
    }
}

int query(int x) //查询x映射为哪个1~m之间的整数
{
    return lower_bound(b + 1, b + m + 1, x) - b; //返回的是地址-b = 下标
}

1.1 题目 -- 电影

103. 电影 - AcWing题库

思路：
根据题意，需要根据语言的种类来进行统计，因为语言的种类靠int数值来区分，所以最直接的做法就是，直接利用语言种类的int数值来作为下标，但语言最多涉及2*m+n种，远远小于int的最大值，所以可以通过离散化将稀疏下标变成稠密下标，用1~2*m + n之间的整数来代替每种语言。这样我们就可以用数组直接统计会上述每种语言的人的数量，从而选择满足题目要求的电影。时间复杂度为O((n + m)log(n + m)).

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

vector<int> a,b,c,alls;

int find(int x) //查找离散后的结果,alls中的下标
{
    //二分法
    int l = 0, r = alls.size() - 1;
    while(l < r)
    {
        int mid = (l + r) >> 1;
        if(alls[mid] >= x)
            r = mid;
        else
            l = mid + 1;
    }
    return r;
}

int main()
{
    int n,m,tmp;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> tmp;
        a.push_back(tmp);
        alls.push_back(tmp);
    }
    cin >> m;
    for(int i = 0; i < m; i++)
    {
        cin >> tmp;
        b.push_back(tmp);
        alls.push_back(tmp);
    }
    for(int i = 0; i < m; i++)
    {
        cin >> tmp;
        c.push_back(tmp);
        alls.push_back(tmp);
    }
    
    //排序+去重
    sort(alls.begin(),alls.end());
    alls.erase(unique(alls.begin(),alls.end()),alls.end());
    
    vector<int> res(alls.size(),0);
    for(int i = 0; i < a.size(); i++)
    {
        res[find(a[i])]++;
    }
    int ans_1 = 0, ans_2 = 0, ans_index = 0;
    for(int i = 0; i < m; i++)
    {
        int ans_x = res[find(b[i])], ans_y = res[find(c[i])];
        if(ans_x > ans_1 || (ans_x == ans_1 && ans_y > ans_2))
            ans_index = i, ans_1 = ans_x, ans_2 = ans_y;
    }
    cout << ans_index + 1 << endl; //+1是因为题目下标从1开始
    return 0;
}

2、中位数

先通过例题了解中位数的题型

2.1 题目 -- 货舱选址

104. 货仓选址 - AcWing题库

思路：
先来看一个简单的例子，假如有两个商店的情况：

可以发现在x1~x2中任选一点（包括x1和x2），路径总和最小，此时可以认为x1或x2是x1、x2中的中位数。

假如有三个商店的情况：

可以发现选择x2时总路径和最短，此时x2是x1、x2、x3的中位数。

根据上面的两种情况，可以推广到任意奇数个商店和任意偶数个商店，同样是取中位数时总距离之和最小。
把A[1]~A[N]排序，设货仓建在X坐标处，X左侧的商家有P家，右侧的商店有Q家；
若P < Q，则每次把货仓向右移动1单位距离，距离之和就会变小Q-P（根据上面的xi和yi一组的方式可以简单证明，以商店为偶数个为例，如果P < Q，那么就一定有P个组满足xi和yi为一组，即x在xi~yi内距离都为yi - xi，对于其他Q-P个组，不满足该性质，且每次向右移动，每个商店到货仓的距离都-1，所以距离之和会变小Q-P）。

若P > Q，则每次把货仓向左移动1单位距离，距离之和就会变小P-Q。

当P=Q时为最优解。(即取中位数时)
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
using LL = long long;

const int N = 100010;
int A[N];
int n;

int main()
{
    cin >> n;
    for(int i = 0; i < n; i++)
        cin >> A[i];
    sort(A, A + n);
    LL res = 0;
    for(int i = 0; i < n; i++)
    {
        res += abs(A[i] - A[n / 2]);
    }
    cout << res << endl;
    
    return 0;
}

2.2 经典问题 -- "均分纸牌"和"环形均分纸牌"

"均分纸牌"：有M个人排成一行，每个人手中分别有 C[ 1 ] ~ C[ M ] 张纸牌，在每一步操作中，可以让某个人把自己手中的一张纸牌交给他旁边的一个人（每一步只能交给相邻的人），求至少需要多少步操作才能让每个人手中持有的纸牌数相等。

思路：

最终结果是每个人手中的纸牌数相等，假设一共有T张牌，M个人，那么一定要使T/M整除才会有最终每个人手中的纸牌数相等。
先考虑第一个人：
若C[1]>T/M，则第一个人需要给第二个人 C[1] - T/M 张纸牌，即把C[2]加上C[1]-T/M；
若C[1]<T/M，则第一个人需要从第二个人手中取T/M-C[1]张纸牌，即把C[2]减去T/M-C[1]；
推广到后面的第2~M个人：
按照第2步的方式依次考虑第2~M个人，由于牌的总数在操作中不会改变，所以即使某个时刻有某个C[i]被减为负数也没有关系，因为接下来C[i]会从C[i+1]处拿牌...（实际过程中C[i]先从C[i+1]取牌，再C[i - 1]从C[i]中取牌；但该算法与具体过程无关，所以可以按照C[i]到C[i+1]的顺序进行）直到C[M]，如果T/M能整除，一定会有C[M] = T/M。
最小步数公式： $\sum_{i=2}^{M}(|C[i] - C[i-1]|),C[i] \pm |C[i]-C[i-1]|$ ，缺点需要动态更新C[i]
最小步数公式优化：因为每次操作都是相邻位置，达到目标所需要的最小步数： $\sum_{i= 1}^{M}|i*\frac{T}{M}-G[i]|$ ，其中G是C的前缀和，即 $G[i] = \sum_{j = 1}^{i} C[j]$ ；含义：每个前缀和并表示最初共持有G[i]张牌，最终会持有 i*T/M，多退少补，会与后边的人发生"二者之差的绝对值"张纸牌的交换；优点：先处理前缀和，后面直接求值，无需动态更新。
思路转换：如果设A[i] = C[i] - T/M，即一开始就让每个人手中的纸牌都减去T/M，并且最终每个人手中都恰好有0张牌，显然最小操作步数仍然不变： $\sum_{i=1}^{M}|S[i]|$ ，其中S是A的前缀和， $S[i]=\sum_{j=1}^{i}A[j]$ 。

可以发现上面的纸牌传递是一个"单链"的结构，从1开始M结束；如果加上"第1个人和第M个人也是相邻的"，问题就转化成"环形均分纸牌问题"，仔细思考可以发现，一定存在一种最优解的方案，环上某两个相邻的人之间没有发生纸牌交换操作，这就转化成了一般的"纸牌均分问题"。于是可以通过枚举这个没有发生纸牌交换操作的位置，把环断开看成一行转化成一般的"纸牌均分"进行计算。

为什么"环形均分纸牌"能拆环成链？
成环至少需要三个点，先看三个点的情况：通过三个点的情况，由数学归纳法可以推广到任意个数的情况，都可以将整体划成三个部分，其中avg = T / 3（只划分成3个部分），根据上面3个点的基础情况可证：一定存在一种最优的方案，环上某两个相邻的人之间没有发生纸牌交换操作。
拆环成链后的操作：
结合上面已经分析的"均分纸牌"问题，一般均分纸牌问题相当于是在第M个人与第1个人之间把环断开，此时这M个人写成一行，其持有的纸牌数、前缀和分别是：

如果在第k个人之后把环断开写成一行，这M个人持有的纸牌数、前缀和分别是：

此处A是减去T/M后的数组，A数组均分后没人手上0张纸牌，所以有S[M] = 0，也就是说，从第k个人把环断开写成一行，前缀和数组的变化是每个位置都减掉S[K]。
根据上面的推导，可以得到最少步数为： $\sum_{i=1}^{M}|S[i]-S[k]|$ ，其中S是A的前缀和，即 $\sum_{j=1}^{i}A[j]$ ，在该最小步数公式中，k是定值，问题可以进一步转化为"k取何值时上式最小"，可以通过上面的"货仓选址"，也就是中位数算法解决！！！

所以利用中位数算法，根本不需要枚举k，也就是不用枚举没有交换的位置；直接对S[i]排序，求出中位数作为S[K]即为最优解，时间复杂度O(N log N + M log M)。

2.3 题目 -- 七夕祭

105. 七夕祭 - AcWing题库

思路：
解法一："均分纸牌"

可以发现交换左右相邻两个或上下相邻两个摊位：
同一行中，交换左右相邻两个摊点只会改变某两列中cl感兴趣的摊点的数量，不会改变每一行中cl感兴趣的摊点的数量。
同理，同一列中，交换上下相邻两个摊点只会改变某两行中cl感兴趣的摊点的数量，不会改变每一列cl感兴趣的摊点的数量。
总结，cl感兴趣的摊点的数量在行和列变化时，行和列的变化相互之间不会产生影响，这代表我们可以将行和列互相独立开进行计算。
通过最少次数的左右交换使每列中cl感兴趣的摊点数相同
通过最少次数的上下交换使每行中cl感兴趣的摊点数相同
由于第2点讨论的两种情况实际上是一样的，我们可以只分析一种，例如使每一列cl感兴趣的摊点数相同：
记每一列cl感兴趣的摊点数为：C[1]~C[M]，若cl感兴趣的摊点数总数T不能被M整除，则不可能达到要求；若T能被M整除，则说明可以平分，让每一列中有T/M个cl感兴趣的摊点数。
这就可以转化为上面"均分纸牌"的问题了，整个问题就是对行和列两次使用"均分纸牌"，最后将行和列分别求出的最小操作数求和，就是题目整体的答案。

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long LL;

const int N = 1e5 + 10;
int n,m,t;
int row[N]; //存储每一行中持有纸牌的数量--cl感兴趣的摊位数
int col[N]; //存储每一列中持有纸牌的数量--cl感兴趣的摊位数
LL sum[N]; //前缀和数组
bool is_row,is_col; //判断行列是否能平分
LL res; //操作数

int main()
{
    cin >> n >> m >> t;
    int r,c;
    for(int i = 1; i <= t; i++)
    {
        cin >> r >> c;
        row[r]++,col[c]++;
    }
    //使每一行中cl感兴趣的摊位数一致--使每一行中持有的纸牌数一致
    if(!(t % n))
    {
        is_row = true;
        //处理前缀和
        for(int i = 1; i <= n; i++)
        {
            row[i] -= int(t/n); //减去平均值，最后均分时每人手上0张牌
            sum[i] = sum[i - 1] + row[i];
        }
        //排序，求中位数
        sort(sum + 1, sum + 1 + n);
        int mid = n / 2 + 1;
        //求最小操作数
        for(int i = 1; i <= n; i++)
            res += abs(sum[i]-sum[mid]);
    }
    
    //使每一列中cl感兴趣的摊位数一致--使每一列中持有的纸牌数一致
    if(!(t % m))
    {
        is_col = true;
        //处理前缀和
        for(int i = 1; i <= m; i++)
        {
            col[i] -= int(t/m);
            sum[i] = sum[i - 1] + col[i];
        }
        sort(sum + 1, sum + 1 + m);
        int mid = m / 2 + 1;
        for(int i = 1; i <= m; i++)
            res += abs(sum[i]-sum[mid]);
    }
    
    //处理输出
    if(is_col && is_row)
        cout << "both" << ' ' << res;
    else if(is_col)
        cout << "column" << ' ' << res;
    else if(is_row)
        cout << "row" << ' ' << res;
    else
        cout << "impossible";
    
    return 0;
}

解法二：公式推导

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;

const int N = 1e5 + 10;
int row[N],col[N];
LL sum[N],c[N];
int n,m,t;

LL calc(int n, int* a)
{
    if(t % n != 0)
        return -1;
    //前缀和
    for(int i = 1; i <= n; i++)
        sum[i] = sum[i-1] + a[i];
        
    int avg = t / n;
    c[1] = 0;
    for(int i = 2; i <= n; i++)
        c[i] = sum[i-1] - (i - 1)*avg;
        
    //排序，取中位数
    sort(c + 1, c + 1 + n);
    LL res = 0;
    //x1是c[i]中的中位数 = c[(n+1)/2]
    for(int i = 1; i <= n; i++)
        res += abs(c[i] - c[(n+1)/2]);
    return res;
}

int main()
{
    cin >> n >> m >> t;
    for(int i = 1; i <= t; i++)
    {
        int r,c;
        cin >> r >> c;
        row[r]++,col[c]++;
    }
    
    LL r = calc(n,row);
    LL c = calc(m,col);
    
    if(r != -1 && c != -1)
        cout << "both" << ' ' << r + c;
    else if(r != -1)
        cout << "row" << ' ' << r;
    else if(c != -1)
        cout << "column" << ' ' << c;
    else
        cout << "impossible";
    
    return 0;
}#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;

const int N = 1e5 + 10;
int row[N],col[N];
LL sum[N],c[N];
int n,m,t;

LL calc(int n, int* a)
{
    if(t % n != 0)
        return -1;
    //前缀和
    for(int i = 1; i <= n; i++)
        sum[i] = sum[i-1] + a[i];
        
    int avg = t / n;
    c[1] = 0;
    for(int i = 2; i <= n; i++)
        c[i] = sum[i-1] - (i - 1)*avg;
        
    //排序，取中位数
    sort(c + 1, c + 1 + n);
    LL res = 0;
    //x1是c[i]中的中位数 = c[(n+1)/2]
    for(int i = 1; i <= n; i++)
        res += abs(c[i] - c[(n+1)/2]);
    return res;
}

int main()
{
    cin >> n >> m >> t;
    for(int i = 1; i <= t; i++)
    {
        int r,c;
        cin >> r >> c;
        row[r]++,col[c]++;
    }
    
    LL r = calc(n,row);
    LL c = calc(m,col);
    
    if(r != -1 && c != -1)
        cout << "both" << ' ' << r + c;
    else if(r != -1)
        cout << "row" << ' ' << r;
    else if(c != -1)
        cout << "column" << ' ' << c;
    else
        cout << "impossible";
    
    return 0;
}

2.4 题目 -- 动态中位数 -- "对顶堆"做法

106. 动态中位数 - AcWing题库

思路：
使用做法“对顶堆”：

建立两个二叉堆，一个小根堆、一个大根堆。依次读入这个整数序列的过程中，设当前序列长度为M，需要始终保持规则：

序列中从小到大排名为1 ~ M/2的整数存储在大根堆中
序列中从大到小排名为M/2 + 1 ~ M的整数存储在小根堆中
由上面两个规则可以得出结论：小根堆的元素个数 >= 大根堆的元素个数，且差值不超过1。

任何时候，如果某一个堆中元素个数过多，打破了上述规则，就取出该堆的堆顶插入到另一个堆，始终保持上述规则，当M为奇数时，小根堆的堆顶就是当前序列中的中位数。

每次新读入一个数值x后，若x比中位数小，则插入大根堆；若x比中位数大，则插入小根堆；插入后需要检查并维护上述规则。
#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;

int main()
{
    int t,n,m;
    scanf("%d",&t);
    while(t--)
    {
        priority_queue<int> q;//q为大根堆
        priority_queue<int,vector<int>,greater<int>> p;//p为小根堆
        scanf("%d %d",&n,&m);
        cout<<n<<' '<<(m+1)/2<<endl;
        int cnt=0;
        for(int i=1;i<=m;i++)
        {
            scanf("%d",&n);
            p.push(n);
            if(q.size()&&q.top()>p.top())
            {
               int a=p.top(),b=q.top();
               p.pop(),q.pop();
               p.push(b),q.push(a);
            }
            if(p.size()>q.size()+1)
            {
                q.push(p.top());
                p.pop();
            }
             if(i&1)//奇数
                printf("%d%c",p.top(),++cnt%10==0 ? '\n':' ');//每10个数换一行
        }
        if(cnt%10) cout<<endl;
    }
    return 0;
}

3、第k大数

给定n个整数，求第k大的数：

快排思想：从大到小快速排序：在每一层递归中，随机选取一个数为基准值，把比基准值大的交换到“左半段”，把比基准值小的交换到“右半段”，然后继续递归对左右半段分别进行排序（把基准值自身和其右边的数作为“右半段”），在平均情况下时间复杂度为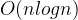 $O(n log n)$

方法一：直接这n个整数进行快排，然后输出从大到小排在第k个的数，时间复杂度为 $O(n log n)$ ；这属于对全部数据快排后的做法。

方式二：利用快排的思想，在每次选取基准值后，统计出大于基准值的数的数量cnt，如果k<=cnt，我们就在左半段（比基准值大的数中）寻找第k大数（只继续递归左半段，右半段无需再递归）；如果k>cnt，我们就在右半段（比基准值小的数中）寻找第k-cnt大数（同理，只递归右半段）...直到区间只剩一个值，即为第k大数。
寻找第k大数时，我们只需要进入左右半段二者之一继续递归，在平均情况下，复杂度为n + n/2 + n/3 + ... + 1 = O(n)。

4、利用归排思想求逆序对

对于一个序列a，若 i < j 且 a[i] > a[j]，则称a[i]与a[j]构成逆序对。
朴素求逆序对：下标 i 从前开始遍历，判断当前 i 位置的值后续是否有小于该位置的值，小于该值即可构成逆序对。

归并求逆序对：
利用归并排序可以在O(n log n)的时间里求出一个长度为n的序列中逆序对的个数。
递归对左右两半排序时，可以把左右两半各自内部的逆序对数作为子问题计算，因此只需要在合并时考虑"左边一半里一个较大的数"与"右边一半里一个较小的数"构成逆序对的情形，求出这种情形的个数。（统计逆序对在合并时统计）

合并时求逆序对的策略：

合并两个有序序列a[l~mid]和a[mid+1~r] 可以采用两个指针 i 和 j 分别对这两个区间进行扫描，不断比较两个指针所指向数值 a[i] 和 a[j] 的大小，将小的值加入到排序的结果数组中。
若小的值是 a[i]，直接假如到结果数组中；
若小的值是 a[j]，则 a[i~mid]都比 a[j] 要大，a[i~mid]这mid - i + 1个值都会与 a[j]构成逆序对，可以顺便统计到逆序对总数的答案中。
void merge(int l, int mid, int r)
{
    //上面是递归操作--先忽略
    //下面是合并操作
    //合并a[l~mid]与a[mid+1,r]
    //a是待排序数组，b是临时数组存着排序结果，cnt表示逆序对个数
    int i = l, j = mid + 1;
    for(int k = l; k <= r; k++)
        if(j > r || i <= mid && a[i] <= a[j])
            b[k] = a[i++];
        else
            b[k] = a[j++], cnt += mid - i + 1;
    //拷贝回去
    for(int k = l; k <= r; k++)
        a[k] = b[k];
}

4.1 题目 -- 超快速排序

107. 超快速排序 - AcWing题库

思路：通过比较和交换相邻两个数值的排序方法，实际上就是冒泡排序，排序过程中交换一次一对大小颠倒的相邻数值，就会使整个序列的逆序对个数减少1，最终排好序后逆序对个数为0，所以对a进行冒泡排序需要的最少交换次数就是序列a中逆序对的个数。求逆序对个数可以直接用归并排序来求出逆序对个数，即为最小交换操作数。
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 5e5 + 10;
int a[N],b[N];
int n;
long long res;//逆序对个数

void merge(int l,int r)
{
    //递归操作
    if(l >= r)
        return;
    int mid = (l+r-1) >> 1;
    merge(l,mid);
    merge(mid + 1,r);
    //合并操作
    int i = l,j = mid + 1;
    for(int k = l; k <= r; k++)
        if(j > r || (i <= mid && a[i] <= a[j]))
            b[k] = a[i++];
        else
            b[k] = a[j++],res += mid - i + 1;
    
    //拷贝回去
    for(int k = l; k <= r; k++)
        a[k] = b[k];
}

int main()
{
    while(cin >> n,n)
    {
        res = 0;
        for(int i = 1; i <= n; i++)
            cin >> a[i];
        merge(1,n);
        cout << res << endl;
    }
    
    return 0;
}

4.2 题目 -- 奇数码问题

108. 奇数码问题 - AcWing题库

思路：
两个局面可达，当且仅当两个局面下网格中的数依次写成一行n*n-1个元素的序列后（不考虑空格），逆序对个数的奇偶性相同。空格左右移动时，写成的序列显然不变；空格向上(下)移动时，相当于某个数与它后(前)边的n-1个数交换了位置，因为n-1是偶数，所以逆序对数的变化也还是偶数。

#include <cstdio>
#include <iostream>

const int MAXN = 500 * 500 + 5;
int arr[MAXN], brr[MAXN], b[MAXN];

long long cnt = 0;
void mergeSort(int a[MAXN], int l, int mid, int r) 
{
    int i = l, j = mid + 1;
    for (int k = l; k <= r; k++) 
    {
        if(j > r || i <= mid && a[i] <= a[j]) 
            b[k] = a[i++];
        else 
            b[k] = a[j++], cnt += mid - i + 1;
    } 
    for (int k = l; k <= r; k++) 
        a[k] = b[k];
}

void merge(int l, int r, int a[MAXN]) 
{
    if(l < r) 
    {
        int mid = (l + r) >> 1;
        merge(l, mid, a);
        merge(mid + 1, r, a);
        mergeSort(a, l, mid, r);
    }
}

int main() 
{
    int n;
    while(scanf("%d", &n) != EOF) 
    { //多组数据的输入方式
        int kx = 0, ky = 0;
        for (int i = 1; i <= n * n; i++) 
        {
            int x = 0;
            scanf("%d", &x);
            if(x != 0) arr[++kx] = x;
        }
        for (int i = 1; i <= n * n; i++) 
        {
            int x = 0;
            scanf("%d", &x);
            if(x != 0) brr[++ky] = x;
        }

        if(n == 1) { puts("TAK"); continue; }

        long long ans_arr = 0, ans_brr = 0;
        merge(1, kx, arr);
        ans_arr = cnt, cnt = 0;
        merge(1, ky, brr);
        ans_brr = cnt, cnt = 0;

        if((ans_arr & 1) != (ans_brr & 1)) puts("NIE");
        else if(std::abs(ans_brr - ans_arr) % 2 == 0) puts("TAK");
        else puts("NIE");
    } return 0;
}

原文地址：https://blog.csdn.net/cookies_s_/article/details/143753064

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！

上一篇：openai 论文Scaling Laws for Neural Language Models学习
下一篇：Vue 3 条件渲染与列表渲染完整指南

docker安装minio、使用springboot集成minio同时创建并设置minio桶仅可读
其中请自行修改用户名、密码、挂载目录和对应的端口与映射（密码至少需要9位，否则启动报错）其中9001是后台服务的端口。
阅读更多2024-11-16
『VUE』27. 透传属性与inheritAttrs（详细图文注释）
『VUE』27. 透传属性与inheritAttrs（详细图文注释）
阅读更多2024-11-16
PostgreSQL物化视图详解
随着数据库规模的增大和查询复杂性的提高，数据库查询的性能问题变得越来越突出。为了优化查询性能，数据库系统引入了物化视图的概念。物化视图是一种预先计算和存储的查询结果，它可以在需要时直接提供查询结果，而
阅读更多2024-11-16
每日一题之进制转换
对于给定的十进制整数N（N<100000），将1到N（含N）之间的每个整数转成十六进制，求转换后的所有十六进制数中含A的总个数。提示：某个数的16进制含A的个数可以参照下面的例子：对于整数42
阅读更多2024-11-16
web与网络编程
通常使用的网络(包括互联网)都是在TCP/IP协议族的基础上运作的。而HTTP属于它内部的一个。
阅读更多2024-11-16
塑料薄膜厂需要用到哪些自动化备件
此外，根据塑料薄膜厂的具体需求和规模，还可能需要其他特定的自动化备件，如自动化流水线、全自动分切机、自动测试机等。在选择备件时，塑料薄膜厂应优先考虑备件的质量、耐用性、兼容性和售后服务等因素，以确保备
阅读更多2024-11-16
实验二：Docker存储配置与管理
非持久化数据是不需要保存的那些数据，容器本地存储中的数据就属于这种类型。容器创建时会创建非持久化存储，这是容器全部文件和文件系统保存的地方。默认情况下，在容器内创建的所有文件都存储在可写容器层，文件系
阅读更多2024-11-16
git本地分支推送到远程和远程pull到本地
在推送到远程仓库之前，你也可能想要先执行 git fetch 和 git pull 以确保你的本地分支是最新的。要将本地分支推送到远程仓库的某个分支（可以是同名的分支，也可以是不同名的分支），你可以使
阅读更多2024-11-16
大模型时代，呼叫中心的呼入机器人系统如何建设？
作者：开源呼叫中心系统 FreeIPCC，Github地址：https://github.com/lihaiya/freeipcc呼叫中心呼入机器人系统的建设是一个涉及多个环节和领域的综合性工程。
阅读更多2024-11-16
HTTP/2新型DDoS攻击：技术深度剖析与防御指南
在智能化演进和互联网技术高速发展的背景下，黑客攻击手段不断翻新，DDoS攻击的强度、频率和复杂度也随之持续攀升。金融、政务、互联网等多个领域及其关键基础设施正面临着前所未有的DDoS攻击威胁。
阅读更多2024-11-16