哈夫曼树(Huffman Tree)
哈夫曼树是一种特殊的二叉树,它是由美国计算机科学家David A.Huffman于1952年提出的。哈夫曼树广泛应用于数据压缩、编码等领域,因为它可以有效地减少数据的存储空间和传输时间。
一、预备知识:
1.结点的权:有某种现实含义的数值(如:表示结点的重要性等)
2.结点的带权路径长度:从树的根到该结点的路径长度(经过的边数〉与该结点上权值的乘积
3.树的带权路径长度:树中所有叶结点的带权路径长度之和(WPL, Weighted Path Length)
来看几个例子:
EX1: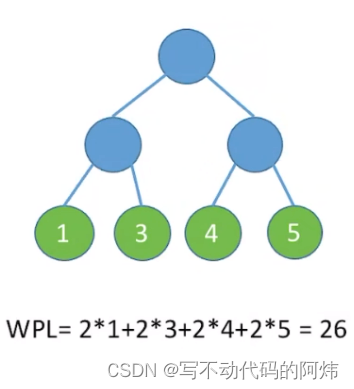 EX2:
EX2: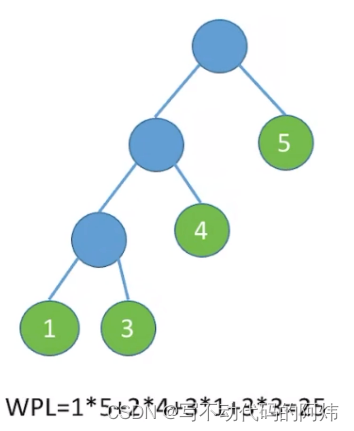
EX3: EX4:
EX4: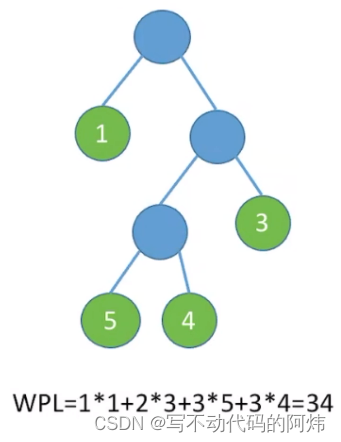
在含有n个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树.
二、哈夫曼树的构造:
给定n个权值分别为w,, w2..., w,的结点,构造哈夫曼树的算法描述如下:
1)将这n个结点分别作为n棵仅含一个结点的二叉树,构成森林F。
2)构造一个新结点,从F中选取两棵根结点权值最小的树作为新结点的左、右子树
并且将新结点的权值置为左、右子树上根结点的权值之和。
3)从F中删除刚才选出的两棵树,同时将新得到的树加入F中。
4)重复步骤2)和3),直至F中只剩下一棵树为止。
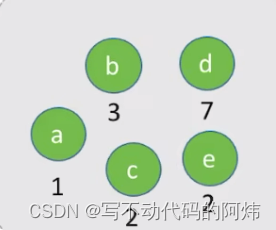
step1: 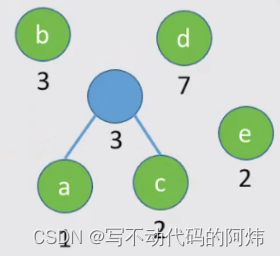
step2: 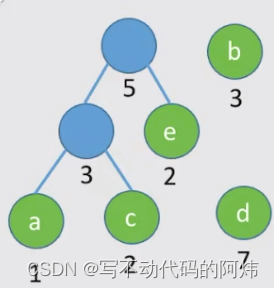
step3: 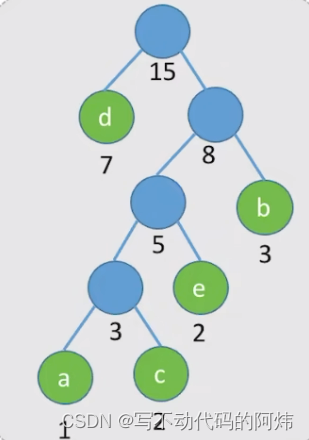
tips:
1)每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大
2)哈夫曼树的结点总数为2n -1
3)哈夫曼树中不存在度为1的结点。
4)哈夫曼树并不唯一,但WPL必然相同且为最优
还可以如下构造:
step1: 
step2: 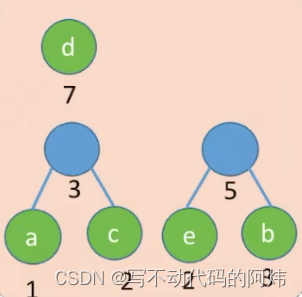
step3: 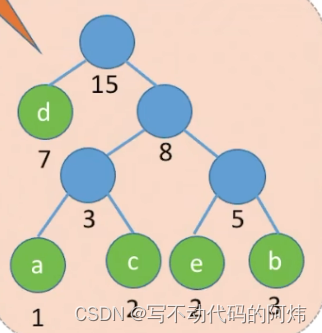
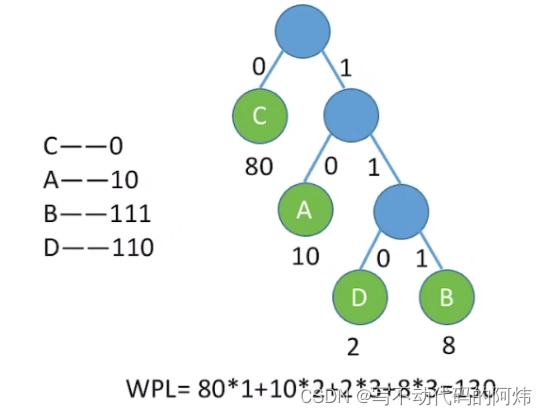
三、哈夫曼编码:
哈夫曼编码是一种用于数据压缩的算法,它通过将频繁出现的字符用较短的二进制码表示,而将较少出现的字符用较长的二进制码表示,从而实现数据的压缩。
固定长度编码――每个字符用相等长度的二进制位表示
可变长度编码――允许对不同字符用不等长的二进制位表示
若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码
有哈夫曼树得到哈夫曼编码――字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点的权值,根据之前介绍的方法构造哈夫曼树
相关代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct Node {
char data; // 字符
int weight; // 权值
struct Node *left, *right; // 左右子节点
} Node;
// 创建新节点
Node* createNode(char data, int weight) {
Node *node = (Node *)malloc(sizeof(Node));
node->data = data;
node->weight = weight;
node->left = node->right = NULL;
return node;
}
// 构建哈夫曼树
Node* buildHuffmanTree(char *data, int *weight, int size) {
Node **nodes = (Node **)malloc(size * sizeof(Node *));
for (int i = 0; i < size; i++) {
nodes[i] = createNode(data[i], weight[i]);
}
while (size > 1) {
int min1 = -1, min2 = -1;
for (int i = 0; i < size; i++) {
if (min1 == -1 || nodes[i]->weight < nodes[min1]->weight) {
min2 = min1;
min1 = i;
} else if (min2 == -1 || nodes[i]->weight < nodes[min2]->weight) {
min2 = i;
}
}
Node *newNode = createNode('\0', nodes[min1]->weight + nodes[min2]->weight);
newNode->left = nodes[min1];
newNode->right = nodes[min2];
nodes[min1] = newNode;
nodes[min2] = nodes[size - 1];
size--;
}
return nodes[0];
}
// 生成哈夫曼编码
void generateHuffmanCode(Node *root, char *code, int depth) {
if (root == NULL) {
return;
}
if (root->left == NULL && root->right == NULL) {
printf("%c: %s
", root->data, code);
}
char leftCode[100], rightCode[100];
strcpy(leftCode, code);
strcat(leftCode, "0");
strcpy(rightCode, code);
strcat(rightCode, "1");
generateHuffmanCode(root->left, leftCode, depth + 1);
generateHuffmanCode(root->right, rightCode, depth + 1);
}
// 解码哈夫曼编码
void decodeHuffmanCode(Node *root, char *code) {
Node *cur = root;
while (*code != '\0') {
if (*code == '0') {
cur = cur->left;
} else {
cur = cur->right;
}
if (cur->left == NULL && cur->right == NULL) {
printf("%c", cur->data);
cur = root;
}
code++;
}
printf("
");
}
int main() {
char data[] = {'A', 'B', 'C', 'D'};
int weight[] = {8, 3, 3, 6};
int size = sizeof(data) / sizeof(data[0]);
Node *root = buildHuffmanTree(data, weight, size);
printf("Huffman Code:
");
generateHuffmanCode(root, "", 0);
printf("Decode: ");
decodeHuffmanCode(root, "1001011"); // 输出:ABCD
return 0;
}
原文地址:https://blog.csdn.net/m0_64055811/article/details/137967524
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
