二叉树_堆（下卷）

前言

接前面两篇的内容，接着往下讲二叉树_堆相关的内容。

正文

那么，回到冒泡排序与堆排序的比较。

我们知道冒泡排序的时间复杂度为$O(N^2)$，这个效率是不太好的。

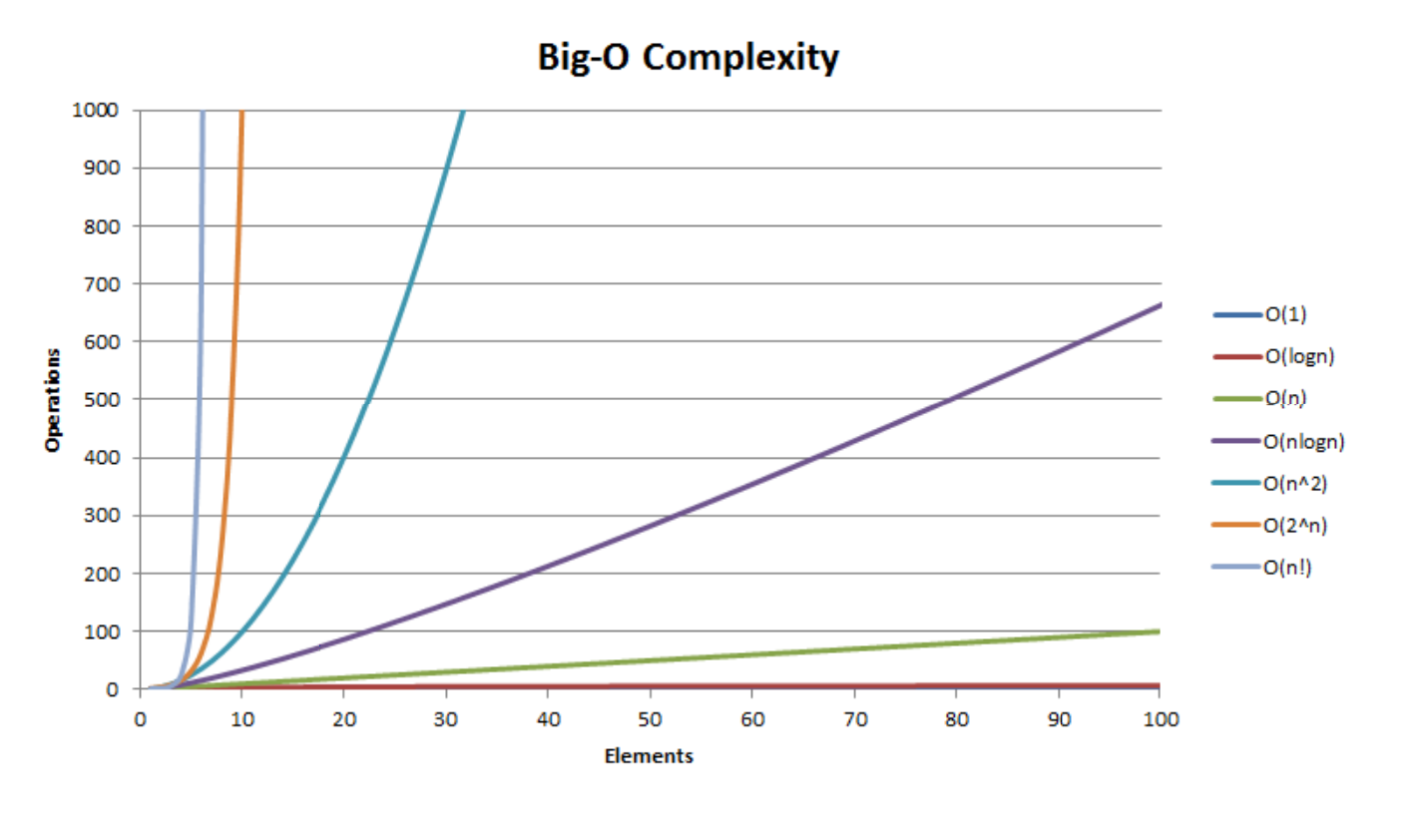
那么，我们的堆排序的时间复杂度如何呢？

由于堆排序中我们使用到向下和向上调整，所以我们要先看看这两个算法的时间复杂度。

我们先看向上调整，主要看的是最多循环次数，如果我们的二叉树有k层，最大结点数为n，我们已经知道根据二叉树的性质：$2^k-1=n$; $k=lo{g}_2(n+1)$。

我们的向上调整的最差情况是和层次有关的。所以最后我们的向上调整算法的时间复杂度就为$O(logn)$。

而在这里我们循环n次向上调整，所以堆排序中建堆这一步的时间复杂度为$O(nlogn)$。

我们再看后面这一步的时间复杂度。很明显，我们得看向下调整的时间复杂度。

因为向下调整也是和层次有关，我们可以粗估时间复杂度也为$O(logn)$。

那么最后我们的堆排序的时间复杂度为$O(nlogn)$+$O(logn)$，因为取的是对结果影响最大的那个，所以堆排序最后我们粗估的时间复杂度就为$O(nlogn)$。

建堆的时间复杂度到底是不是$O(nlogn)$，有待考证。

可以看看上面不同复杂度对比的图，发现冒泡排序的效率是比堆排序差很多的。

但是，我们仔细分析一下向上调整的时间复杂度，发现并不是我们刚才说的这么简单，因为我们的n在变化的过程中，需要交换的次数也是变化的。

在具体分析向上调整算法建堆的时间复杂度之前，我们先来说一个东西：这个是我们的向上调整算法建堆，其实我们还可以由向下调整方法来建堆。

---

向下调整算法建堆

（以大堆为例）

我们还是从堆顶也就是数组最前面的数据开始调整，要将堆顶的数据向下调整意味着下面的数据必须是有效的大堆。

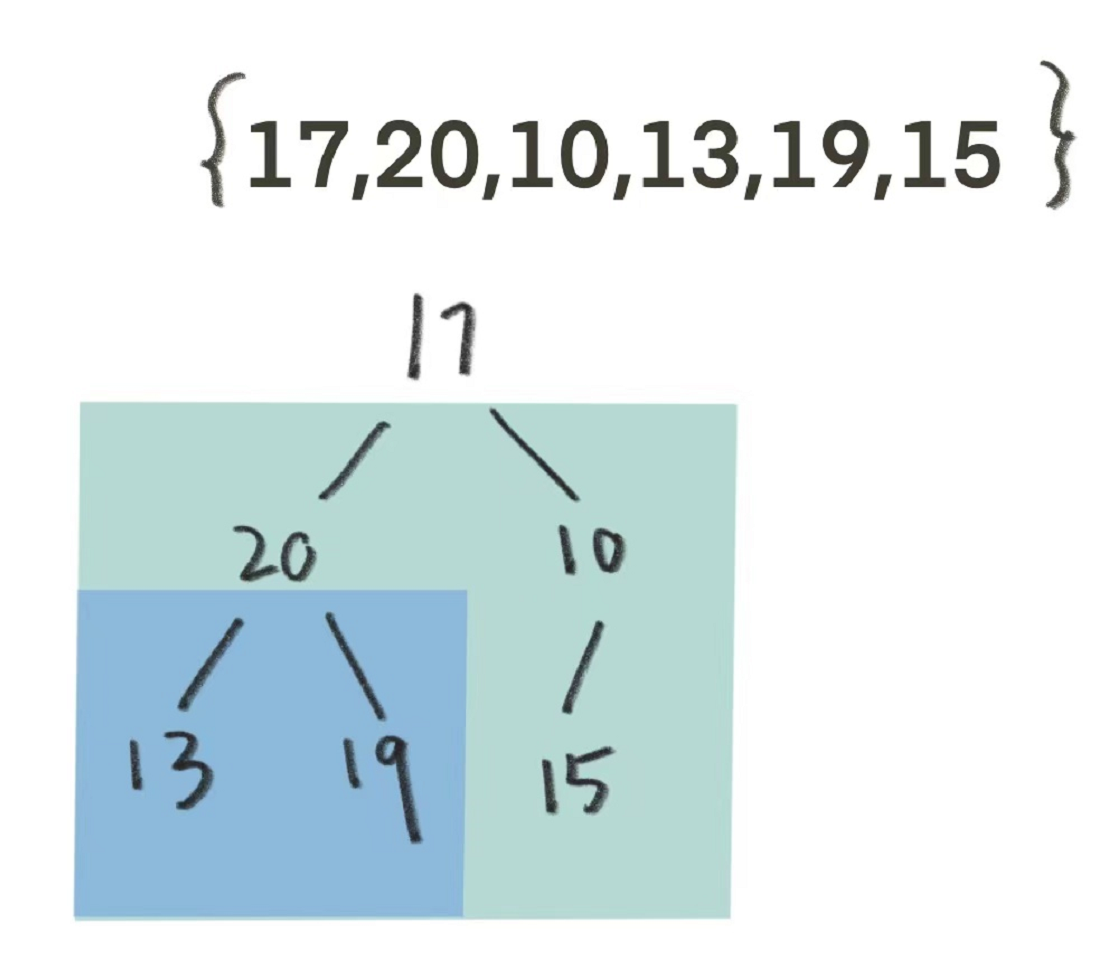
所以我们遇到这样一个问题，为了将17向下调整，得保证它的子树是大堆；而我们要向下调整孩子结点20时，得保证20的子树是大堆……

那么我们可以改变一下思路，从最后一个结点的父节点开始向下调整，大的往上放建大堆。

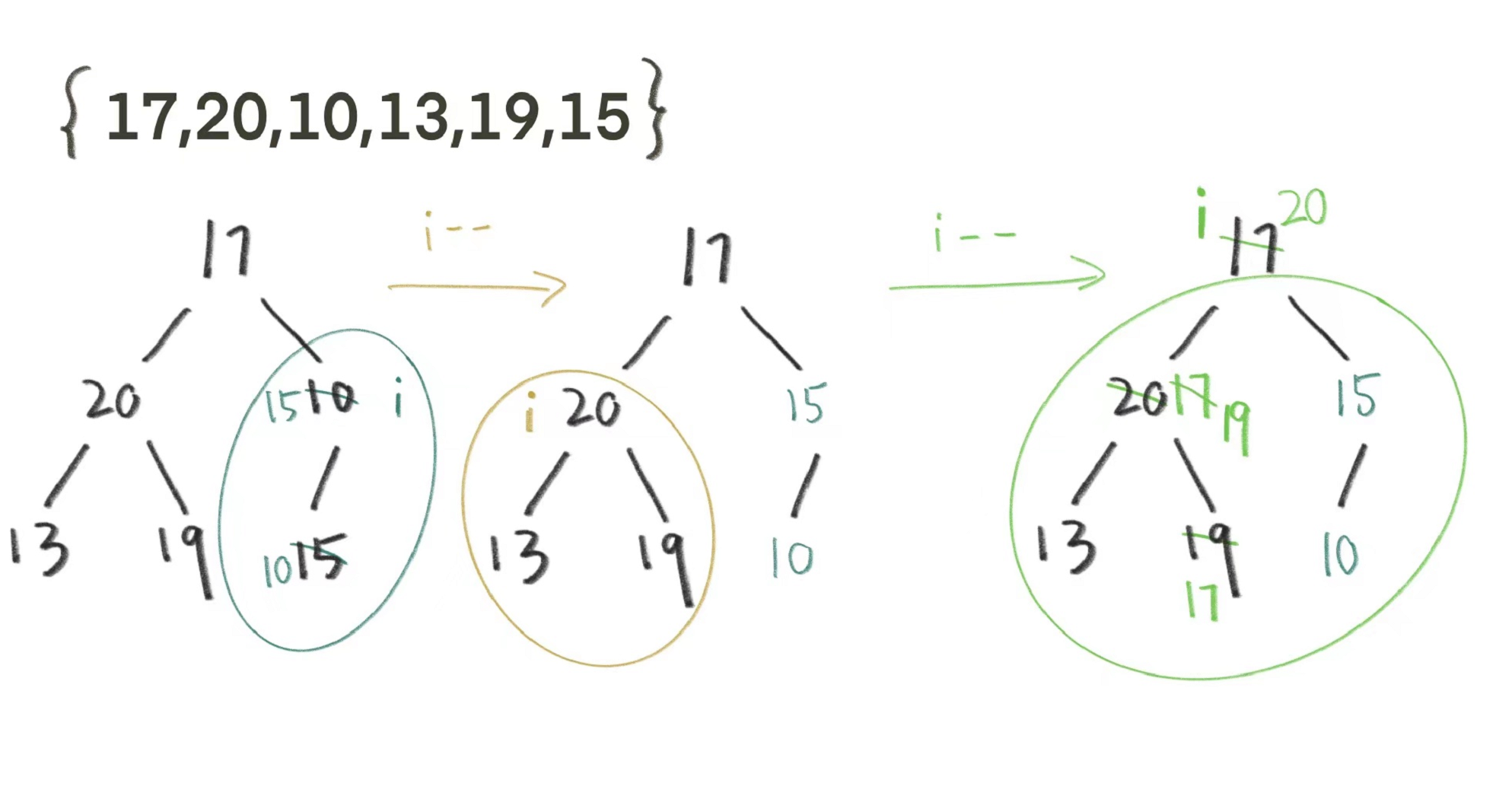
i就是我们目前要向下调整的下标，i首先从最后一个结点的父节点开始；调整完后i–来到20的位置，向下调整后再次i–来到了17的位置，向下调整，这里会调整两层。最后我们就得到了一个大堆。

所以我们其实是从子树开始调整，然后保证堆顶的子树为堆后再将其进行向下调整。

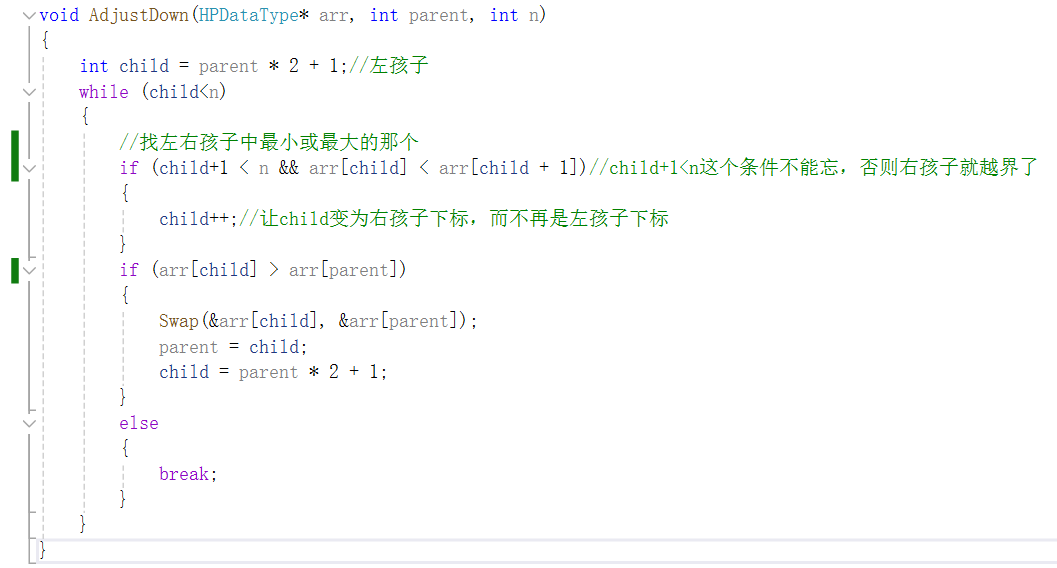
代码：

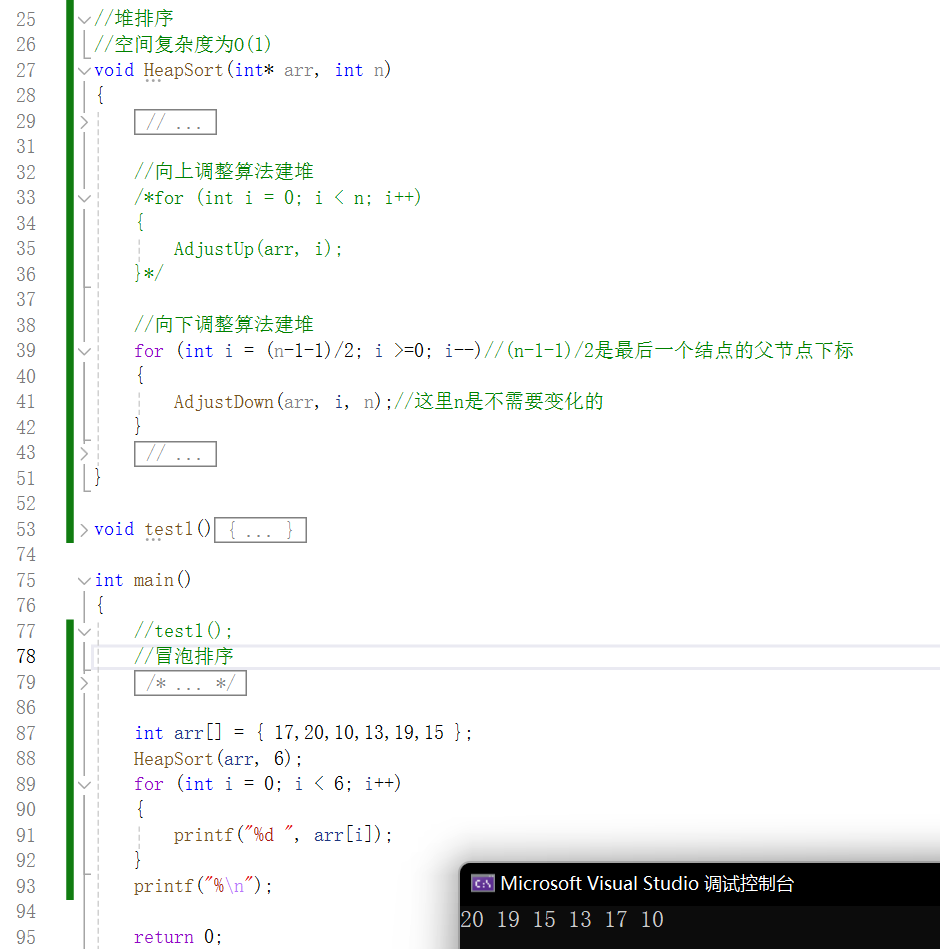
可以看到，我们的大堆就成功建成了。

这就是我们的向下调整算法建堆。

可以看到向上调整算法建堆时我们就是从头（第一个数据）开始，而向下调整算法建堆我们则是从尾开始（最后一个结点的父节点）。

---

向上调整算法建堆VS向下调整算法建堆

这两种建堆算法，哪一种的时间复杂度更好呢？

我们需要数学推理。

向下调整算法建堆的时间复杂度推理

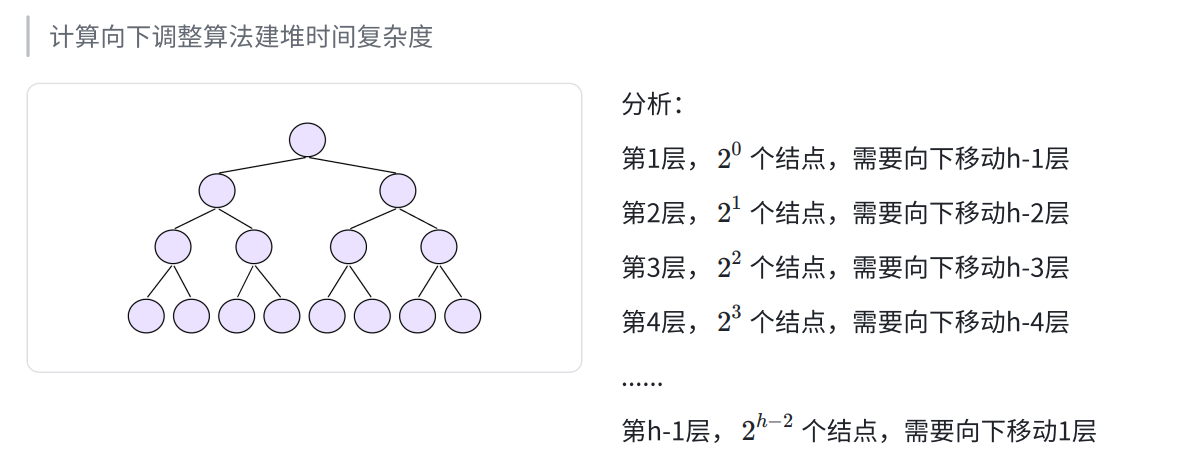
（我们只看到h-1层为止，因为最后一层不需要向下调整；h代表的是总层数；需要移动的层数是最坏情况的移动层数）

如图，要计算移动的次数是由结点的数量和移动的层次共同决定的，我们在二叉树的性质中可以得知每一层的最大节点数（每一层的节点数要移动的层数是不同的所以我们要分开去看），而层数我们也是可以知道的。

我们时间复杂度计算的是最坏的情况，所以我们可以这样计算需要移动的总步数：$每层节点个数\times 向下调整次数$，最后加在一起。

然后我们通过错位相减，化简，再通过二叉树性质，代入可以得到$T(n)=n-lo{g}_2(n+1)$。我们知道时间复杂度最后取对结果影响最大的那个，所以向下调整算法建堆我们最后得到的时间复杂度为$O(n)$。

（详细推理见下图）

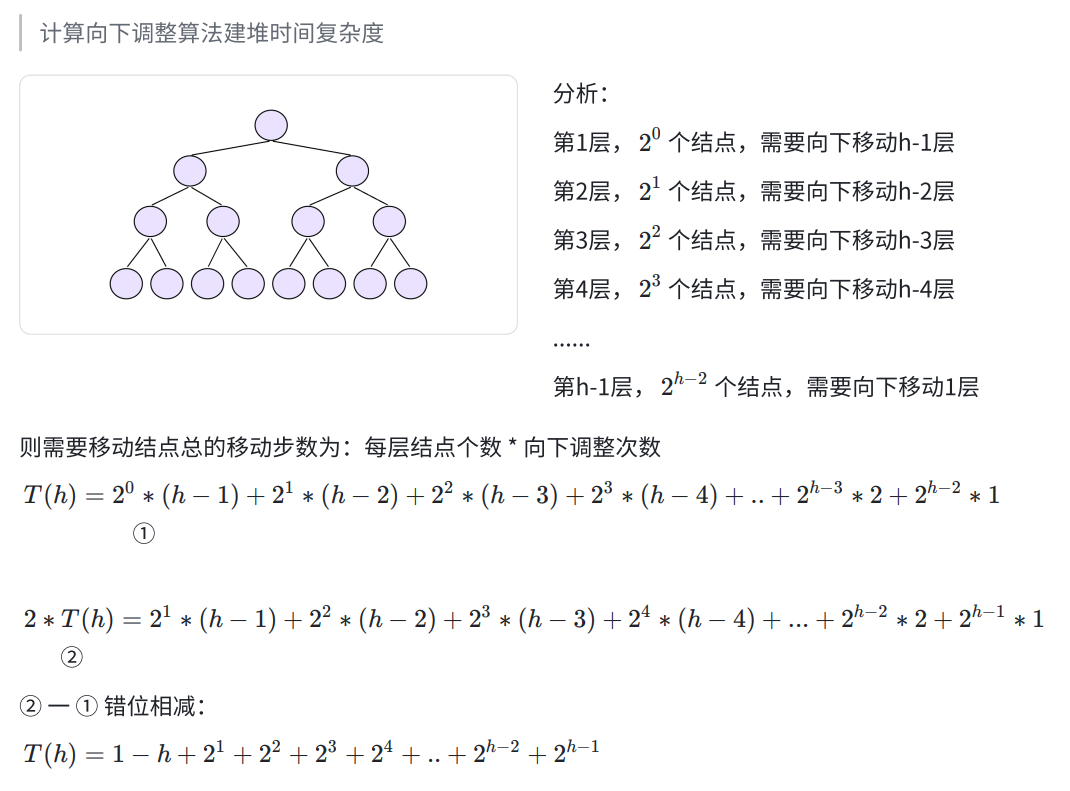
用我们刚才乍一看的方法，外层循环大概为O(n)，内层的AdjustDown方法根据二叉树的性质：$2^k-1=n$; $k=lo{g}_2(n+1)$，为O(logn)，所以我们推测为O(nlogn)，但实际上根据数学推导却是O(n)。

可以看到，我们如果乍一看，其实错误地算大了许多。

向上调整算法建堆的时间复杂度推理

同样的，因为是最坏情况，我们同样是计算每层的节点个数×每层结点要移动的层数，最后相加。

根节点无需向上调整，从第二层开始调整。

最后同样是错位相减、化简，利用性质替换，我们得到向上调整算法建堆的时间复杂度为$O(n\ast lo{g}_{2}n)$。

（详细推理）

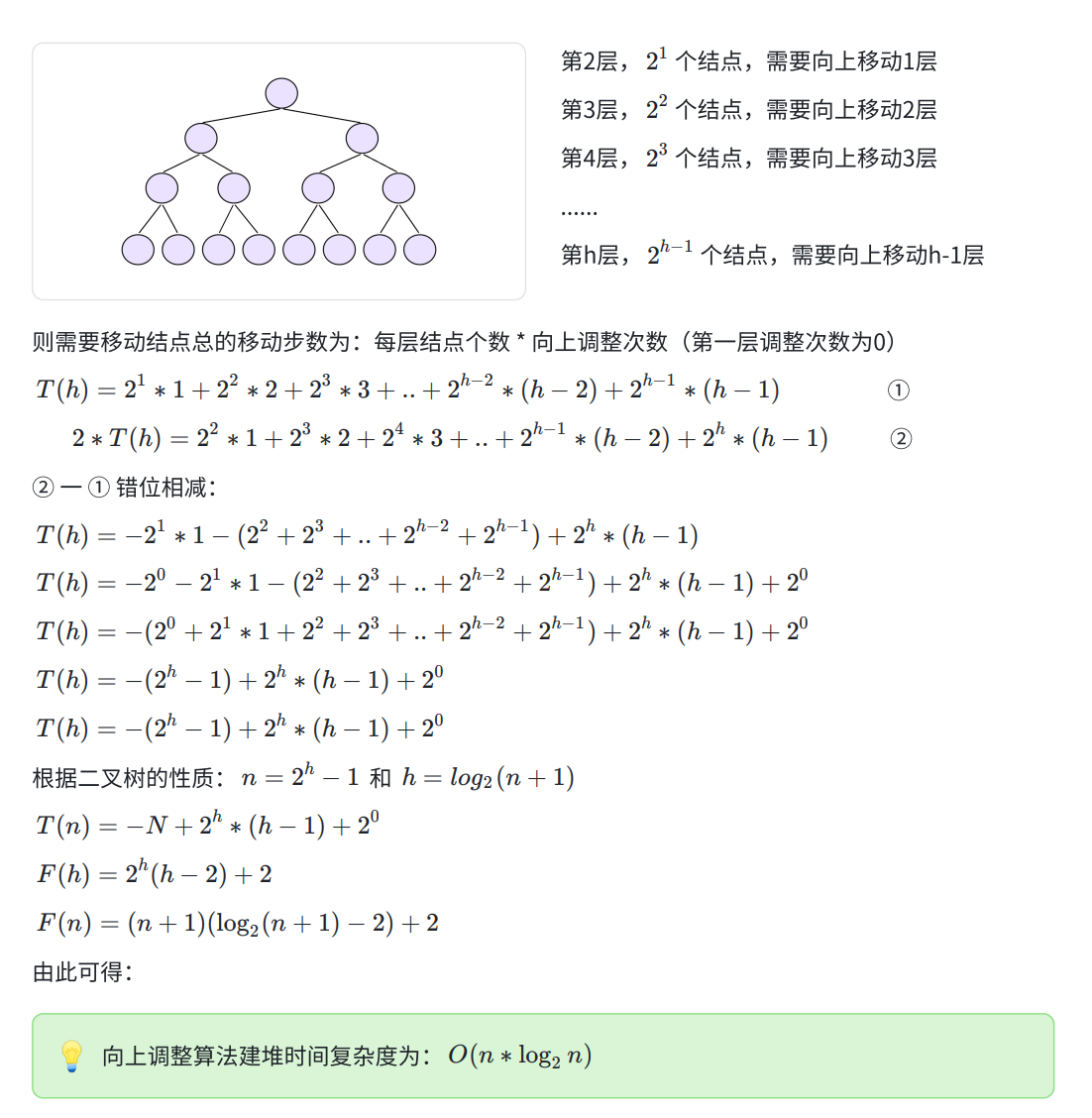
我们可以看出，对于向上调整算法建堆来说，越往下结点数越多，需要移动的层次也越多；向下调整算法建堆则越往上虽然要移动层次越多，但是节点数却越少。

移动层数越多×节点数越多，显然要比移动层次越多×节点数越少来得多。

所以我们凭借这个规律我们其实也可以就看出向下调整算法建堆的时间复杂度应该是更低的。

所以，无论是从时间复杂度的结果还是从这个规律来看，向下调整算法建堆的时间复杂度是更好的。

---

过了这么久我们再说回堆排序，所以比较好的堆排序方法就是使用向下调整算法建堆加上循环将堆顶数据与当前的最后一个数据交换。

我们可以知道堆排序的时间复杂度就为向下调整算法建堆的O(n)，加上后一个循环中用到向下调整方法复杂度为O(logn)，所以整个循环复杂度为O(nlogn)，O(n)+O(nlogn)，取大的那个，所以堆排序的时间复杂度为O(n*logn)。

到此，本文结束，祝阅读愉快O(∩_∩)O

原文地址：https://blog.csdn.net/2301_82135086/article/details/140696613

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！