【高中数学/对数函数,指数函数】设方程10^x=|lg(-x)|的两根分别为x1,x1,则以下四选项正确的是? (PS:牛顿中值法失效的案例)
【问题】
设方程10^x=|lg(-x)|的两根分别为x1,x1,则以下四选项正确的是?
A.x1*x2<0
B.x1*x2=0
C.x1*x2>1
D.0<x1*x2<1
【解答】
10^x=|lg(-x)|的两根,即函数y=10^x与y=|lg(-x)|的两个交点。
函数y=10^x的曲线无须赘述,y=|lg(-x)|才是中点。
考虑到对数的真数必须大于0,故y=|lg(-x)|的定义域只能取x负半轴即(-∞,0),它的曲线像是把y=lgx的选线先以y轴为对称轴向右翻折一次。
又考虑到绝对值符号,故轴以下的部分还需要以x轴为对称轴向上翻折一次。
最终两图线就是以下模样:
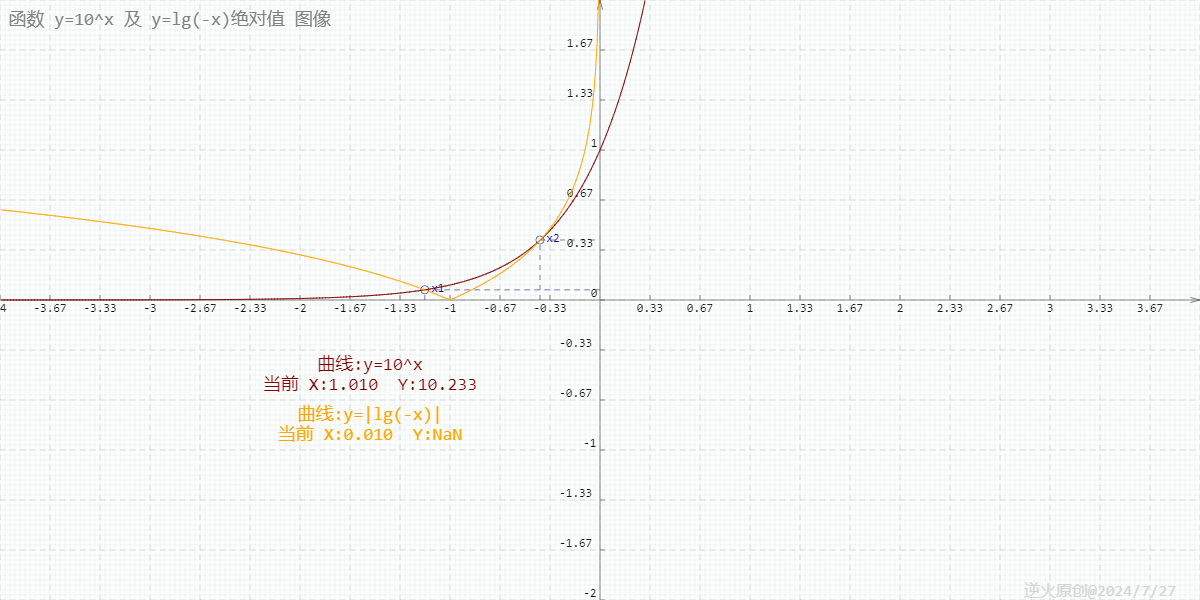
通过上图可以看到,两个根都在第二象限内,故排除AB。
CD的差别是x1*x2是大于1还是小于1的问题,这个问题可如下求解。
| 符号 | 表达式 | 说明 |
| |lg(-x1)|=10^x1,|lg(-x2)|=10^x2 | 两曲线交点的横纵坐标都相同 | |
| => | 10^x1<10^x2 | 指数函数的单调递增性质 |
| => | |lg(-x1)|<|lg(-x2)| | |
| => | lg(-x1)<-lg(-x2) | 去绝对值 |
| => | lg(-x1)<lg(1/-x2) | 系数变指数 |
| => | -x1<1/-x2 | 去lg符号 |
| => | x1*x2<1 | 两边同乘-x2 |
因此,最终答案选D。
【绘图所用Canvas代码】
<!DOCTYPE html>
<html lang="utf-8">
<meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>
<head>
<title>UNASSIGNED</title>
<style type="text/css">
.centerlize{
margin:0 auto;
border:0px solid red;
width:1200px;height:600px;
}
</style>
</head>
<body οnlοad="draw();">
<div class="centerlize">
<canvas id="myCanvas" width="10px" height="10px" style="border:1px dashed black;">
如果看到这段文字说您的浏览器尚不支持HTML5 Canvas,请更换浏览器再试.
</canvas>
</div>
</body>
</html>
<script type="text/javascript">
<!--
/*****************************************************************
* 将全体代码拷贝下来,粘贴到文本编辑器中,另存为.html文件,
* 再用chrome浏览器打开,就能看到动画效果。
******************************************************************/
// 系统常量定义处
const TITLE="函数 y=10^x 及 y=lg(-x)绝对值 图像"; // 图像标题
const WIDTH=1200; // 画布宽度
const HEIGHT=600; // 画布高度
const SCALE_UNIT=150; // 缩放比例
// 系统变量定义处
var context=0; // 画布环境
var stage; // 舞台对象
var timeElapsed=0; // 动画运作的的时间
const TIME_END=100000; // 动画运作的期限
//-------------------------------
// Canvas开始运作,由body_onload调用
//-------------------------------
function draw(){
document.title=TITLE;
// 画图前初始化
var canvas=document.getElementById('myCanvas');
canvas.width=WIDTH;
canvas.height=HEIGHT;
context=canvas.getContext('2d');
// 进行屏幕坐标系到笛卡尔坐标系的变换
// 处置完成前,原点在左上角,向右为X正向,向下为Y的正向
// 处置完毕后,原点移动到画布中央,向右为X正向,向上为Y的正向
context.translate(WIDTH/2,HEIGHT/2);
context.rotate(Math.PI);
context.scale(-1,1);
// 初始化舞台
stage=new Stage();
// 开始动画
animate();
};
//-------------------------------
// 画图
//-------------------------------
function animate(){
timeElapsed+=1;// 时间每轮增加1
stage.update(timeElapsed);
stage.paintBg(context);
stage.paint(context);
if(timeElapsed<TIME_END){
window.requestAnimationFrame(animate);
}
}
//-------------------------------
// 舞台对象定义处
//-------------------------------
function Stage(){
// 内置对象(非必要勿更改)
var obj=new Object;
// 对象下的曲线数组(非必要勿更改)
obj.curves=[];
// 塞入曲线1(按需修改设定项)
obj.curves.push({
name:"曲线:y=10^x",
xEnd:1,
x:-4,
y:0,
setY:function(x){
this.y=Math.pow(10,x);// 解析式
let coord={"x":x,"y":this.y};
this.pts0.push(coord);
},
"pts0":[],
});
// 塞入曲线2(按需修改设定项)
obj.curves.push({
name:"曲线:y=|lg(-x)|",
xEnd:0,
x:-4,
y:0,
setY:function(x){
this.y=Math.abs(Math.log(-x)/Math.log(10));// 解析式
let coord={"x":x,"y":this.y};
this.pts0.push(coord);
},
"pts0":[],
});
// 随时间更新位置(非必要勿更改)
obj.update=function(t){
for(var i=0;i<this.curves.length;i++){
var curve=this.curves[i];
if(curve.x<curve.xEnd){
curve.x+=0.01;
curve.setY(curve.x);
}
}
};
// 画前景
obj.paint=function(ctx){
// 手动标记点
paintPoint(ctx,-1.168,0.0679,"x1","navy");
paintPoint(ctx,-0.40,0.40,"x2","navy");
//paintPoint(ctx,6,-4,"d","navy");
// 文字左上角位置(可手动修改设定值)
const X_START=-230; // 文字横起点
const Y_START=-75; // 文字纵起点
const OFFSET=50; // 文字间隔
// 遍历曲线数组(非必要勿更改)
for(var i=0;i<this.curves.length;i++){
var curve=this.curves[i];
var color=getColor(i);
// 曲线名称
drawText(ctx,curve.name,X_START,Y_START-i*OFFSET,color,18);
// 曲线当前点坐标
drawText(ctx,"当前 X:"+curve.x.toFixed(3)+" Y:"+curve.y.toFixed(3),X_START,Y_START-20-(i)*OFFSET,color,18);
// 绘制曲线
if(curve.pts0){
paintCurve(ctx,color,curve.pts0);
// 绘制曲线分段1的高低点(可选)
//var mm=findMaxMin(curve.pts0);
//markMaxMin(ctx,mm,color);
}
if(curve.pts1){
paintCurve(ctx,color,curve.pts1);
// 绘制曲线分段2的高低点(可选)
//var mm=findMaxMin(curve.pts1);
//markMaxMin(ctx,mm,color);
}
if(curve.pts2){
paintCurve(ctx,color,curve.pts2);
// 绘制曲线分段3的高低点(可选)
//var mm=findMaxMin(curve.pts2);
//markMaxMin(ctx,mm,color);
}
if(curve.pts3){
paintCurve(ctx,color,curve.pts3);
// 绘制曲线分段4的高低点(可选)
//var mm=findMaxMin(curve.pts3);
//markMaxMin(ctx,mm,color);
}
}
};
// 画背景(非必要不更改)
obj.paintBg=function(ctx){
// 清屏
ctx.clearRect(-600,-300,1200,600);
ctx.fillStyle="rgb(251,255,253)";
ctx.fillRect(-600,-300,1200,600);
// 画X轴
drawAxisX(ctx,-600,600,50);
// 画Y轴
drawAxisY(ctx,-300,300,50);
// 画网格线
drawGrid(ctx,-600,-300,50,1200,600,50);
// 左上角标题
var metrics = ctx.measureText(TITLE);
var textWidth = metrics.width;
drawText(ctx,TITLE,-WIDTH/2+textWidth+3,HEIGHT/2-30,"grey",18);
// 右下角作者,日期
const waterMarkTxt="逆火原创@"+(new Date()).toLocaleDateString();
metrics = ctx.measureText(waterMarkTxt);
textWidth = metrics.width;
drawText(ctx,waterMarkTxt,WIDTH/2-textWidth,-HEIGHT/2,"lightGrey",16);
};
return obj;
}
// 描绘并标识一个点
function paintPoint(ctx,x,y,text,color){
var xReal=x*SCALE_UNIT;
var yReal=y*SCALE_UNIT;
ctx.strokeStyle=color;
ctx.lineWidth=0.5;
// 划线
ctx.save();
ctx.setLineDash([5,5]);
ctx.beginPath();
ctx.moveTo(xReal,0);
ctx.lineTo(xReal,yReal);
ctx.lineTo(0,yReal);
ctx.stroke();
ctx.restore();
// 画圈
ctx.beginPath();
ctx.arc(xReal,yReal,4,0,Math.PI*2,false);
ctx.closePath();
ctx.stroke();
// 写文字
var metrics = ctx.measureText(text);
var textWidth = metrics.width;
drawText(ctx,text,xReal+textWidth+2,yReal-5,color,12);
}
// 连点成线画曲线
function paintCurve(ctx,color,cds){
ctx.save();
ctx.strokeStyle = color;
ctx.lineWidth=1;
ctx.beginPath();
for(var i=0; i<cds.length; i++){
let y=cds[i].y;
if(Math.abs(cds[i].y*SCALE_UNIT)<300){
ctx.lineTo(cds[i].x*SCALE_UNIT,cds[i].y*SCALE_UNIT);
}
}
ctx.stroke();
ctx.restore();
}
// 找到坐标数组的最大最小值
function findMaxMin(cds){
if(cds.length<1){
return null;
}
var retval={max:-10000,max_x:0,min:10000,min_x:0};
for(var i=0;i<cds.length;i++){
var y=cds[i].y;
if(y>retval.max){
retval.max=y;
retval.max_x=cds[i].x;
}
if(y<retval.min){
retval.min=y;
retval.min_x=cds[i].x;
}
}
return retval;
}
// 绘出最大最小值
function markMaxMin(ctx,mm,color){
if(mm==null){
return;
}
// 最大值
var x=mm.max_x;
var y=mm.max;
ctx.strokeStyle=color;
ctx.beginPath();
ctx.arc(x*SCALE_UNIT,y*SCALE_UNIT,5,0,Math.PI*2,false);
ctx.closePath();
ctx.stroke();
var text="max@x="+x.toFixed(3)+" y="+y.toFixed(3);
drawText(ctx,text,x*SCALE_UNIT,y*SCALE_UNIT,color,12);
// 最小值
var x=mm.min_x;
var y=mm.min;
ctx.strokeStyle=color;
ctx.beginPath();
ctx.arc(x*SCALE_UNIT,y*SCALE_UNIT,5,0,Math.PI*2,false);
ctx.closePath();
ctx.stroke();
var text="min@x="+x.toFixed(3)+" y="+y.toFixed(3);
drawText(ctx,text,x*SCALE_UNIT,y*SCALE_UNIT,color,12);
}
// 定点画实心圆
function drawSolidCircle(ctx,x,y,r,color){
ctx.save();
ctx.beginPath();
ctx.arc(x,y,r,0,2*Math.PI);
ctx.fillStyle=color;
ctx.fill();
ctx.restore();
}
// 两点之间画线段
function drawLine(ctx,x1,y1,x2,y2,color){
ctx.save();
ctx.lineWidth=0.25;
ctx.strokeStyle=color;
ctx.beginPath();
ctx.moveTo(x1,y1);
ctx.lineTo(x2,y2);
ctx.stroke();
ctx.closePath();
ctx.restore();
}
// 画横轴
function drawAxisX(ctx,start,end,step){
const AXISY_COLOR="black";
ctx.save();
ctx.lineWidth=0.5;
ctx.strokeStyle=AXISY_COLOR;
// 画轴
ctx.beginPath();
ctx.moveTo(start, 0);
ctx.lineTo(end, 0);
ctx.stroke();
ctx.closePath();
// 画箭头
ctx.beginPath();
ctx.moveTo(end-Math.cos(getRad(15))*10, Math.sin(getRad(15))*10);
ctx.lineTo(end, 0);
ctx.lineTo(end-Math.cos(getRad(15))*10, -Math.sin(getRad(15))*10);
ctx.stroke();
ctx.closePath();
// 画刻度
var x,y;
y=5;
for(x=start;x<end;x+=step){
if(x==0){
continue;
}
ctx.beginPath();
ctx.moveTo(x, 0);
ctx.lineTo(x, y);
ctx.stroke();
ctx.closePath();
var text=formatScale(x/SCALE_UNIT);
drawText(ctx,text,x,y-20,AXISY_COLOR,12);
}
ctx.restore();
}
// 画纵轴
function drawAxisY(ctx,start,end,step){
const AXISY_COLOR="black";
ctx.save();
ctx.lineWidth=0.5;
ctx.strokeStyle=AXISY_COLOR;
// 画轴
ctx.beginPath();
ctx.moveTo(0, start);
ctx.lineTo(0, end);
ctx.stroke();
ctx.closePath();
// 画箭头
ctx.beginPath();
ctx.moveTo(Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
ctx.lineTo(0, end);
ctx.lineTo(-Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
ctx.stroke();
ctx.closePath();
// 画刻度
var x,y;
x=5;
for(y=start;y<end;y+=step){
ctx.beginPath();
ctx.moveTo(x, y);
ctx.lineTo(0, y);
var text=formatScale(y/SCALE_UNIT);
var metrics = ctx.measureText(text);
var textWidth = metrics.width;
drawText(ctx,text,x-textWidth-5,y,AXISY_COLOR,12);
ctx.stroke();
ctx.closePath();
}
ctx.restore();
}
//-------------------------------
// 得到整型后的刻度
//-------------------------------
function formatScale(scale){
var s=scale*10;
if(s % 5==0){
return scale+"";
}else{
return scale.toFixed(2);
}
}
// 画网格线
function drawGrid(ctx,x1,y1,step1,x2,y2,step2){
ctx.save();
ctx.lineWidth=0.25;
ctx.strokeStyle="lightgrey";
// 分十格
var x,y;
for(x=x1;x<x2;x+=step1/10){
ctx.beginPath();
ctx.moveTo(x, y1);
ctx.lineTo(x, y2);
ctx.stroke();
ctx.closePath();
}
for(y=y1;y<y2;y+=step2/10){
ctx.beginPath();
ctx.moveTo(x1, y);
ctx.lineTo(x2, y);
ctx.stroke();
ctx.closePath();
}
// 十小格间的分割线
ctx.lineWidth=0.25;
ctx.strokeStyle="grey";
ctx.setLineDash([5,5]);// 设置虚线,起止点间包含五空格五划线共十段
for(x=x1;x<x2;x+=step1){
ctx.beginPath();
ctx.moveTo(x, y1);
ctx.lineTo(x, y2);
ctx.stroke();
}
for(y=y1;y<y2;y+=step2){
ctx.beginPath();
ctx.moveTo(x1, y);
ctx.lineTo(x2, y);
ctx.stroke();
}
ctx.restore();
}
//-------------------------------
// 角度得到弧度
//-------------------------------
function getRad(degree){
return degree/180*Math.PI;
}
//-------------------------------
// 得到颜色
//-------------------------------
function getColor(index){
var arr=[
"maroon" /* maroon 棕色*/,
"orange" /* orange 橙色*/,
"blue" /* blue蓝色*/,
"green" /* green 绿色*/,
"fuchsia"/* fuchsia 紫红*/,
"grey" /* grey 草木灰*/,
"lime" /* lime 亮绿色*/,
"navy" /* navy 海军蓝*/,
"purple" /* purple 紫色*/,
"skyblue"/* skyblue 天蓝*/,
"teal" /* teal 蓝绿色*/,
"yellow" /* yellow 亮黄*/,
"aqua" /* aqua湖绿色*/,
"red" /* red 大红*/,
"#88815d"/* 雪松*/,
"#4f876c"/* 伊甸园绿*/,
"#97572b"/* 皮革褐*/,
"#b79777"/* 卡其*/,
"#d7ccb6"/* 象牙白*/,
"#414142"/* 木炭艺术*/,
"#764136"/* 焦棕*/,
"#46515a"/* 深板岩*/,
"#3c281e"/* 巧克力*/,
"#681414"/* 铁锈红*/,
"black" /* black黑色*/,
];
return arr[index % arr.length];
}
//-------------------------------------
// 绘制文字,指定颜色
// ctx:绘图环境
// text:文字
// x,y:坐标
// color:颜色
// size:字体大小
//-------------------------------------
function drawText(ctx,text,x,y,color,size){
ctx.save();
ctx.translate(x,y)
ctx.rotate(getRad(180))
ctx.scale(-1,1)
ctx.textBaseline="bottom";
ctx.textAlign="center";
ctx.fillStyle=color;
ctx.font = size+"px consolas";
ctx.fillText(text,0,0);
ctx.restore();
}
// JS开立方
function kaiLiFang(x){
if(x>0){
return Math.pow(x,1/3);
}else{
return -Math.pow(-x,1/3);
}
}
//-->
/**************************************
以下节选自某剧中王志文的台词:
我现在已经不和别人争吵了,
因为我开始意识到,
每个人只能站在自己的认知角度上去思考问题。
所以,如果有人跟你说一加一等于三,
你只需笑着对他说:是的,你真厉害!
有钱人把人做好,没钱就把事儿做好。
蛇不知道自己有毒,人不知道自己有错。
你的好对别人就像一颗糖,吃了就没了;
你的不好就像一道伤疤,它会永远存在。
彼此认知不同,就不必争辩;
彼此三观不合,就不必同行。
**************************************/
</script>
【求根的方法】
图上可见x1,x2被标识了出来,其坐标是(-1.168,0.0679),(-0.40,0.40),前者是用牛顿中值法算得,后者是在中值法失效后目测所得,看来牛顿法比较适合两曲线碰撞相交,在曲线渐近相交时力有未逮。
成功执行的求根代码:
package test240727;
/**
* 牛顿中值法求根
* @author 逆火
*
*/
public class Test {
public static void main(String[] args) {
double start=-1.33f;
double end =-0.99f;
double result=99;
int idx=0;
while(Math.abs(result)>0.000001){
double mid=(start+end)/2;
result=Math.pow(10,mid)-Math.abs(Math.log(-mid)/Math.log(10));//解析式
idx++;
System.out.println("#"+idx+".strat="+format(start)+" mid="+format(mid)+" end="+format(end)+" result="+format(result));
if(result>0){
end=mid;
}else{
start=mid;
}
}
System.out.println("使用牛顿中值法求得根="+end);
}
/**
* 返回保留五位小数的字符串
* @param d
* @return
*/
public static String format(double d){
java.text.DecimalFormat df =new java.text.DecimalFormat("#0.00000");
return df.format(d);
}
}
成功执行的结果:
#1.strat=-1.33000 mid=-1.16000 end=-0.99000 result=0.00473 #2.strat=-1.33000 mid=-1.24500 end=-1.16000 result=-0.03828 #3.strat=-1.24500 mid=-1.20250 end=-1.16000 result=-0.01735 #4.strat=-1.20250 mid=-1.18125 end=-1.16000 result=-0.00646 #5.strat=-1.18125 mid=-1.17063 end=-1.16000 result=-0.00091 #6.strat=-1.17063 mid=-1.16531 end=-1.16000 result=0.00190 #7.strat=-1.17063 mid=-1.16797 end=-1.16531 result=0.00049 #8.strat=-1.17063 mid=-1.16930 end=-1.16797 result=-0.00021 #9.strat=-1.16930 mid=-1.16863 end=-1.16797 result=0.00014 #10.strat=-1.16930 mid=-1.16896 end=-1.16863 result=-0.00003 #11.strat=-1.16896 mid=-1.16880 end=-1.16863 result=0.00006 #12.strat=-1.16896 mid=-1.16888 end=-1.16880 result=0.00001 #13.strat=-1.16896 mid=-1.16892 end=-1.16888 result=-0.00001 #14.strat=-1.16892 mid=-1.16890 end=-1.16888 result=0.00000 #15.strat=-1.16892 mid=-1.16891 end=-1.16890 result=-0.00000 #16.strat=-1.16891 mid=-1.16891 end=-1.16890 result=-0.00000 #17.strat=-1.16891 mid=-1.16891 end=-1.16890 result=-0.00000 使用牛顿中值法求得根=-1.1689026149906567
不成功求根的代码:
package test240727;
/**
* 牛顿中值法求根
* @author 逆火
*
*/
public class Test {
public static void main(String[] args) {
double start=-0.67f;
double end =-0.33f;
double result=99;
int idx=0;
while(Math.abs(result)>0.000001){
double mid=(start+end)/2;
result=Math.pow(10,mid)-Math.abs(Math.log(-mid)/Math.log(10));//解析式
idx++;
System.out.println("#"+idx+".strat="+format(start)+" mid="+format(mid)+" end="+format(end)+" result="+format(result));
if(result>0){
end=mid;
}else{
start=mid;
}
}
System.out.println("使用牛顿中值法求得根="+end);
}
/**
* 返回保留五位小数的字符串
* @param d
* @return
*/
public static String format(double d){
java.text.DecimalFormat df =new java.text.DecimalFormat("#0.00000");
return df.format(d);
}
}
两处代码只有起止点不同,但一个能算出来一个算不出来,只能说明中值法求根还有不完善的地方。
END
原文地址:https://blog.csdn.net/River_Sun/article/details/140736665
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
