因果推断 | 双重机器学习（DML）算法原理和实例应用

1 引言

小伙伴们，好久不见呀。

距离上次更新已经过去了一个半月，上次发文章时还信誓旦旦地表达自己后续目标是3周更新一篇文章，然后马上就打脸了。

其实第3周的时候，有想过把当时的一些学习心得总结一下，先发出来。但是宁缺毋滥的理性很快打败了内心的小心机，毕竟骗自己的态度不可取。看清目标与现实间的差异，逐渐认识自身有限的学习能力，本身也是一种收获。

回到文章本身，今天要说的主题是：一种结合机器学习做因果推断任务的算法，学术名叫Double Machine Learning（DML），双重机器学习。

围绕DML，本文将首先介绍DML的算法原理；然后使用简单的模拟数据手动实现该算法，并和已有的工具包做对比，以此加深对该算法的理解；在此基础上，针对更实际的案例，尝试求解物理意义更强的因果推断问题。

正文见下。

2 DML算法原理

2.1 问题阐述

先回顾一下潜在因果框架中因果推断问题的定义：样本数据集为： D = { d 1 , d 2 , . . . , d n } D=\{d_1,d_2,...,d_n\} D={d1​,d2​,...,dn​}，$n$为样本数量；策略变量为 T ∈ { 0 , 1 } T\in \{0, 1\} T∈{0,1}，$T=0$表示不施加策略，$T=1$表示施加策略；协变量$X$，一般指与策略无关的变量；结果变量$Y$：$Y_{0i}$表示无策略时第$i$个样本的结果变量，$Y_{1i}$表示有策略时第$i$个样本的结果变量。目标是：基于数据集 D = { T i , X i , Y i } i n D=\{T_i,X_i,Y_i\}_i^n D={Ti​,Xi​,Yi​}in​，估计$T$和$Y$之间的因果效应。

在这个定义里面，有个前提假设很容易不满足，那就是$X$和$T$无关。一方面，在寻找$X$时，很难确认$X$和$T$无关。举个例子，我们想知道冰淇淋的价格与销量间的因果效应，此处$T$是价格，$Y$是销量。$X$很容易想到有：当时的天气温度、当地的生活水平等等。但当地的生活水平和价格之间大概率是正相关的，比如同一款巧乐兹在北京卖的价格和十八线小城市的价格，大概率是有差别的。

另一方面，为了更全面考虑问题，变量$X$中会纳入尽可能多的特征，而特征越多，就越难保证其和策略变量$T$是否相关。

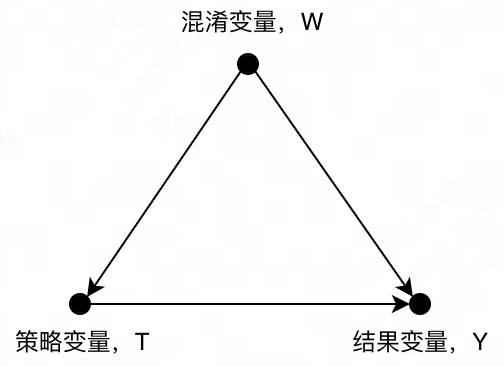
当$X$和$T$相关后，就会产生混淆变量$W$，该类变量既影响$Y$，又影响$T$，如下图所示。

在此情况下，要得到$T$和$Y$之间纯净的因果效应就更难了。

2.2 DML算法

为了解决包含混淆变量的因果推断问题，本节介绍一种被称为双重机器学习的算法，英文是：Double Machine Learning (DML)。

该算法考虑如下一种线性模型：
$$Y=T{\theta }_0+X{\beta }_0+U,E[U(X,T)]=0$$
$$T=X{\gamma }_0+V,E[V|X]=0$$
解释一下上述两个公式：第一个公式表达的是$Y$和$T$、$X$之间为线性关系，其中$U$为随机扰动项；第二个公式表达的是$T$和$X$之间也是线性关系，其中$V$是为随机扰动项。

在该模型中，变量$X$会同时影响$T$和$Y$，即$X$被看做一个混淆变量，只是限定了变量间为线性关系。

DML的算法方案分为两步：第一步是基于机器学习模型使用协变量$X$分别拟合$Y$和$T$，得到$\hat{Y},\hat{T}$，此时残差分别为$Y-\hat{Y}$和$T-\hat{T}$；

第二步是对残差，用任意机器学习模型(很多是最小二乘法)拟合，得到参数$\tau$，即认为是$T$和$Y$之间的真正因果效应值。

$$(Y-\hat{Y})=\tau \cdot (T-\hat{T})$$

DML算法不复杂，不过有几点需要额外说明：

(1) 基于对$T$和$Y$残差的拟合，可以得到真正的因果效应值，直观上可以理解为：先剔除$X$的影响后，再评估$T$和$Y$的因果效应，就会比较纯粹；理论上也是有证明的，只不过其推导证明对我来说有些复杂了，感兴趣的同学可以参考原文献：Double/debiased machine learning for treatment and structural parameters。B站上和CSDN上也有关于这篇文章的部分讲解，都可以参考一下。

(2) DML有个基本假设是：$T$和$Y$之间是线性关系。所以如果$T$不是0/1变量，而是个连续值，那么得到的因果效应值仅在$T$附近有效。例如在上文提到的冰淇淋价格和销量的因果推断问题中，$T$是价格，$Y$是销量，设定$\tau =2$，我们可以说价格减少1个单位后销量能增加2个单位，但如果价格减少10个单位，就不能确认销量是否可以增加20个单位。

(3) 原问题中，$X$中有混杂变量$W$；DML模型中，并没有刻意区分$W$和$X$。而且在实际操作时，由于拟合残差时使用的是机器学习模型，也不必仔细区分每个$X$是不是混杂变量，直接扔进模型就行。

3 DML代码实现

本节通过两个实例，描述如何将DML应用于求解实际的业务问题。考虑到DML其中一种版本——因果森林DML，在业界很常用，本文也会更多关注因果森林DML的实践应用。

3.1 策略变量为0/1变量

策略变量为0/1变量是标准的因果推断问题，所以从这类问题入手比较适合。

本节的问题实例是个虚拟的合成数据，实现函数是causalml.dataset.synthetic_data，这是causalml自带的数据集，而causalml是Uber开源的因果推断工具包，未来肯定还会经常遇到它。

针对这个问题实例，下面的代码分别使用三种策略实现因果森林DML的技术方案：

(1) 自己编写代码实现。在计算$Y$和$T$的残差时，使用sklearn.ensemble.RandomForestRegressor；在拟合残差时，使用sklearn.linear_model.LinearRegression。

(2) 工具包+手动设置机器学习模型。工具包使用econml.dml.DML，然后依次设置计算残差和残差拟合的机器学习模型。

(3) 工具包一键完成。直接调用econml.dml.CausalForestDML。

这里的工具包需要单独描述一下。econml是微软开源的因果推断工具包，没有继续使用causalml，是因为causalml中暂时还不支持DML。在econml中，DML可以理解为一个简单框架，允许用户自行设置每个步骤上的机器学习模型；CausalForestDML可以理解为一个已经集成好的因果森林DML。

import pandas as pd
from causalml.metrics import auuc_score, plot_gain
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from causalml.dataset import synthetic_data
from econml.dml import CausalForestDML, DML


# 自编代码实现因果森林DML
def algo_by_self_cf_dml(y, treat, X):
    # 计算y的残差
    rf_y = RandomForestRegressor()
    rf_y.fit(X, y)
    y_res = y - rf_y.predict(X)

    # 计算treat的残差
    rf_t = RandomForestRegressor()
    rf_t.fit(X, treat)
    treat_res = treat - rf_t.predict(X)

    # 计算因果效果
    lr = LinearRegression(fit_intercept=False).fit(treat_res.reshape(-1, 1), y_res.reshape(-1, 1))
    print('self_cf_dml: w = {:.2f}'.format(lr.coef_[0, 0]))


# econml工具包实现因果森林DML
def algo_by_econml_dml(y, treat, X):
    # dml + 手动设置
    dml = DML(model_y=RandomForestRegressor(),
              model_t=RandomForestRegressor(),
              model_final=LinearRegression(fit_intercept=False))
    dml.fit(y, treat, X=X)
    print('DML: {}'.format(dml.ate(X)))

    # 因果森林DML
    cf_dml = CausalForestDML()
    cf_dml.fit(y, treat, X=X)
    print('CausalForestDML: {}'.format(cf_dml.ate(X)))

    return dml, cf_dml


# 计算AUUC和绘制gain曲线
def auuc_score_and_plot(y, treat, X, dml, cf_dml):

    # 使用dataframe组织计算AUUC的必要数据
    df = pd.DataFrame({
        'y': y,
        'treat': treat,
        'cf_dml': cf_dml.effect(X),
        'dml': dml.effect(X)
    })

    # 计算AUUC值
    auuc = auuc_score(df, outcome_col='y', treatment_col='treat', normalize=True, tmle=False)
    print(auuc)

    # 绘制gain曲线
    plot_gain(df, outcome_col='y', treatment_col='treat', normalize=True, random_seed=10, n=100, figsize=(8, 8))


if __name__ == '__main__':
    # 使用synthetic_data生成数据
    y, X, treat, _, _, _ = synthetic_data(mode=1, n=10000, p=8, sigma=1.0)

    # 自编代码实现因果森林DML
    algo_by_self_cf_dml(y, treat, X)

    # econml工具包实现因果森林DML
    dml, cf_dml = algo_by_econml_dml(y, treat, X)

    # 计算AUUC和绘制gain曲线
    auuc_score_and_plot(y, treat, X, dml, cf_dml)

使用多种策略实现因果森林DML，最重要的价值是可以加深对DML算法原理和工具包的理解。结合实践过程和以下的输出结果，可以发现一些新认知：

(1) 前文介绍的DML算法原理中，直接求解得到的$\tau$，看起来应该是平均因果效应$ATE$。
至于如何使用$\tau$去预测新样本的个体因果效应$ITE$，并没有提到；但在econml.dml中，dml.effect(X)却可以得到$ITE$。

(2) 从$ATE$的计算结果上可以看出，三种策略的结果是相似的，说明对DML算法原理的认知是没有多大问题的；第二种策略和第三种策略得到的结果并不完全相同，说明econml.dml.CausalForestDML相比econml.dml.DML，在代码层面还存在一些不同。

(3) 从auuc的结果来看，econml.dml.CausalForestDML的表现显著优于econml.dml.DML。但由于数据是虚拟的，下钻分析的意义不大，就不继续深入了。

关于auuc的计算还需要再描述一下。目前econml不支持针对auuc的计算和绘图，但是causalml可以。所以在代码中，我用到了 causalml.metrics.auuc_score和plot_gain这两个函数。这两个函数需要的数据，至少是2列：第1列是$Y$值，第2列是$T$值，其他的列都会被认为是不同模型输出的因果效应值，然后分别评估和输出。

self_cf_dml: w = 0.47
DML: 0.48424327569296155
CausalForestDML: 0.4705562443255083
cf_dml    0.716144
dml       0.505681
Random    0.498693
dtype: float64

3.2 策略变量为连续变量

通过上一节的实例，我们应该对因果森林DML有一个比较直观的感受了。本节尝试使用该模型解决一个业务场景中经常遇到的问题实例：推断商品价格和销量之间的因果效应。

本节实例的数据来源是kaggle竞赛中提供的在线零售销售数据。train_test_date_split函数参考其他内容对原始数据做了预处理，这部分的内容和因果森林DML无关，可以略过其中的逻辑细节（感兴趣的小伙伴可以在相关阅读中找到链接）。

为了将原问题转化为因果推断问题，需要设置：$Y$为销量的对数，$T$为价格的对数，$X$包括：month、DoM、DoW、stock_age_days和sku_avg_p。

$Y$和$T$需要取对数的原因是：价格和销量间的关系大致应该为
$$\tau =\frac{dQ/Q}{dP/P}$$
此处，$Q$是销量，$P$是价格。该式和DML的基本公式有些出入，需要调整一下：对上述公式两边取对数，得到
$$\log Q=\log P+截距$$
所以$Q$和$P$本身不是线性，但是取对数后，就变为线性，满足DML的使用条件了。

$X$的维度不多，如果在实际场景中，大概率还会包含商品的信息特征、用户历史购买特征等，本节的主要目标不在于精确给出其因果效应值，而是展现完整的计算过程，所以可以接受特征维度不那么全面的现状。

有了训练集后，使用因果森林DML进行训练，这个过程比较简单，一行代码便可以解决，就不赘述了。

得到模型后，依然需要使用auuc去验证模型的效果。不过在这里尤其需要注意两个方面：

(1) plot_gain和auuc_score中使用的treat只能接受0/1变量，而当前场景中价格是连续变量。代码里设置的逻辑是：$\log P$<0认为是1，反之是0，物理意义可以理解为1为降价，0为不降价。

(2) 价格和销量间的因果效应值为负数，所以在传入auuc计算时，需要先取负号，将其转为正数。

import pandas as pd
import numpy as np
from datetime import datetime, date
from causalml.metrics import plot_gain, auuc_score
from sklearn.model_selection import train_test_split
from econml.dml import CausalForestDML


def train_test_date_split():
    # 数据预处理
    df = pd.read_csv('OnlineRetail.csv', encoding="unicode_escape")
    df = df[(df['UnitPrice'] > 0) & (df['Quantity'] > 0)].reset_index(drop=True)
    df = df[~df.StockCode.isin(['POST', 'DOT', 'M', 'AMAZONFEE', 'BANK CHARGES', 'C2', 'S'])]
    df['InvoiceDate'] = pd.to_datetime(df.InvoiceDate)
    df['Date'] = pd.to_datetime(df.InvoiceDate.dt.date)
    df['revenue'] = df.Quantity * df.UnitPrice
    df = (
        df.assign(dNormalPrice=lambda d: d.UnitPrice / d.groupby('StockCode').UnitPrice.transform('median')
                  ).pipe(lambda d: d[(d['dNormalPrice'] > 1. / 3) & (d['dNormalPrice'] < 3.)]
                         ).drop(columns=['dNormalPrice'])
    )
    df = df.groupby(['Date', 'StockCode', 'Country'], as_index=False).agg({
        'Description': 'first',
        'Quantity': 'sum',
        'revenue': 'sum'
    })
    df['Description'] = df.groupby('StockCode').Description.transform('first')
    df['UnitPrice'] = df['revenue'] / df['Quantity']
    df_dml = df[(df.groupby('StockCode').UnitPrice.transform('std') > 0)]
    df_dml = df_dml.assign(
        LnP=np.log(df_dml['UnitPrice']),
        LnQ=np.log(df_dml['Quantity']),
    )
    df_dml['dLnP'] = np.log(df_dml.UnitPrice) - np.log(df_dml.groupby('StockCode').UnitPrice.transform('mean'))
    df_dml['dLnQ'] = np.log(df_dml.Quantity) - np.log(df_dml.groupby('StockCode').Quantity.transform('mean'))
    df_dml = df_dml.assign(
        month=lambda d: d.Date.dt.month,
        DoM=lambda d: d.Date.dt.day,
        DoW=lambda d: d.Date.dt.weekday,
        stock_age_days=lambda d: (d.Date - d.groupby('StockCode').Date.transform('min')).dt.days,
        sku_avg_p=lambda d: d.groupby('StockCode').UnitPrice.transform('median')
    )
    
    y = df_dml['dLnQ']
    treat = df_dml['dLnP']
    X = df_dml[['month', 'DoM', 'DoW', 'stock_age_days', 'sku_avg_p']]

    y_train, y_test, treat_train, treat_test, X_train, X_test = train_test_split(y, treat, X, test_size=.2)

    return X_train, y_train, treat_train, X_test, y_test, treat_test


if __name__ == '__main__':
    # 整合训练和测试数据
    X_train, y_train, treat_train, X_test, y_test, treat_test = train_test_date_split()

    # 因果森林DML训练
    cf_dml = CausalForestDML(n_jobs=1).fit(y_train, treat_train, X=X_train)

    # AUUC评估训练集效果
    train_df = pd.DataFrame({
        'y': y_train,
        'treat': np.where(treat_train.values < 0, 1, 0),
        'cf_dml': -cf_dml.effect(X_train)
    })
    plot_gain(train_df, outcome_col='y', treatment_col='treat', normalize=True, random_seed=10, n=100, figsize=(8, 8))
    auuc = auuc_score(train_df, outcome_col='y', treatment_col='treat', normalize=True, tmle=False)
    print('train set auuc:')
    print(auuc)

    # AUUC评估测试集效果
    test_df = pd.DataFrame({
        'y': y_test,
        'treat': np.where(treat_test.values < 0, 1, 0),
        'cf_dml': -cf_dml.effect(X_test)
    })
    plot_gain(test_df, outcome_col='y', treatment_col='treat', normalize=True, random_seed=10, n=100, figsize=(8, 8))
    auuc = auuc_score(test_df, outcome_col='y', treatment_col='treat', normalize=True, tmle=False)
    print('\ntest set auuc:')
    print(auuc)

以下是代码的输出结果。从结果上来看，模型的auuc优于随机排序的auuc，同时测试集的auuc略低于训练集的auuc，整体上来看是符合预期的。

train set auuc:
cf_dml    0.691234
Random    0.500072
dtype: float64

test set auuc:
cf_dml    0.623231
Random    0.499888
dtype: float64

4 总结

文章正文到此就结束了，本节总结一下三个比较重要的内容：

(1) DML的原理是：基于对结果变量和策略变量残差的拟合，可以得到真正的因果效应值。

(2) econml工具包可以调用DML和因果森林DML算法。

(3) 使用auuc评估DML的预测效果时，可以调用causalml工具包。

5 相关阅读

DML算法原文：https://academic.oup.com/ectj/article/21/1/C1/5056401?login=false

DML算法原理讲解1：https://academic.oup.com/ectj/article/21/1/C1/5056401?login=false

DML算法原理讲解2：https://blog.csdn.net/a358463121/article/details/123999934

DML实例1：https://cloud.tencent.com/developer/article/1913864

DML实例2：https://cloud.tencent.com/developer/article/1938132

FWL定理：https://www.bilibili.com/video/BV1dA411H7nP/?spm_id_from=333.788&vd_source=f416a5e7c4817e8efccf51f2c8a2c704

在线零售销售数据：https://www.kaggle.com/datasets/vijayuv/onlineretail

销售数据预处理：https://github.com/Serena-TT/36-methods-for-data-analysis/blob/main/DML.ipynb

原文地址：https://blog.csdn.net/taozibaby/article/details/140591792

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！