算法日记day 16（二叉树的广度优先遍历|反转、对称二叉树）

🕗 发布于 2024-07-21 21:41 算法宽度优先 数据结构 java

一、二叉树的层序遍历

题目：

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

示例 1：

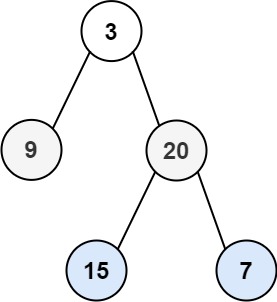
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

思路：

用队列来存储元素，变量size来存储每一层的元素个数，扫描队头元素，判断其是否有左右孩子，如果有，将其入队，同时该队头元素出队，记录在该层所封装的结果集中，同时size减一，当size值减为0时，说明该层所有元素均遍历完毕，返回结果集

代码：

// 结果列表，用于存储每一层的节点值列表
public List<List<Integer>> resList = new ArrayList<List<Integer>>();

// 主方法，进行二叉树的层次遍历
public List<List<Integer>> levelOrder(TreeNode root) {
    // 调用辅助方法进行层次遍历
    test(root);
    // 返回结果列表
    return resList;
}

// 辅助方法，实现二叉树的层次遍历
public void test(TreeNode root) {
    // 如果根节点为空，直接返回
    if (root == null)
        return;

    // 创建队列，用于存储待处理的节点
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root); // 将根节点加入队列

    // 循环处理队列中的节点，直到队列为空
    while (!queue.isEmpty()) {
        // 用于存储当前层节点值的列表
        List<Integer> list = new LinkedList<>();
        int len = queue.size(); // 当前层节点的数量

        // 处理当前层的所有节点
        while (len > 0) {
            TreeNode tnode = queue.poll(); // 出队列，获取当前处理的节点
            list.add(tnode.val); // 将节点值加入当前层的列表

            // 将当前节点的左右子节点加入队列，用于下一层处理
            if (tnode.left != null)
                queue.add(tnode.left);
            if (tnode.right != null)
                queue.add(tnode.right);

            len--; // 当前层节点数减一
        }

        // 将当前层的节点值列表加入结果列表
        resList.add(list);
    }
}

resList 定义和初始化：
- public List<List<Integer>> resList = new ArrayList<List<Integer>>();
- 定义了一个成员变量 resList，用于存储二叉树的层次遍历结果。初始化为空的 ArrayList，用于存储每一层的节点值列表。
levelOrder 方法：
- public List<List<Integer>> levelOrder(TreeNode root)
- 主方法，调用 test 方法进行二叉树的层次遍历，并返回最终的层次遍历结果 resList。
test 方法：
- public void test(TreeNode root)
- 辅助方法，实现二叉树的层次遍历。
- 使用队列 queue 进行广度优先搜索（BFS）：
  - 首先将根节点加入队列。
  - 每次处理队列中的一个节点，将其值加入当前层的 list 中，并将其左右子节点（如果存在）加入队列。
  - 每处理完一层的所有节点后，将当前层的节点值列表 list 加入 resList 中。

二、翻转二叉树

题目：

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

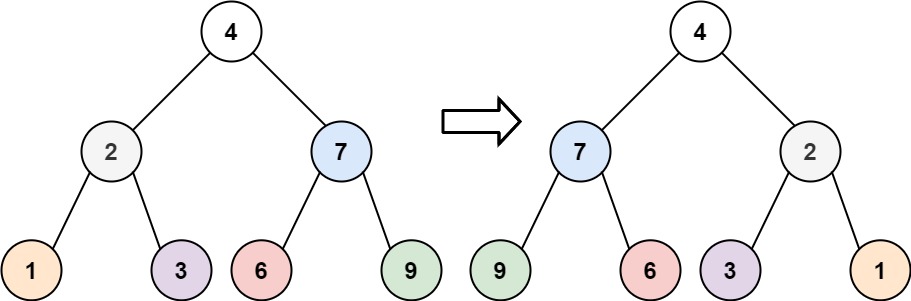
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

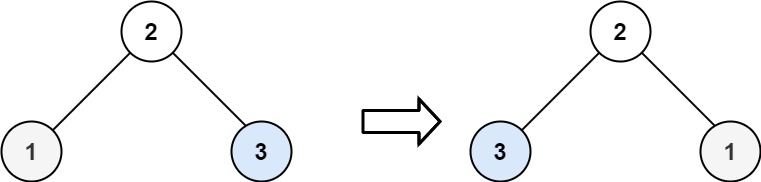
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

思路：

可以采用递归前序和后序遍历的方法，遍历一个结点的同时反转其左右子节点，接着往下一层移动，重复以上操作，直到遍历到的节点为空停止

代码：

//前序
public TreeNode invertTree(TreeNode root) {
    if (root == null)
        return root;
    swap(root); // 调用 swap 方法，交换当前节点的左右子节点  中
    invertTree(root.left); // 递归翻转左子树   左
    invertTree(root.right); // 递归翻转右子树   右
    return root; // 返回翻转后的根节点
}
public void swap(TreeNode root) {
    TreeNode temp = root.left;
    root.left = root.right;
    root.right = temp;
}

后序遍历方法类似，只需将顺序修改为左，右，中即可

用中序遍历的方法稍有不同，由于中序是左，中，右的顺序，当返回到根节点时左右子树交换顺序，此时应该继续遍历右子树，但是这时的右子树正好是刚刚交换完的左子树 ，因此实际上仅是交换了一次左子树，要想实现反转，必须再次进行左子树的交换操作即可，代码如下：

invertTree(root.left); // 递归翻转左子树   左
swap(root); // 调用 swap 方法，交换当前节点的左右子节点  中
invertTree(root.left); // 这时再次操作反转后的左子树   右

三、对称二叉树

题目：

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

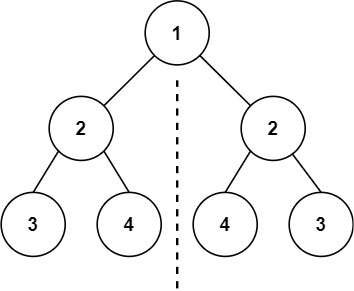
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

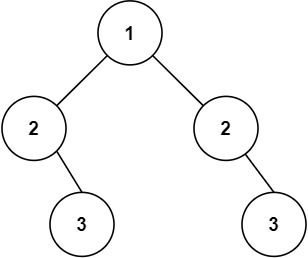
输入：root = [1,2,2,null,3,null,3]
输出：false

思路：

采用后序遍历的方法，为什么要采用后序呢？由于后序遍历的顺序是左，右，中，而要判断二叉树是否对称就是要判断根节点的左右子树是否在翻转后可以重合，后序的遍历顺序正好可以判断左右子树，再在最后遍历根节点，具体方法是，先遍历根节点的左右子节点是否相同，再判断左子节点的左子节点是否与右子节点的右子节点相同，同理再判断左子节点的右子节点是否和右子节点的左子节点相同，重复上述操作，直到为空

代码：

// 判断给定的二叉树是否对称的方法
public boolean isSymmetric(TreeNode root) {
    // 调用 compare 方法，比较根节点的左右子树是否对称
    return compare(root.left, root.right);
}

// 递归比较两棵树是否对称的方法
public boolean compare(TreeNode left, TreeNode right) {
    // 边界情况处理：
    // 左子树不为空而右子树为空，或者左子树为空而右子树不为空，二叉树不对称，返回 false
    if (left != null && right == null)
        return false;
    if (left == null && right != null)
        return false;
    
    // 左右子树都为空，认为对称，返回 true
    if (left == null && right == null)
        return true;
    
    // 比较当前节点值是否相等，若不相等，二叉树不对称，返回 false
    if (left.val != right.val)
        return false;
    
    // 递归比较左子树的左节点与右子树的右节点，外侧比较
    boolean Outcompare = compare(left.left, right.right);
    // 递归比较左子树的右节点与右子树的左节点，内侧比较
    boolean Intcompare = compare(left.right, right.left);
    
    // 返回外侧比较和内侧比较的与运算结果，确定整棵树是否对称
    return Outcompare && Intcompare;
}

首先处理边界情况：
- 如果 left 不为 null 而 right 为 null，或者 left 为 null 而 right 不为 null，则二叉树不对称，返回 false。
- 如果 left 和 right 都为 null，则认为是对称的，返回 true。
然后比较当前节点的值 left.val 和 right.val 是否相等，如果不相等，则二叉树不对称，返回 false。
如果当前节点值相等，继续递归比较 left 的左子节点 left.left 和 right 的右子节点 right.right 是否对称（外侧比较）。
同时递归比较 left 的右子节点 left.right 和 right 的左子节点 right.left 是否对称（内侧比较）。
最终返回外侧比较结果 Outcompare 和内侧比较结果 Intcompare 的与运算结果，即判断整棵树是否对称。

算法日记day 16（二叉树的广度优先遍历|反转、对称二叉树）

一、二叉树的层序遍历

二、翻转二叉树

三、对称二叉树

相关文章