机器学习系列6-逻辑回归
| 重点: 1.逻辑回归模型会生成概率。 2. 对数损失是逻辑回归的损失函数。 3. 逻辑回归被许多从业者广泛使用。 |
在许多情况下,您需要将逻辑回归输出映射到二元分类问题,其中目标是正确预测两个可能的标签之一(例如,“垃圾邮件”或“不是垃圾邮件”)。后续模块会重点介绍这一点。
您可能想知道逻辑回归模型如何确保输出值始终介于 0 和 1 之间。巧合的是,S 型函数会产生如下具有相同特征的输出(定义如下):

S 型函数生成以下图表:
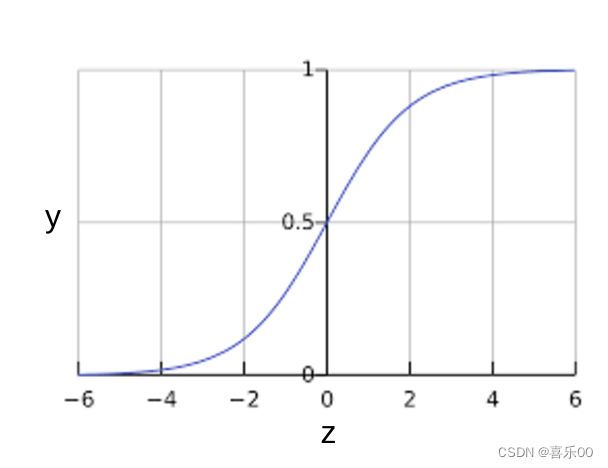

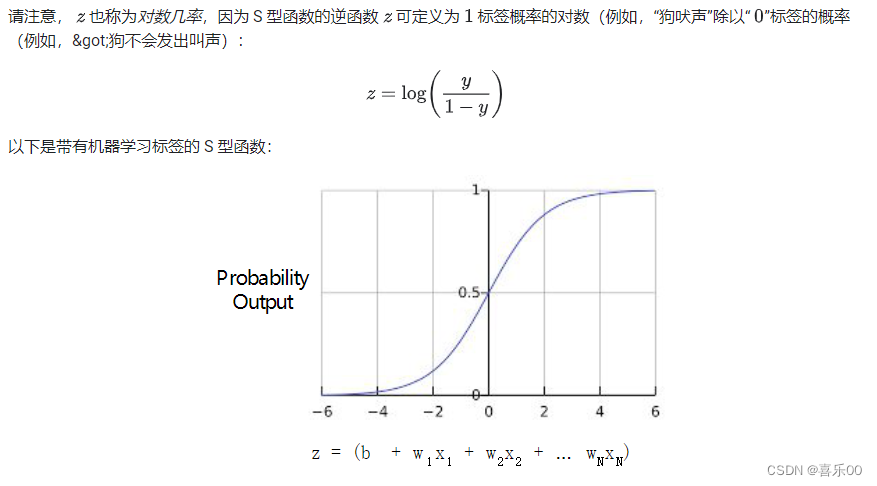
逻辑回归推断计算。

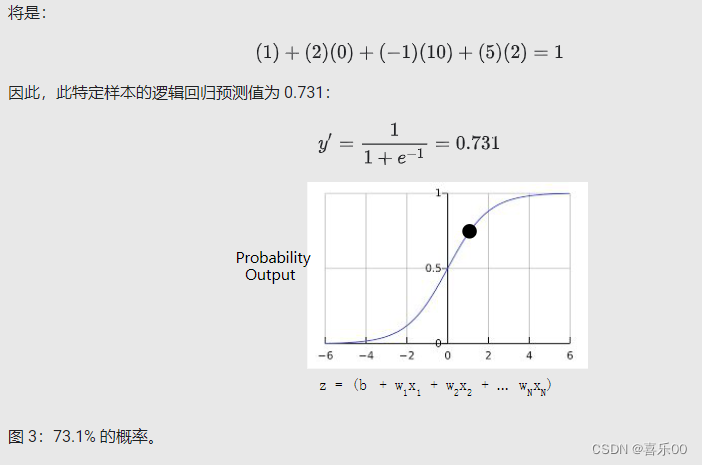
2.逻辑回归:损失和正则化
2.1.逻辑回归的损失函数
线性回归的损失函数是平方损失。逻辑回归的损失函数是对数损失,定义如下:

2.2.逻辑回归中的正则化
正则化在逻辑回归建模中极其重要。 如果不进行正则化,高逻辑维度下的逻辑回归的渐近性会不断促使损失接近 0。因此,大多数逻辑回归模型都使用以下两种策略之一来降低模型复杂性:
- L2 正则化。
- 早停法,即限制训练步数或学习速率。
假设您为每个示例分配一个唯一 ID,并将每个 ID 映射到其自己的特征。如果您不指定正则化函数,模型将完全过拟合。这是因为模型会尝试在所有样本上将损失降低为零,并且永远无法实现,从而将每个指示器特征的权重提高至 +无穷大或-无穷大。当有大量罕见的交叉时,仅在一个样本上发生,就会出现包含特征组合的高维度数据。
幸运的是,使用 L2 或早停法可以防止此问题出现。
原文地址:https://blog.csdn.net/weixin_38457055/article/details/136043087
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
