【强化学习入门笔记】1.1基本概念
本系列为学习赵世钰老师的《强化学习的数学原理》所作的学习笔记.
**课程视频网址:**https://space.bilibili.com/2044042934

1.1.1 网格世界示例
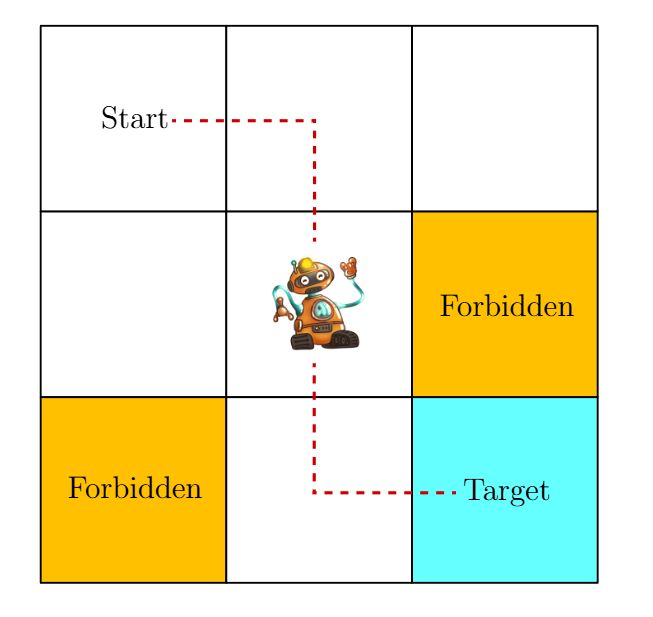
首先给出了课程中需要用的模拟场景: 一个有边界的网格世界. 由起点, 终点和禁止网格. 目的是得到一条从起点到终点的最优路径.
1.1.2 State, Action, Policy 状态, 动作, 策略
1.1.2.1 状态和状态空间
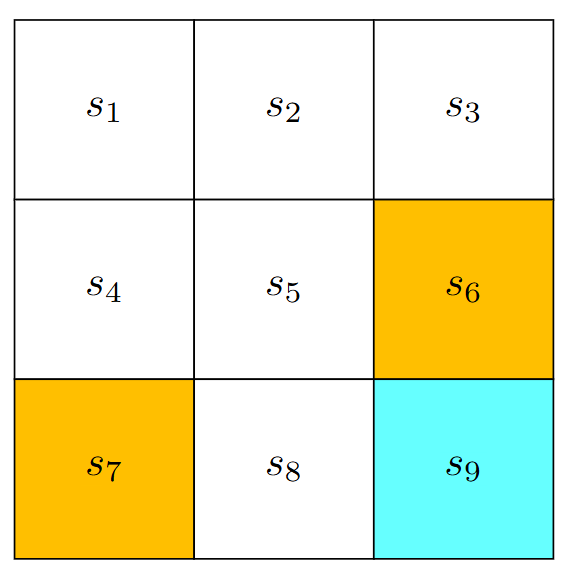
在网格世界示例中, 我们将状态定义为栅格的索引 s 1 , … , s 9 s_1, \ldots, s_9 s1,…,s9. 实际上, 更复杂的建模状态中可以包含:速度, 加速度, 角速度等等信息.
将一系列状态放进一个集合中称之为状态空间 S = { s 1 , … , s 9 } \mathcal{S}=\left\{s_1, \ldots, s_9\right\} S={s1,…,s9}
1.1.2.2 动作和动作空间
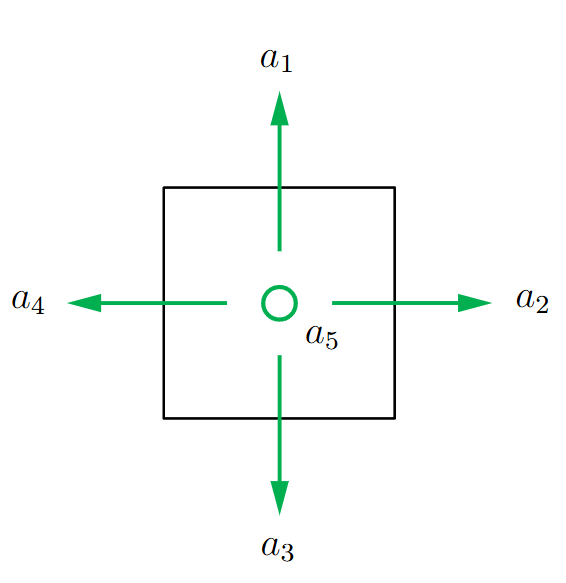
如上图所示, 我们将动作定义为:向上走 a 1 a_1 a1, 向右走 a 2 a_2 a2等等. 将一系列动作放进一个集合中称之为动作空间 A = { a 1 , … , a 5 } \mathcal{A}=\left\{a_1, \ldots, a_5\right\} A={a1,…,a5}
每一个状态都有对应的动作空间, 比如对于左上角栅格状态 s 1 s_1 s1, 它能采取的动作只有向右, 向下和不动. 因此它的动作空间为: A ( s 1 ) = { a 2 , a 3 , a 5 } \mathcal{A}\left(s_1\right)=\left\{a_2, a_3, a_5\right\} A(s1)={a2,a3,a5}
也就是说, 动作空间是一个关于状态空间的函数:
A ( s i ) = A = { a 1 , … , a 5 } \mathcal{A}\left(s_i\right)=\mathcal{A}=\left\{a_1, \ldots, a_5\right\} A(si)=A={a1,…,a5}
1.1.2.3 状态转移
从 s 1 s_1 s1执行向右的动作到 s 2 s_2 s2, 可以写作: s 1 → a 2 s 2 . s_1 \xrightarrow{a_2} s_2 . s1a2s2.
一般的, 采取动作从一个状态转移到另一个状态的过程, 定义为状态转移:
s i → a j s k . s_i \xrightarrow{a_j} s_k . siajsk.
我们列举出了网格世界示例中, 所有的状态转移组合:

如果我们用条件概率来表达状态转移:
p ( s 1 ∣ s 1 , a 2 ) = 0 , p ( s 2 ∣ s 1 , a 2 ) = 1 , p ( s 3 ∣ s 1 , a 2 ) = 0 , p ( s 4 ∣ s 1 , a 2 ) = 0 , p ( s 5 ∣ s 1 , a 2 ) = 0 , \begin{aligned}& p\left(s_1 \mid s_1, a_2\right)=0, \\& p\left(s_2 \mid s_1, a_2\right)=1, \\& p\left(s_3 \mid s_1, a_2\right)=0, \\& p\left(s_4 \mid s_1, a_2\right)=0, \\& p\left(s_5 \mid s_1, a_2\right)=0,\end{aligned} p(s1∣s1,a2)=0,p(s2∣s1,a2)=1,p(s3∣s1,a2)=0,p(s4∣s1,a2)=0,p(s5∣s1,a2)=0,
1.1.2.4 Policy 策略
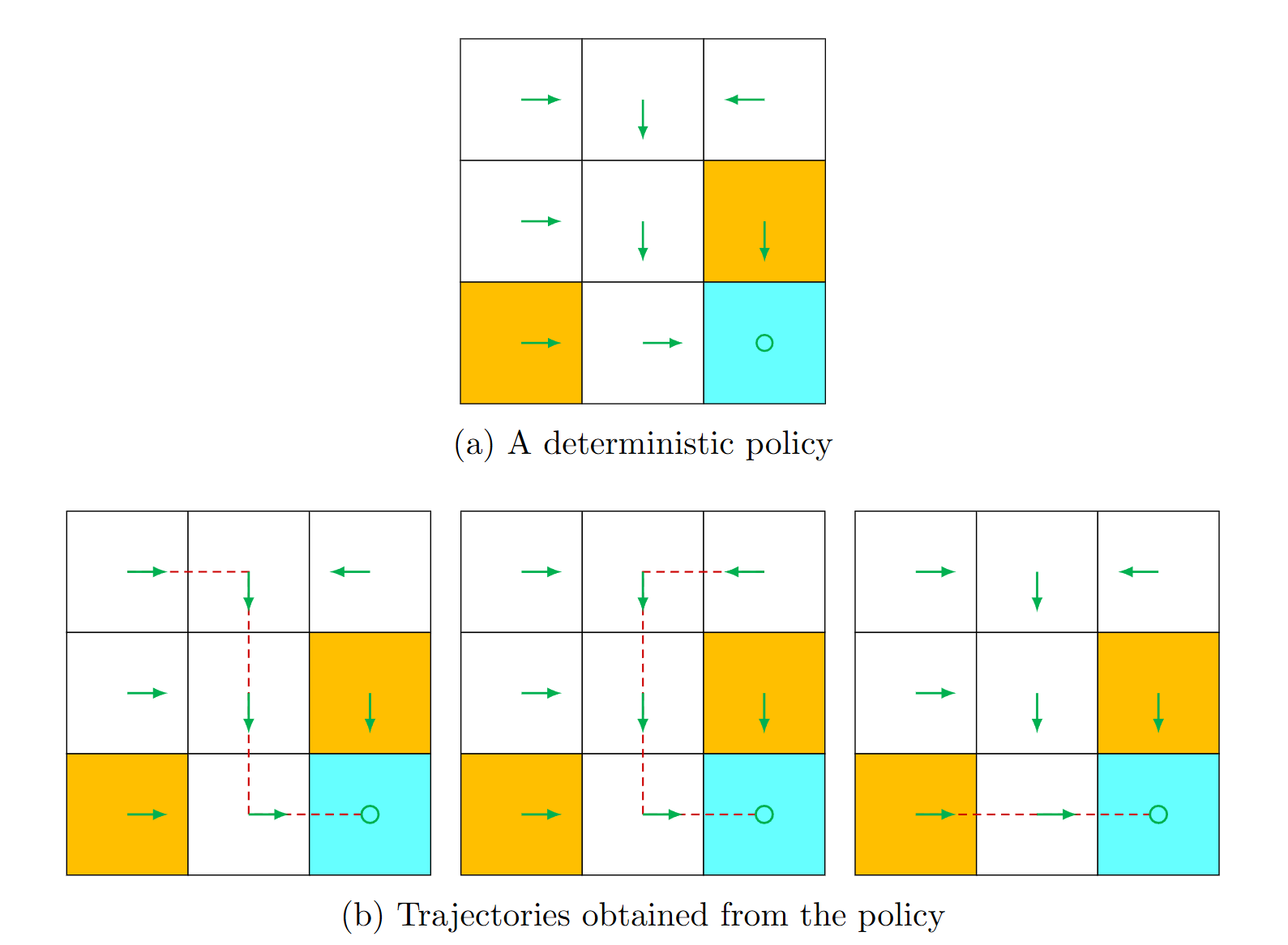
策略是指对于每一个状态而言, 为了抵达目的应该采取的动作称之为策略. 比如上图给出了在不同状态下, 绿色箭头就是对应的策略.
我们将策略定义为 π ( a ∣ s ) \pi(a \mid s) π(a∣s), 也就是当状态为 s s s时采取动作 a a a的概率, 上图的策略可以写成:
π ( a 1 ∣ s 1 ) = 0 π ( a 2 ∣ s 1 ) = 1 π ( a 3 ∣ s 1 ) = 0 π ( a 4 ∣ s 1 ) = 0 π ( a 5 ∣ s 1 ) = 0 \begin{aligned}& \pi\left(a_1 \mid s_1\right)=0 \\& \pi\left(a_2 \mid s_1\right)=1 \\& \pi\left(a_3 \mid s_1\right)=0 \\& \pi\left(a_4 \mid s_1\right)=0 \\& \pi\left(a_5 \mid s_1\right)=0\end{aligned} π(a1∣s1)=0π(a2∣s1)=1π(a3∣s1)=0π(a4∣s1)=0π(a5∣s1)=0
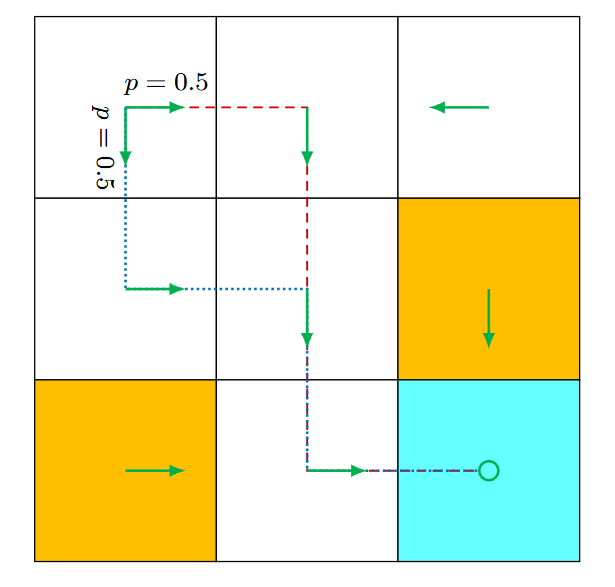
如上图, 如果策略可以按概率采取不同的动作, 则可以写成:
π ( a 2 ∣ s 1 ) = 0.5 π ( a 3 ∣ s 1 ) = 0.5 \begin{aligned}& \pi\left(a_2 \mid s_1\right)=0.5 \\& \pi\left(a_3 \mid s_1\right)=0.5\end{aligned} π(a2∣s1)=0.5π(a3∣s1)=0.5
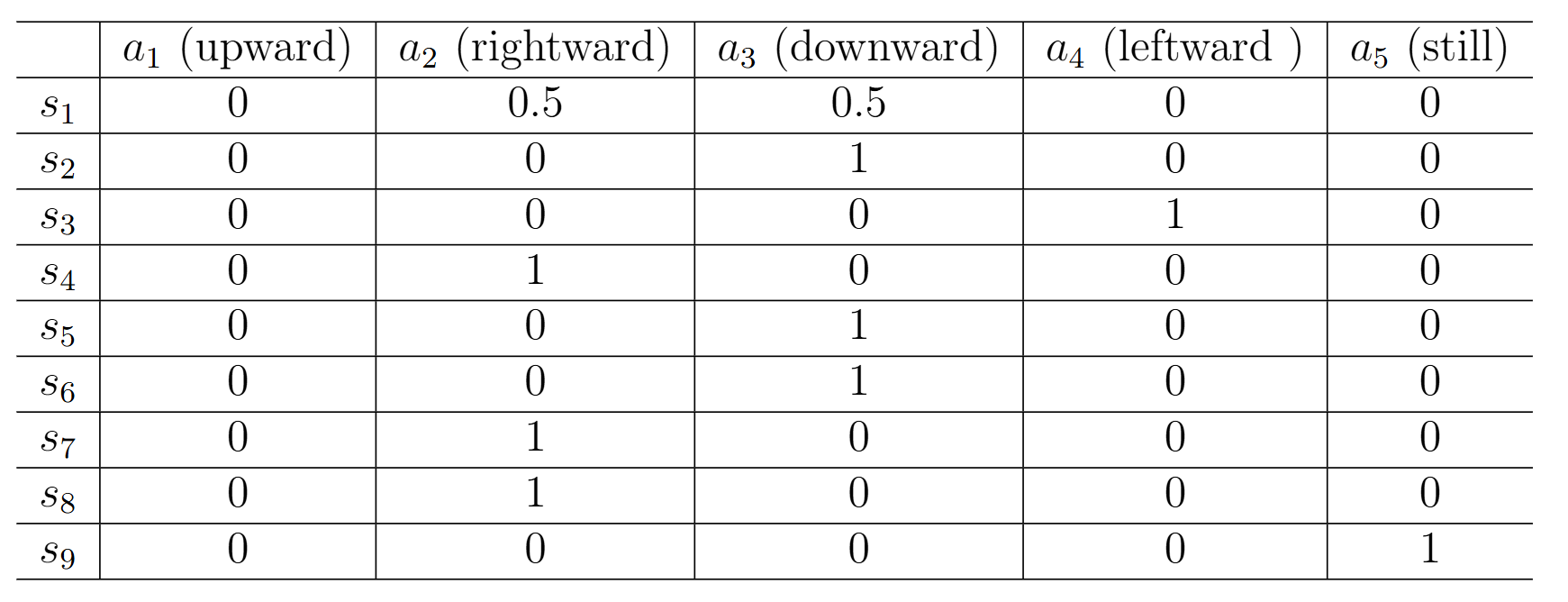
在程序中, 我们常常使用一个矩阵来表达完整的策略分布:
1.1.3 Reward, Return
1.1.3.1 Reward 奖励
Reward是指采取动作之后, 得到的奖励值, 是一个标量. 奖励值越高, 采取的动作越受鼓励, 因此我们需要设计合适的Reward 函数来鼓励智能体采取我们希望的动作.
我们将处于状态s, 执行动作a, 奖励函数定义为: r ( s , a ) r(s, a) r(s,a)
以网格世界为例, 我们可以设计如下奖励:
- 如果智能体越过边界, 或者走到禁止网格, 则奖励值为-1
- 如果智能体抵达目的, 则奖励值为1
- 其他情况, 奖励值为0
所以可以写出: r ( s 1 , a 1 ) = − 1 r(s_1, a_1)=-1 r(s1,a1)=−1, r ( s 5 , a 2 ) = − 1 r(s_5, a_2)=-1 r(s5,a2)=−1, r ( s 8 , a 2 ) = 1 r(s_8, a_2)=1 r(s8,a2)=1
1.1.3.2 Trajectories, returns
我们将一组连续的状态定义为Trajectory, 每一个状态都从上一个状态采取动作转移而来. 每次状态转移都有对应的奖励.
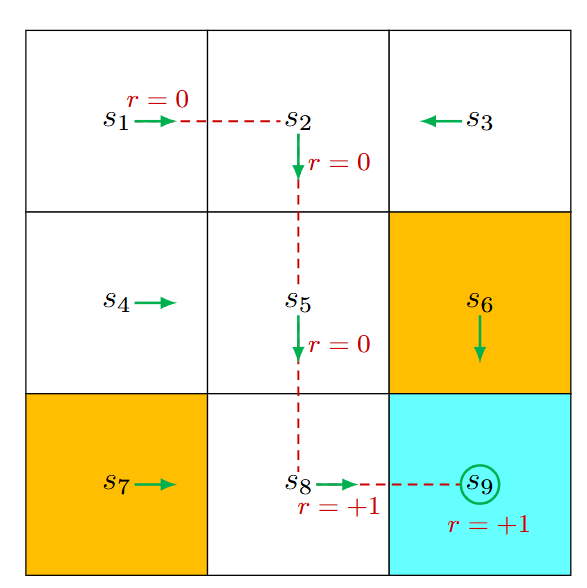
上图的trajectory可以写成:
s 1 → r = 0 a 2 s 2 → r = 0 a 3 s 5 → r = 0 a 3 s 8 → r = 1 a 2 s 9 . s_1 \xrightarrow[r=0]{a_2} s_2 \xrightarrow[r=0]{a_3} s_5 \xrightarrow[r=0]{a_3} s_8 \xrightarrow[r=1]{a_2} s_9 . s1a2r=0s2a3r=0s5a3r=0s8a2r=1s9.
将trajectory上每一步的奖励加起来, 定义为return:
return = 0 + 0 + 0 + 1 = 1 \text { return }=0+0+0+1=1 return =0+0+0+1=1
如果我们在抵达终点之后, 没有中止游戏. 那么奖励值就会不停的+1导致发散:
return = 0 + 0 + 0 + 1 + 1 + 1 + ⋯ = ∞ \text { return }=0+0+0+1+1+1+\cdots=\infty return =0+0+0+1+1+1+⋯=∞
为了解决这个问题, 可以采取discounted return, 也就是奖励值的加权和:
discounted return = 0 + γ 0 + γ 2 0 + γ 3 1 + γ 4 1 + γ 5 1 + … = γ 3 ( 1 + γ + γ 2 + … ) = γ 3 1 1 − γ . \begin{aligned}\text { discounted return } & =0+\gamma 0+\gamma^2 0+\gamma^3 1+\gamma^4 1+\gamma^5 1+\ldots \\ & =\gamma^3\left(1+\gamma+\gamma^2+\ldots\right)=\gamma^3 \frac{1}{1-\gamma} . \end{aligned} discounted return =0+γ0+γ20+γ31+γ41+γ51+…=γ3(1+γ+γ2+…)=γ31−γ1.
其中 γ \gamma γ是远期奖励值的权重. 这样可以增加近期动作获得奖励的权重, 减少远期动作获得奖励的权重.

原文地址:https://blog.csdn.net/2403_86993842/article/details/143494784
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
