微分几何-曲线论（曲线）

曲线

定义

称三维欧氏空间$R$中的向量函数$\mathbf{r}(t)=x(t),y(t),z(t),t\in (a,b)$为一条空间参数曲线，简称曲线，我们也把函数的自变量$t$称为是曲线的参数.

注：由于向量函数的终点位置和$x(t),y(t),z(t)$是一一对应的，因此可以将向量函数表示的空间曲线看作空间质点随$t$变动的轨迹。这时，曲线也是有方向的. 我们规定随着参数$t$的增加，曲线上点的运动方向为曲线的正向.

常见曲线

直线

直线的向量函数一般形式为$\mathbf{r}(t)=\mathbf{a}t+\mathbf{b}$，表示过定点$\mathbf{b}$，方向向量为$\mathbf{a}$的直线.

如 r ( t ) = { t , t , t } , t ∈ R \boldsymbol{r}(t)=\{t, t, t\}, t \in \mathbb{R} r(t)={t,t,t},t∈R表示过定点$(0,0,0)$，方向为$(1,1,1)$的一条直线.

在这里补充解析几何中直线方程的几种形式：

• 一般形式（通过两平面相交只有一条交线，联立方程组即为一般形式）
• 点向式（已知直线过一点和直线的方向向量）
• 参数式（很容易由点向式导出直线的参数方程形式）

圆

曲线$C$： r ( t ) = { cos ⁡ t , sin ⁡ t , 0 } , t ∈ R \boldsymbol{r}(t)=\{\cos t, \sin t, 0\}, t \in \mathbb{R} r(t)={cost,sint,0},t∈R是$xOy$平面上的单位圆，方向为逆时针方向.

圆柱螺线

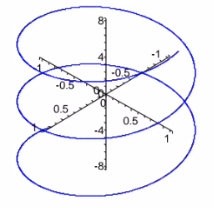
曲线$C$： r ( t ) = { cos ⁡ t , sin ⁡ t , t } , t ∈ R \boldsymbol{r}(t)=\{\cos t, \sin t, t\}, t \in \mathbb{R} r(t)={cost,sint,t},t∈R表示圆柱螺线，其方向从下到上. 圆柱螺线既是是光滑曲线，也是正则曲线.

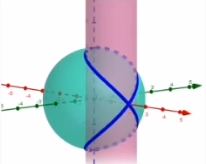
维维安尼曲线

该曲线是由一个半径为$a$的球面与一个经过球面的一条直径，且半径为$a/2$的圆柱面相交而成的空间曲线.

曲线$C$：$\mathbf{r}(t)=\left\{1+\cos t,\sin t,2\sin \frac{t}{2}\right\},t\in (-2\pi ,2\pi )$是正则曲线.

连续曲线/光滑曲线

如果向量函数是$C^n$类的，即向量函数具有连续的$n$阶导数，则称对应的曲线为$C^n$类曲线. 特别地，$C^0$类曲线称为连续曲线，$C^1$类曲线称为光滑曲线，向量函数具有任意阶导数的曲线叫做$C^{\infty }$类曲线.

正则曲线

设空间曲线$C$：$\mathbf{r}=\mathbf{r}(t)$是至少$C^1$类的，如果在$t_0$处有${\mathbf{r}}^{\prime }(t_0)\ne 0$，则称曲线在$t_0$处正则，点$\mathbf{r}(t_0)$称为曲线的正则点（或正常点）; 否则称曲线在$t_0$处非正则，点$\mathbf{r}(t_0)$称为曲线$C$的奇异点. 如果曲线上的每一点都是曲线的正则点，则称该曲线是正则曲线.

**注：**在后续章节中，如果不作特殊说明，我们约定研究的曲线均为至少$C^3$类正则空间曲线. 曲线$C$：$\mathbf{r}=\mathbf{r}(t)$在$t_0$处正则当且仅当$\left|{\mathbf{r}}^{\prime }\left(t_0\right)\right|\ne 0$. 需要曲线的正则性与其是否连续光滑没有直接关系. 如半立方抛物线$\mathbf{r}(t)=\left\{t^3,t^2,0\right\}$是$C^{\infty }$类曲线，但不是正则曲线.

半立方抛物线

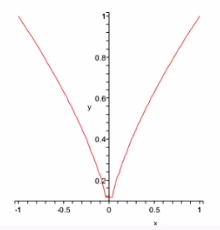
注：对于曲线光滑性的要求，就是要排除曲线上比较“尖锐”的点：而正则性的要求，就是排除能够通过光滑性的要求，但是切向量变化不连续的特殊点（比如带尖点的曲线），即便这 个点两侧曲线都是平滑过渡的.

切向量

要给出切向量的概念，我们首先考虑切线是如何形成的.

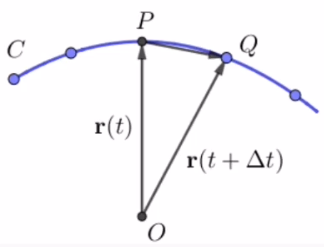
给出曲线上一点$P$，点$Q$是$P$的邻近一点，如图.

把割线$PQ$绕$P$点旋转，使$Q$点沿曲线趋近于$P$点. 若割线$PQ$趋于一固定的位置，则我们把这个割线$PQ$的极限位置称为曲线在$P$点的切线. 而定点$P$称为切点.

直观上看，切线是通过切点的所有直线中最贴近曲线的直线.

下面我们通过切线的定义引入切向量的概念，首先设曲线的向量函数为$\mathbf{r}=\mathbf{r}(t)$，切点$P$对应参数$t_0$，$Q$点对应参数$t_0+\Delta t$，如图.

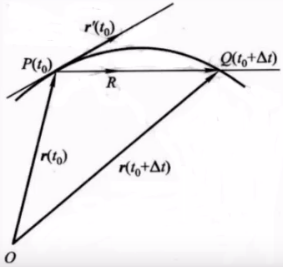
注：当曲线是正则曲线时，曲线上的每一点都是正常点（${\mathbf{r}}^{\prime }(t_0)\ne 0$），因此曲线在每一点的存在非零切向量. 而这个切向量就是切线上的一个非零向量，因而就是切线的一个方向向量. 由以上的推导过程可以看出，这个切向量的正向和曲线的参数$t$的增量方向是一致的.

切线方程

由切点和切向量很容易得到切线方程.

注意直线方程的分母只要不全为0就是有意义的.

法平面（法面）

经过切点而垂直于切线的平面称为曲线的法平面或法面.

一个平面可由一个定点以及平面的一个法向量唯一确定，由于定点和法向量，也就是切向量都是已知的，所以也很容易写出法平面的点法式方程.

弧长

对曲线的正则性要求，保证了曲线在每一点都存在切向量，由数学分析的知识可知，这还保证了曲线是可求长的.

以下依然利用微积分的知识，通过将曲线微分成无限多的小段推导弧长公式.

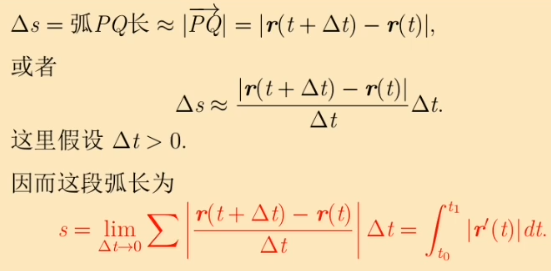
定理1：弧长公式

曲线$C$：$\mathbf{r}=\mathbf{r}(t),t\in (t_0,t_1)$的弧长为：
$$s={\int }_{t_0}^{t_1}\left|{\mathbf{r}}^{\prime }(t)\right|dt$$
注：在弧长公式中，令$t_1=t$，则可以得到
$$s={\int }_{t_0}^t\left|{\mathbf{r}}^{\prime }(t)\right|dt$$
这样我们可以将弧长理解为一个关于变量$t$的实函数.

弧长参数化

考虑圆从$0$到$t$的弧长.

考虑圆柱螺线从$0$到$t$的弧长.

这两个例子表明利用弧长公式，我们可以将一般参数表示的向量函数“转化”为弧长参数表示的向量函数. 我们将这件事情称为弧长参数化. 事实上，从理论上看，任何一条正则曲线都可以弧长参数化.

定理2：任何一条正则曲线都可以使用弧长作参数.（也称弧长参数为自然参数）

**证明：**利用变上限函数导数公式以及单调函数存在反函数.

**注：**利用弧长公式，我们可以得到以下两个非常常用的式子
$$\frac{ds}{dt}=\left|{\mathbf{r}}^{\prime }(t)\right|\text{ 或 }\frac{dt}{ds}=\frac{1}{\left|{\mathbf{r}}^{\prime }(t)\right|}$$
后面我们会逐渐发现弧长参数化对于研究曲线的便捷之处.

定理3（弧长表示的向量函数一阶导数以及二阶导数的性质）

若曲线$C$：$\mathbf{r}=\mathbf{r}(s)$的参数为弧长

则$\left|{\mathbf{r}}^{\prime }(s)\right|\equiv 1$，且${\mathbf{r}}^{\prime }(s)$与${\mathbf{r}}^{\prime \prime }(s)$处处垂直.

此时称${\mathbf{r}}^{\prime }(s)$为曲线$C$的单位切向量，也记为$\mathbf{\alpha }(s)$

**证明：**利用了上一节的定理，向量函数有固定长当且仅当其一阶导和二阶导的点积为0.

最后补充一个结论：所有切线过定点的曲线是直线.

原文地址：https://blog.csdn.net/qq_45607390/article/details/143029556

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！