LeetCode 73.矩阵置零————2024 春招冲刺百题计划

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

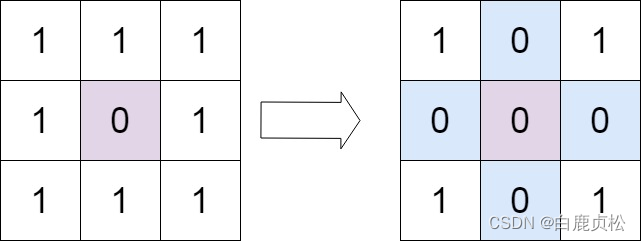
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]
示例 2：

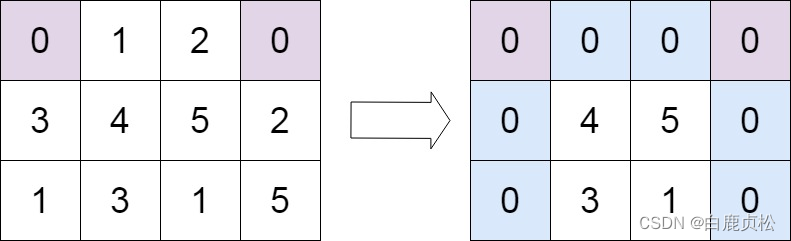
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
思路
方法一：遍历一遍，使用俩set分别存储存在空值的行和列，空间复杂度：O(m+n)
方法二：使用两个标记变量分别记录第一行和第一列是否原本包含 0，用矩阵的第一行和第一列代替方法一中的两个标记数组，以达到 O(1)
方法三：使用一个标记变量记录第一列，而第一列的第一个元素标记第一行，为了防止每一列的第一个元素被提前更新，我们需要从最后一行开始，倒序地处理矩阵元素。
方法一代码

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        set<int> s,s1;
        int m = matrix.size();
        int n = matrix[0].size();
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(!matrix[i][j]){
                    s.insert(i);
                    s1.insert(j);
                }
            }
        }
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(s.find(i) != s.end()||s1.find(j) != s1.end())
                    matrix[i][j]=0;
            }
        }

    }
};

方法二代码

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        bool flag1 = false, flag2 = false;
        for(int i = 0; i < m; i++){
            if(!matrix[i][0]) flag1 = true;
        }
        for(int i = 0; i < n; i++){
            if(!matrix[0][i]) flag2 = true;
        }
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(!matrix[i][j]){
                    matrix[i][0] = matrix[0][j] = 0;
                } 
            }
        }
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                if(!matrix[i][0]||!matrix[0][j]){
                    matrix[i][j] = 0;
                }
            }
        }
        if(flag1){
            for(int i = 0; i < m; i++) matrix[i][0] = 0;
        }
        if(flag2){
            for(int i = 0; i < n; i++) matrix[0][i] = 0;
        }
    }
};

原文地址：https://blog.csdn.net/m0_46314779/article/details/137573370

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！