基于KNN的旋转机械故障诊断Matlab实现

KNN算法又称K-近邻算法，其主要思想是对于要分类的样本按照一定的相似性度量方法寻找与之最近的K个邻居，计算这K个邻居中类别出现次数最多的那个类作为该样本所属类。其算法步骤如下：

(1) 计算待分类样本与训练集中各个数据之间的距离；

(2) 将计算出的距离按照升序进行排列；

(3) 选取顺序当中的前 K 个训练样本，作为该待分类样本的 K 个邻居；

(4) 统计上一步选出的 K 个邻居出现的类别频率；

(5) 将出现频率最高的类别作为待分类样本所属的类。

KNN 模型使用时不需要前期进行模型训练，结构较为简单易于理解，精度相对来说比较高，并且对异常值不是很敏感。KNN 模型的缺点在于样本不均衡问题，即如果出现在训练集中某些样本占比较大，那么将会导致 KNN 模型在分类时更偏向于将待分类样本分到该类中。并且 KNN算法还有一个缺点就是模型在对 K 值的设定上比较敏感，需要提前进行模型 K 值的设定，不同的 K 值将会对分类结果有直接的影响。

在文本分类领域有很多应用比较广泛的模型，例如决策树，支持向量机等等，当然像决策树这样的模型与 KNN 模型相比来说其规则比较简单，但他们只适用于较小尺寸的文档，而 KNN 模型对于较大尺寸的文档也有很好的分类效果。KNN 模型在文本分类领域有很广泛的应用，除了利用提取一些文本的特征进行传统意义上的分类，也有其一些 KNN 的相关变形应用到文本分类领域。在图像分类领域 KNN 利用其模型实现简单，理论清晰，分类时不需要先验知识的特点得到了广泛应用。在图像分类问题上一般采用提取图像的一些特征值比如针对图像的灰度矩阵进行特征提取，或者进行图像分割。

KNN模型在多数情况下是用在分类问题上，在预测问题上也有相关应用。试想在做分类过程中确定类别时是利用与待分类样本相似度较大的前K个数据的类别最终确定类别，将KNN用于预测问题或者说回归问题上时，过程与之相似，也是考虑到与待预测样本相似度较大的前K个样本的回归值进而来对待预测样本进行预测。

鉴于此，采用KNN对旋转机械进行故障诊断，故障类型为轴承故障，齿轮啮合故障(点蚀)、共振故障、不平衡故障和不对中故障，主代码如下：

%加载故障数据
clc;clear
load bearing.mat % (Ts = 50sec,fs = 1 000)
load gearmesh.mat % (Ts = 50sec, fs = 1 000)
load misalignment.mat % (Ts = 50sec, fs = 1 000)
load imbalance.mat %(Ts = 50sec, fs = 1 000)
load resonance.mat % (Ts = 50sec, fs = 1 000)

Ts = 50; 
Fs = 1000; 
T = 1 / Fs; 
N = 50000; %数据点数
t = (0:N-1); %时间
%%
%----------------------绘制时域图----------------------------------%
featurename = {'bearing','gearmesh','misalignment','imbalance','resonance'};
feature = [bearing,gearmesh,misalignment,imbalance,resonance]; 
% 在时域内绘制每种故障的图形
    for i=1:5
        subplot(5,1,i);
        plot(t,feature(:,i));
        xlabel('time'),ylabel(featurename{i});
        title(['Figure of ',featurename{i},' in time domain']);
    end
%每中故障的单独时域图
figure (1)
plot (t,bearing)  
title ('Time-Domain of bearing-defect rig')
movegui(figure(1),'southeast')
xlabel('Time sec') 
ylabel ('Sampled Measurement')
figure (2)
plot (t,gearmesh) 
title ('Time-Domain of gearmesh rig')
movegui(figure(2),'northeast')
xlabel('Time sec') 
ylabel ('Sampled Measurement')
figure (3)
plot (t,misalignment) 
title ('Time-Domain of misalignment rig')
movegui(figure(3),'northwest')
xlabel('Time sec') 
ylabel ('Sampled Measurement')
figure (4)
plot (t,imbalance) 
title ('Time-Domain of imbalance rig')
movegui(figure(4),'southwest')
xlabel('Time sec') 
ylabel ('Sampled Measurement')
figure (5)
plot (t,resonance) 
title ('Time-Domain of resonance rig')
xlabel('Time sec') 
ylabel ('Sampled Measurement')
movegui(figure(5),'north')

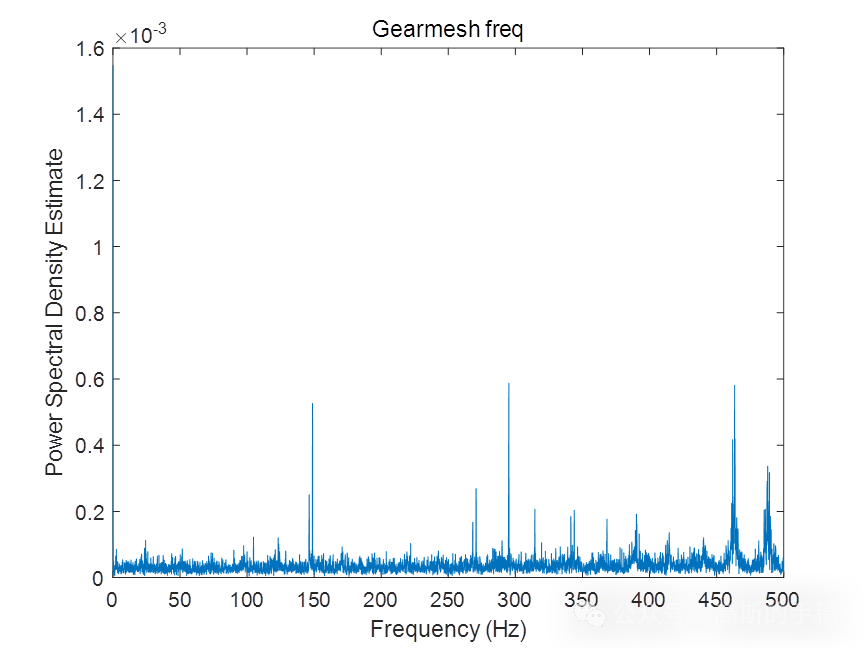
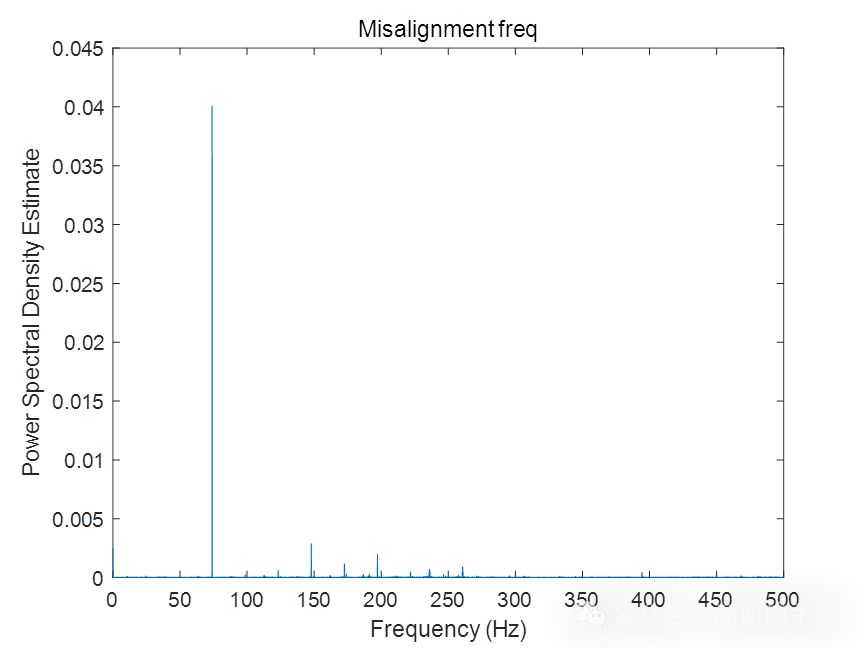
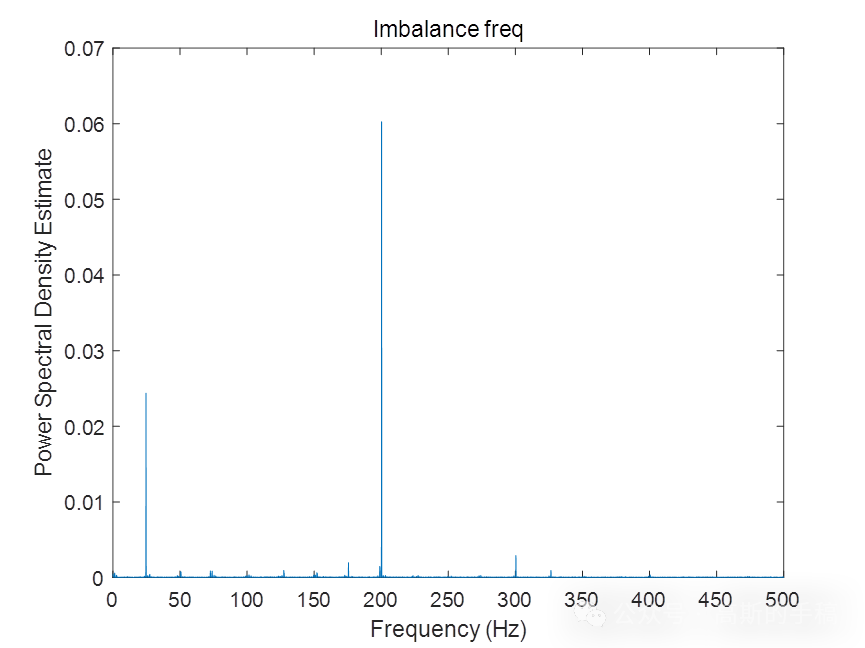
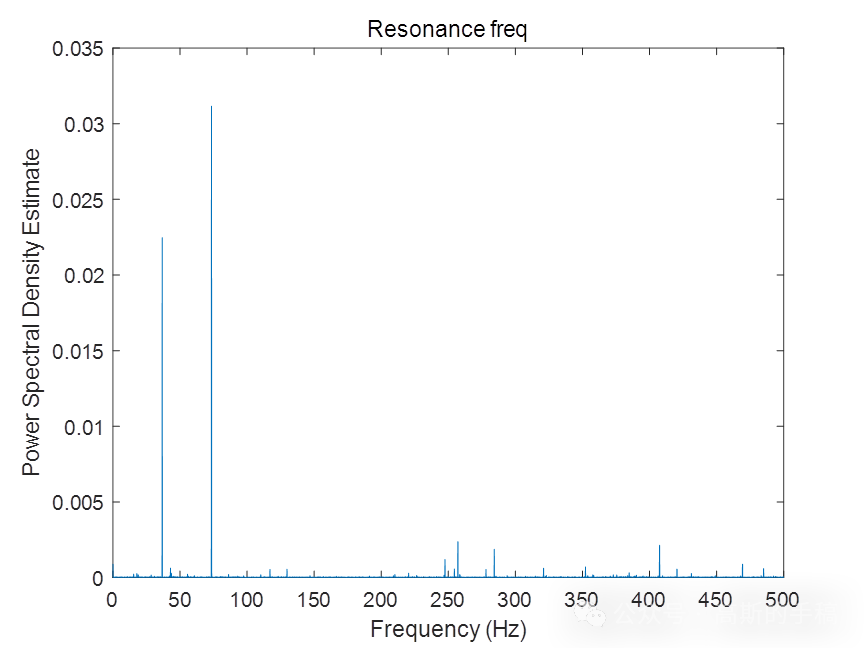
%-----------------频域分析------------------%
[P1,~] = pwelch(bearing,[],[],[],1000); %采样频率1kHz
[P2,~] = pwelch(gearmesh,[],[],[],1000);
[P3,~] = pwelch(misalignment,[],[],[],1000);
[P4,~] = pwelch(imbalance,[],[],[],1000);
[P5,f] = pwelch(resonance,[],[],[],1000);
P = [P1,P2,P3,P4,P5]; %5种故障信号的功率谱密度
til = ["Bearing freq","Gearmesh freq","Misalignment freq","Imbalance freq","Resonance freq"];
%绘图
i = 7;
k = 1;
while i > 6 && i <12
figure (i)
plot(f,P(:,k))
xlabel ('Frequency (Hz)') 
ylabel ('Power Spectral Density Estimate') 
title ({til(1,k)})
i = i +1;
k = k +1;
end 

%----------------------------特征提取--------------------------%
%--------------------重塑矩阵----------------------------------%
reshape_bearing = reshape(bearing,1000,50);
reshape_gearmesh = reshape(gearmesh,1000,50); 
reshape_imbalance = reshape(imbalance,1000,50);
reshape_misalignment = reshape(misalignment,1000,50);
reshape_resonance = reshape(resonance,1000,50); 
%--------------------------预分配速度-----------------------%
x_normalb = zeros(1000,50); x_normalg = zeros(1000,50); 
x_normali = zeros(1000,50); x_normalm = zeros(1000,50);
x_normalr = zeros(1000,50);
 
%----------------------------标准化操作--------------------------------%
for j = 1:50 
    xmean_b = repmat(mean(reshape_bearing(:,j)),1000,1);
    xmean_g = repmat(mean(reshape_gearmesh(:,j)),1000,1);
    xmean_i = repmat(mean(reshape_imbalance(:,j)),1000,1);
    xmean_m = repmat(mean(reshape_misalignment(:,j)),1000,1);
    xmean_r = repmat(mean(reshape_resonance(:,j)),1000,1);
    
    x_normalb(:,j) = reshape_bearing(:,j) - xmean_b; %Bearing 
    x_normalg(:,j) = reshape_gearmesh(:,j) - xmean_g; %GearMesh     
    x_normali(:,j) = reshape_imbalance(:,j) - xmean_i; % Imbalance 
    x_normalm(:,j) = reshape_misalignment(:,j) - xmean_m;% Misalignment 
    x_normalr(:,j) = reshape_resonance(:,j) - xmean_r; % Resonance 
    
end 
% 保存标准化后的数据
save normalized_bearing x_normalb
save normalized_gearmesh x_normalg
save normalized_imbalance x_normali
save normalized_misalignment x_normalm
save normalized_resonance x_normalr
%------------------------第一个特征：f1--------------------------------------%
for k = 1:50 
    [PSD_b(:,k),f1] = pwelch(x_normalb(:,k),[],[],[],1000); 
    [PSD_g(:,k),f1] = pwelch(x_normalg(:,k),[],[],[],1000);
    [PSD_i(:,k),f1] = pwelch(x_normali(:,k),[],[],[],1000);
    [PSD_m(:,k),f1] = pwelch(x_normalm(:,k),[],[],[],1000); 
    [PSD_r(:,k),f1] = pwelch(x_normalr(:,k),[],[],[],1000);
end 
for k1 = 1:50
    f1_b(:,k1) = (norm(PSD_b(:,k1))) / sqrt(max(size(PSD_b)));
    f1_g(:,k1) = (norm(PSD_g(:,k1))) / sqrt(max(size(PSD_g)));
    f1_i(:,k1) = (norm(PSD_i(:,k1))) / sqrt(max(size(PSD_i)));
    f1_m(:,k1) = (norm(PSD_m(:,k1))) / sqrt(max(size(PSD_m)));
    f1_r(:,k1) = (norm(PSD_r(:,k1))) / sqrt(max(size(PSD_r)));
end
%------------------第二个特征(Butterworth) Feature f2-------------------------------%
[B,A] = butter(11,0.1);  %第11阶低通巴特沃斯数字滤波器
f2_b = filter_extract(B,A,x_normalb,Fs);
f2_g = filter_extract(B,A,x_normalg,Fs); 
f2_i = filter_extract(B,A,x_normali,Fs); 
f2_m = filter_extract(B,A,x_normalm,Fs); 
f2_r = filter_extract(B,A,x_normalr,Fs); 

%--------------------------第三个特征Band pass Filter f3 (50 - 200 Hz)-------------%
[B,A] = butter(13,[0.1 0.4]); %13th Order 

f3_b = filter_extract(B,A,x_normalb,Fs);
f3_g = filter_extract(B,A,x_normalg,Fs); 
f3_i = filter_extract(B,A,x_normali,Fs); 
f3_m = filter_extract(B,A,x_normalm,Fs); 
f3_r = filter_extract(B,A,x_normalr,Fs); 

%---------------------------第四个特征High pass Filter f4 (200Hz)-------------------%
[B,A] = butter(18,0.4,'high');

f4_b = filter_extract(B,A,x_normalb,Fs);
f4_g = filter_extract(B,A,x_normalg,Fs); 
f4_i = filter_extract(B,A,x_normali,Fs); 
f4_m = filter_extract(B,A,x_normalm,Fs); 
f4_r = filter_extract(B,A,x_normalr,Fs); 


%------------------------数据可视化--------------------%
%由于有四个特征，利用主成分分析（PCA）进行降维
f1_b1 = transpose(f1_b); f2_b1 = transpose(f2_b);
f3_b1 = transpose(f3_b); f4_b1 = transpose(f4_b); 
f1_g1 = transpose(f1_g); f2_g1 = transpose(f2_g);
f3_g1 = transpose(f3_g); f4_g1 = transpose(f4_g);
f1_i1 = transpose(f1_i); f2_i1 = transpose(f2_i);
f3_i1 = transpose(f3_i); f4_i1 = transpose(f4_i);
f1_m1 = transpose(f1_m); f2_m1 = transpose(f2_m);
f3_m1 = transpose(f3_m); f4_m1 = transpose(f4_m);
f1_r1 = transpose(f1_r); f2_r1 = transpose(f2_r);
f3_r1 = transpose(f3_r); f4_r1 = transpose(f4_r); 

%特征矩阵
f_b = [f1_b1,f2_b1,f3_b1,f4_b1]; %Bearing fault features 
f_g = [f1_g1,f2_g1,f3_g1,f4_g1]; %Gearmesh fault features 
f_i = [f1_i1,f2_i1,f3_i1,f4_i1]; %Imbalance fault features 
f_m = [f1_m1,f2_m1,f3_m1,f4_m1]; %Misalignment fault features 
f_r = [f1_r1,f2_r1,f3_r1,f4_r1]; %Resonance fault features 
%保存
save bearing_features.mat f_b
save gearmesh_features.mat f_g
save imbalance_features.mat f_i
save misalignment_features.mat f_m
save resonance_features.mat f_r 

load bearing_features.mat 
load gearmesh_features.mat 
load imbalance_features.mat
load misalignment_features.mat 
load resonance_features.mat 

G = [f_b ; f_g ; f_i ; f_m ; f_r]; %故障特征结合

c = corrcoef(G); %G的相关系数矩阵 
[v,d] = eig(c); %特征分解
T = [v(:,end)' ; v(:,end-1)']; 

z = T*G'; %创建一个2维特征向量z
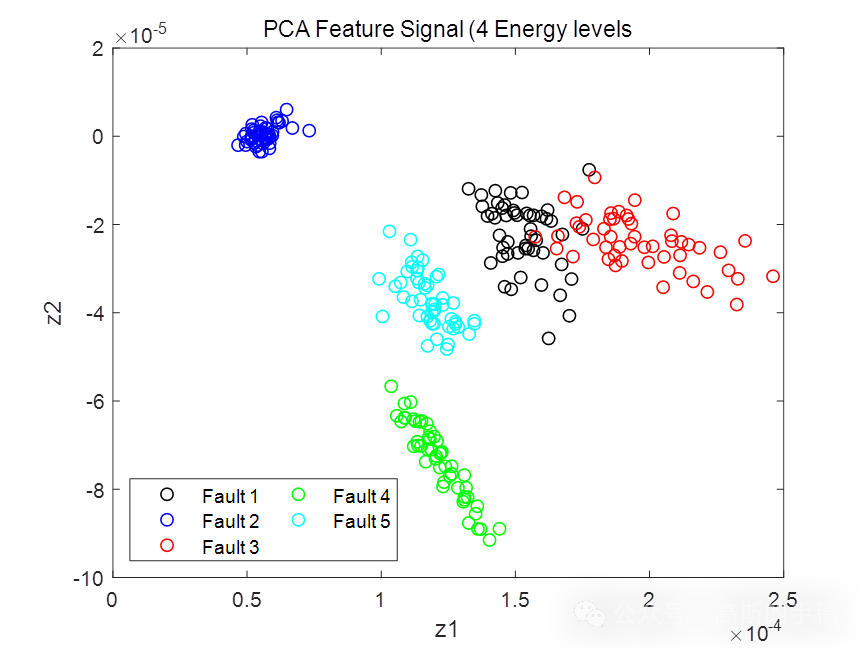
%二维特征的散点图
figure (13)
plot(z(1,1:50), z(2,1:50),'ko') ; hold on 
plot(z(1,51:100), z(2,51:100),'bo'); hold on 
plot(z(1,101:150), z(2,101:150),'ro'); hold on 
plot(z(1,151:200), z(2,151:200),'go'); hold on 
plot(z(1,201:250), z(2,201:250),'co'); hold off
xlabel ('z1'); ylabel('z2'); 
legend({'Fault 1','Fault 2','Fault 3','Fault 4','Fault 5'},'Location',...
    'southwest','NumColumns',2)
title('PCA Feature Signal (4 Energy levels')

Fault_1 = z(:,1:50)';
Fault_2 = z(:,51:100)';
Fault_3 = z(:,101:150)';
Fault_4 = z(:,151:200)';
Fault_5 = z(:,201:250)';

%保存
save Fault_1 Fault_1  
save Fault_2 Fault_2 
save Fault_3 Fault_3 
save Fault_4 Fault_4 
save Fault_5 Fault_5
%%
%------------------------------基于最近邻算法的模式分类--------------------%
%最近邻算法
%加载故障特征 
load Fault_1 %Bearing Fault  
load Fault_2 % Gearmesh Fault 
load Fault_3 % Imbalance Fault 
load Fault_4 % Misalignment Fault 
load Fault_5 % Resonance Fault 


%训练数据-用于构建分类器
%测试数据-用于评估分类器的性能
NoOfTrainingCases = 35;  
NoOfTestingCases = length(Fault_1) - NoOfTrainingCases; 
% 训练数据(前 35 个数据)
trainingSet = [Fault_1(1:NoOfTrainingCases,:);
    Fault_2(1:NoOfTrainingCases,:); 
    Fault_3(1:NoOfTrainingCases,:);
    Fault_4(1:NoOfTrainingCases,:); 
    Fault_5(1:NoOfTrainingCases,:)]; 
% 测试数据
testingSet = [Fault_1(NoOfTrainingCases+1:end,:);
    Fault_2(NoOfTrainingCases+1:end,:);
    Fault_3(NoOfTrainingCases+1:end,:); 
    Fault_4(NoOfTrainingCases+1:end,:); 
    Fault_5(NoOfTrainingCases+1:end,:)];  
%----------最近邻搜索模型的初始化-----------%
% 标签集合
trainingTarget = [ones(1,NoOfTrainingCases),... 
    ones(1,NoOfTrainingCases)*2,...
    ones(1,NoOfTrainingCases)*3,...
    ones(1,NoOfTrainingCases)*4,...
    ones(1,NoOfTrainingCases)*5];

testingTarget = [ones(1,NoOfTestingCases),... 
    ones(1,NoOfTestingCases)*2,...
    ones(1,NoOfTestingCases)*3,...
    ones(1,NoOfTestingCases)*4,...
    ones(1,NoOfTestingCases)*5];
%----------------------------最近邻搜索-----------------%
totalNoOfTestingCases = NoOfTestingCases * 5;
totalNoOfTrainingCases = NoOfTrainingCases * 5;

inferredlabels = zeros(1,totalNoOfTestingCases); 

for unlabelledCaseIdx = 1:totalNoOfTestingCases
    unlabelledCase = testingSet(unlabelledCaseIdx, :); 
    
    
    shortestDistance = inf;
    shortestDistanceLabel = 0; %分配临时标签
    
    
    for labelledCaseIdx = 1:totalNoOfTrainingCases 
        labelledCase = trainingSet(labelledCaseIdx, :); 
        
        %计算 Euclidean距离
        currentDist = euc(unlabelledCase,labelledCase);
        
        %查验距离
        if currentDist < shortestDistance 
            shortestDistance = currentDist; 
            shortestDistanceLabel = trainingTarget(labelledCaseIdx);
        end 
    end 
    
    inferredlabels(unlabelledCaseIdx) = shortestDistanceLabel; 
end 

% 正确分类的样本数量
Nc = length(find(inferredlabels == testingTarget));
%所有样本的数量
Na = length(testingTarget);

%分类的准确率
Acc = 100*(Nc/Na); 
disp(Acc)

原文地址：https://blog.csdn.net/2401_88845856/article/details/143809904

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！