计算机网络前三章计算题总结
计算题
[针对遇到的计算题总结]
PPP帧
异步传输--字节填充
一句话就是[添加转义字符,并特殊改变]
转义字符7D[01111101] 十进制是125 [4个二进制位是1个十六进制位,A是10[十进制],以此类推]
数据部分出现7E >7D5E [添加转义字符,并将7E-20[16进制] 得到5E]
数据部分出现7D >7D5D [同上面]
若数据部分出现不足20[16进制] >7D+(原数据+0x20)
详细计算方法
7E的计算
7E减去 16进制的20。先把7E转化为10进制的126,20转化为十进制32,126-32=94,把94转化为2进制,再每4个二进制位转化为16进制。01011110[5E]
不足0x20的计算
例如0x03
0x03->3, 0x20->32, 3+32=35, 35->00100011[0x23]
即 03 >7D23
为什么针对7E、7D。要做特殊变化?
因为PPP帧的首部第一个字段和尾部最后一个字段都是标志字段,规定为7E。
标志字段表示一个帧的开始和结束。也是帧的定界符。所以在首部的7E和尾部7E之间不应再次出现7E。所以用字节填充方式,替换''假''的7E
同样7D,是我们添加的转义字符,再次出现也要变化。
同步传输--零比特填充
一句话就是[5个连续1加一个0]
太简单,一句话就可以做题了。
例题检验
学完了,做个题检验一下。
发送方发送的PPP帧的数据部分(用十六进制写出)是7E AB 7D 29。试问: (1)若PPP使用异步传输时,线路上实际传输的数据是什么?(用十六进制写出)。 (2)若PPP使用同步传输时,线路上实际传输的数据是什么?(用二进制写出)。
解(1)
7D 5E AB 7D 5D 29
(2)
[数据可以用这样16进制表示,也可以用二进制表示,都是等价的,十六进制为了人好看,二进制是机器原本的]
原数据先转化为二进制是:
01111110 10101011 01111101 00101001 [你会转换吗?] [其实很简单,把每一个字符转化为4个二进制位就行]
零比特填充就是
0111110101010101101111100100101001 [看不清?我再用一个16进制位,也就是4个二进制位演示一遍]
0111 11010 1010 1011 0111 11001 0010 1001 [这下总会了吧]
CRC检验
先讲原理
CRC中文名循环冗余检验,是一种检验方法。FCS中文名冗余码。
通信双方事先规定一个除数p(n位数),对原数据分组,一个组是k个数字(比特)。
要发送的数据是:原码(k位)+冗余码(n-1位)=k+n-1位。
冗余码比除数p少一位,冗余码得到方法是:在原码后添加n-1(也就是冗余码位数一致)个零(k+n-1)。然后除以除数P,得到一个n-1位的余数R,该余数R就是冗余码[FCS]。添加到原码数据后面,就可以发送了(k+n-1)位。
原码k位,除数n位,冗余码n-1位,原码添加n-1位0除以除数得到n-1位的余数。
上面是发送方的发送数据计算过程。
在接收方,对收到的k+n-1位数字,进行除以同样的除数p,得到n-1位的余数。
余数=0:帧对了
余数!=0:错了
具体实现
原理很简单,但是真正计算有必要好好说一下,因为对二进制的除法,取余还是有点陌生的。因此分步一点一点学习吧。
多项式
一般除数P,用一个多项式表示。发送的数据也常用多项式表示。
形如:p(x)=x^3+x^2+1 也称为生成多项式。[多项式的位数是最高位+1]
也就是:p=1101 他是一个4位的,那么余数、冗余码就是3位的。
模二运算
[不考虑借位和进位]
如:原数据101001、除数1101,计算冗余码。
用101001000除以1101得到余数就是结果:
| 1 | 1 | 0 | 1 | 0 | 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | || | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | ||||||||||||
| 1 | 1 | 1 | 0 | ||||||||||||
| 1 | 1 | 0 | 1 | ||||||||||||
| 1 | 1 | 1 | 0 | ||||||||||||
| 1 | 1 | 0 | 1 | ||||||||||||
| 1 | 1 | 0 | 0 | ||||||||||||
| 1 | 1 | 0 | 1 | ||||||||||||
| 0 | 0 | 1 | |||||||||||||
得到余数:001,把添加的3个0,替换就是发送出的数据。
例题检验
若接收方收到的数据T'(X)=X^10+X^8+X^7+X^4+X^3+X,采用CRC校验,生成多项式P(X)=X^4+X^3+1,请完成如下计算: (1)接收方接收到的数据T'(X)对应的比特序列为: (2)生成多项式P(X)对应的比特序列为: (3)模二除法后所得余数为: (4)如果未出现差错,则CRC校验码的比特序列为:
解(1)
10110011010 [这题给出的答案是错的,他给的是10110011001]
(2)
11001
(3)
| 1 | 1 | 0 | 1 | 0 | 1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | || | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 1 | |||||||||||||
| 1 | 1 | 1 | 1 | 0 | |||||||||||||
| 1 | 1 | 0 | 0 | 1 | |||||||||||||
| 1 | 1 | 1 | 1 | 1 | |||||||||||||
| 1 | 1 | 0 | 0 | 1 | |||||||||||||
| 1 | 1 | 0 | 0 | 1 | |||||||||||||
| 1 | 1 | 0 | 0 | 1 | |||||||||||||
| 0 | |||||||||||||||||
余数:0
(4)
本题可以不用计算,因为由(3)得知,余数0,该帧没有差错。那么冗余码就是后面4位,即1010
当然也可以计算得到:
被除数:10110010000。除数:11001。
| 1 | 1 | 0 | 1 | 0 | 1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | || | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 1 | |||||||||||||
| 1 | 1 | 1 | 1 | 0 | |||||||||||||
| 1 | 1 | 0 | 0 | 1 | |||||||||||||
| 1 | 1 | 1 | 1 | 0 | |||||||||||||
| 1 | 1 | 0 | 0 | 1 | |||||||||||||
| 1 | 1 | 1 | 0 | 0 | |||||||||||||
| 1 | 1 | 0 | 0 | 1 | |||||||||||||
| 1 | 0 | 1 | 0 | ||||||||||||||
余数:1010
没做爽?想再做一次?
若待发送数据F(X)=X^9+X^7+X^3+X^2+1,生成多项式P(X)=X^5+X^4+X^2+1,请按要求完成以下计算: (1)发送数据F(X)对应的比特序列为:。 (2)冗余码的位数为: (3)冗余码为: (4)线路上实际传输的二进制数据为:
不知道你是否注意的,本题是待发送数据,上题是接收方收到的数据。
本题数据是原码,上题数据是原码+冗余码
解(1)
1010001101
(2)
除数位数=5+1=6,冗余码位数=6-1=5
(3)
除数:110101,被除数:101000110100000
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 | || | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | ||||||||||||||||
| 1 | 1 | 1 | 0 | 1 | 1 | ||||||||||||||||
| 1 | 1 | 0 | 1 | 0 | 1 | ||||||||||||||||
| 1 | 1 | 1 | 0 | 1 | 0 | ||||||||||||||||
| 1 | 1 | 0 | 1 | 0 | 1 | ||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 0 | ||||||||||||||||
| 1 | 1 | 0 | 1 | 0 | 1 | ||||||||||||||||
| 1 | 0 | 1 | 1 | 0 | 0 | ||||||||||||||||
| 1 | 1 | 0 | 1 | 0 | 1 | ||||||||||||||||
| 1 | 1 | 0 | 0 | 1 | 0 | ||||||||||||||||
| 1 | 1 | 0 | 1 | 0 | 1 | ||||||||||||||||
| 1 | 1 | 1 | 0 | ||||||||||||||||||
算出来余数是:1110,他是4位,而冗余码准确来说应该是5位的。即01110。
可能有的1110也算对。我们按标准写01110
(4)
即发送的数据:也就是原码+冗余码
101000110101110
[这里我不知道是否要零比特填充,遇到再说吧]
最短帧
在CSMA/CD中文名[载波监听多点接入/碰撞检测]。在这里不详细介绍CSMA/CD
现在只需知道最短帧和CSMA/CD有点关系就行了。
争用期:是信号在最远两个端点之间往返传输的时间。也就是两倍的传播时延
最短帧:也就是在争用期时间内,发送的比特数。
对于以太网争用期是512比特,64字节[针对10Mb/s],一般是这样的。
例题检验
现在就可以做题了
某局域网采用CSMA/CD协议实现介质访问控制,数据传输速率为100Mb/s,主机甲和主机乙之间的距离是20km,信号传播速率是200000km/s。若主机甲和主机乙发送数据时产生冲突,则从开始发送数据的时刻起,到两台主机都检测到冲突为止(假设主机甲和主机乙在发送数据的过程中,其他主机不发送数据),则:(1)最短需要多少毫秒。 (2)最长需要多少毫秒。 (3)能使该网络正常运行的最短帧长为多少比特。
解(1)
传播时延t=20000/2*10^8=0.0001s=0.1ms。
最短也就是单程传播时延。怎么理解呢,就是从甲开始发送第一个比特到乙的同时,乙也开始发送第一个比特到甲。
(2)
最长也就是2t,即争用期=0.2ms
这样理解:就是甲发送的第一个比特到达乙的同时,乙开始发送第一个比特到甲。时间是t+t,即2t
(3)
最短帧长=争用期*发送速率(传输速率)=0.2 * 10^-3s * 100 *10 ^6 b/s=20000bit
这里最好写20000bit,别自作聪明写20kbit,因为在表示数据量和速率时 k、M等的进制是不一样的,有时题目为了计算方便,让两个相等。
时延
[时延不是很难、简单回顾一下]
时延=发送时延(传输时延)+传播时延+处理时延+排队时延。
一般后两个不参与计算,因为算不出来。
发送时延=数据长度/发送速率。对于发送速率有很多叫法,有时给出带宽、比特率、数据率希望你知道。
传播时延=信道长度/电磁波在信道上传播速度。1km光纤链路传播时延是5微妙(us)=0.005ms。
例题检验
收发两端之间的传输距离为1000km,信号在媒体上的传播速率为2×10^8m/s。试计算当数据长度为10^3bit,数据发送速率为1Gb/s时, 传播时延为:多少毫秒。
解:传播时延=10^6/2 * 10^8=0.005s=5ms
考虑一个最大距离为2km的局域网,当带宽等于多少Mbps时,传播时延(传播速率为2*10^8m/s)等于512B分组的发送延时。
解:传播时延=2000/ 2* 10^8=10 ^-5s
发送时延=512B/带宽=512*8bit/带宽=10^-5s
带宽=409600000bit/s=409.6Mbit/s=409.6Mbps
交换机自学习
如果是两个交换机,则两个表都要对应更新
[意会吧,没什么原理]
例题检验
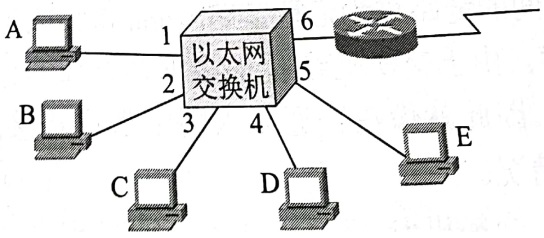
在下图中,以太网交换机有6个接口,分别接了5台主机和一个路由器。在下面表中的“动作”一栏中,表示先后发送了4个帧。假定在开始时,以太网交换机的交换表是空的。试把该表中其他的栏目都填写完。(注意:主机MAC地址请用主机旁的字母表示,
| MAC地址 | 端口 | 写入/更新 | 向那些端口转发 | |
|---|---|---|---|---|
| A->D | A | 1 | 写入 | 除1以外所有端口 |
| D->A | D | 4 | 写入 | 1 |
| E->A | E | 5 | 写入 | 1 |
| A->E | A | 1 | 更新 | 5 |
多种编码方式
原理介绍
[相对性太高,没有绝对的确定]
不归零制:正电平代表1。
曼彻斯特:中间向上跳变是0。也可以反过来。
差分曼彻斯特:开始跟前面一致是1。
例题检验
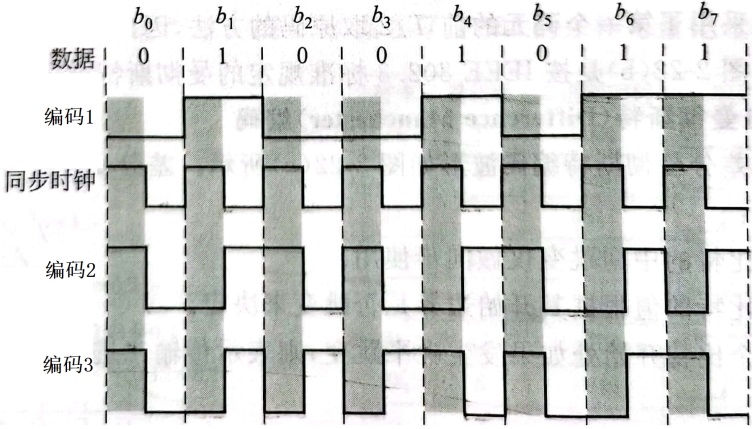
使用三种编码方案对比特流01001011 进行编码的结果如下图所示,则:
-
编码1是不归零制编码。
-
编码2是曼彻斯特编码。[这里反过来定义]
-
编码3是差分曼彻斯特编码。
以下三个编码波形图分别采用了调幅、调频和调相编码方案,则其对应的二进制数据序列分别为: (1)调幅:
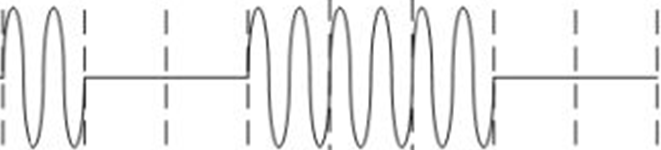
对应的二进制数据为:10011100。 (2)调频:

对应的二进制数据为:10011100。 (3)调相:
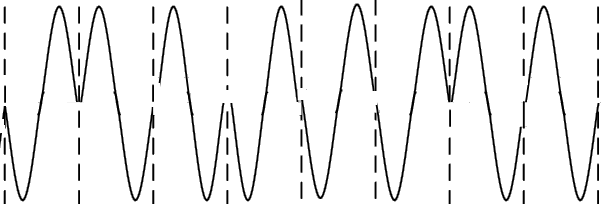
对应的二进制数据为:10011100
以下三个编码波形图分别采用了不归零制、曼彻斯特和差分曼彻斯特编码方案,则其对应的二进制数据序列分别为:
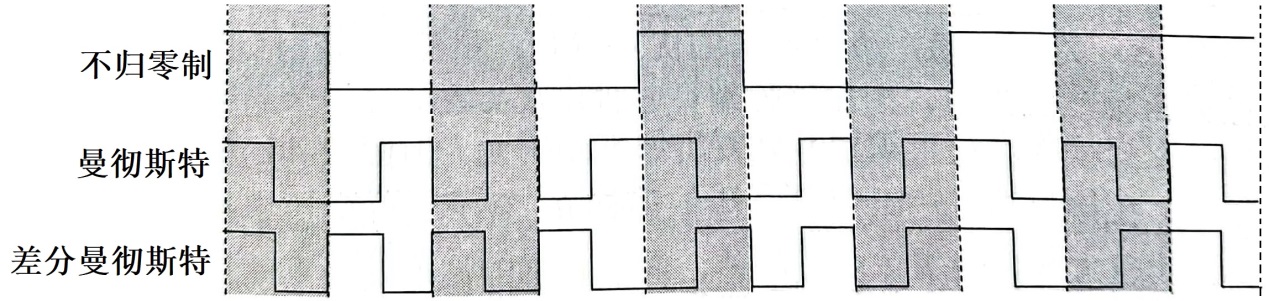
(1)采用不归零制编码方案的波形图对应的二进制数据为:1000100111。 (2)采用曼彻斯特编码方案的波形图对应的二进制数据为:1000100111。 (3)采用差分曼彻斯特编码方案的波形图对应的二进制数据为:1000100111。这个由于不知道第一个和最后一个。答案不确定,根据上面相同编码写的。
波特率与比特率
[见第二章计算题]
CDMA编码
[挺难的,我们应该考不到,遇到题目再学]
原文地址:https://blog.csdn.net/2301_79929720/article/details/143660637
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
