算法导论 总结索引 | 第三部分 第十章：基本数据结构

第三部分：数据结构

1、不同的算法 可能需要 对集合执行不同的操作。例如，许多算法 只需要能在一个集合中 插入和删除元素，以及测试元素 是否属于集合。支持这些操作的动态集合 称为字典
其他一些算法需要更复杂的操作，例如：堆排序中 介绍的 最小优先队列，它支持 向集合中插入一个元素 和 从中取出一个最小元素的操作

2、动态集合的元素：一些类型的动态集合 假定对象中的一个属性 为标识关键字（key）。如果关键字 全不相同，可以 将动态集合 视为一个关键字值的集合。对象可能 包含卫星数据，它们 与其他对象属性 一起移动，除此之外，集合实现不使用它们。对象也可以 有由集合操作使用的属性；这些属性可能 包含有关集合中 其他对象的数据 或 指针

一些动态集合 以其关键字来自于某个全序集 为前提条件，例如，全序关系 允许定义一个集合的最小元素，也可以 确定比集合中一个给定元素大的 下一个元素

3、动态集合上的操作 可以分为两类：简单返回有关集合信息的查询操作 和 改变集合的修改操作

SUCCESSOR(S,x)：一个查询操作，给定关键字属于全序集S的一个元素x，返回S中比x大的前一个元素的指针；如果x为最大元素，则返回NIL
PREDECESSOR(S, x)：一个查询操作，给定关键字属于全序集S的一个元素x，返回S中比x小的前一个元素的指针；如果x为最小元素，则返回NIL

在某些情况下，能够将 SUCCESSOR 和 PREDECESSOR 查询操作 推广应用到一些具有相同关键字的集合上。对于一个有n个关键字的集合，通常的假设是 调用一次MAXIMUM后再调用 n - 1次 SUCCESSOR, 就可以 按序枚举出 该集合中的所有元素

1、栈和队列

1、栈和队列 都是动态集合，且在其上 进行 DELETE 操作所移除的元素是预先设定的

栈实现的是 一种后进先出策略；队列实现的是 一种先进先出策略

2、栈：栈上的INSERT操作称为压入 (PUSH)，而无元素参数的 DELETE 操作 称为弹出 (POP）

可以用一个数组 S[1…n] 来实现 一个最多可容纳n个元素的栈。该数组 有一个属性 S.top，指向 最新插入的元素
当 S.top = 0（数组下标从1 开始）时，栈中不包含任何元素，即 栈是空的。要测试一个栈 是否为空 可以用查询操作 STACK-EMPTY。试图 对一个空栈 执行弹出操作，则 称栈下溢，这通常是个错误。如果 S.top 超过了 n，则称为 栈上溢（下面伪代码 不考虑栈的上溢问题）

STACK-EMPTY(S)
if S.top == 0
return TRUE
else return FALSE

PUSH(S, x)
S.top = S.top + 1
S[S.top] = x

POP(S)
if STACK-EMPTY(S)
error "underflow"
else S.top = S.top - 1
return S[S.top + 1]

3、队列：队列上的 INSERT 操作 称为入队（ENQUEUE），DELETE 操作 称为出队（DEQUEUE）; DEQUEUE 操作也没有元素参数

循环实现：利用数组 Q[1…n] 来实现 一个最多容纳 n - 1 个元素的队列的一种方式。该队列有一个属性 Q.head 指向队头元素，而属性 Q.tail 则指向 下一个新元素将要插入的位置

当 Q.head == Q.tail 时，队列为空。初始有 Q.head == Q.tail == 1
为了 处理上溢 需要舍弃一个元素，Q.head == Q.tail + 1 表示队满，Q.head == Q.tail 表示队空

ENQUEUE(Q, x)
    if Q.head == Q.tail + 1
        error "overflow"
    else Q[Q.tail] = x
        if Q.tail == Q.length
            Q.tail = 1
        else Q.tail = Q.tail + 1
 
DEQUEUE(Q)
    if Q.head == Q.tail
        error "underflow"
    else x = Q[Q.head]
        if Q.head = Q.length
            Q.head = 1
        else Q.head = Q.head + 1
        return x

4、双端队列（deque），其插人和删除操作都可以在两端进行。写出4个时间均为 O(1) 的过程，分别实现在双端队列的两端 插入和删除元素的操作，该队列 是用一个数组实现的

左头右尾，用完了到另一端头尾左右不变

HEAD_ENQUEUE(Q, x)
    if Q.head == Q.tail + 1
        error "overflow"
    else
        if Q.head == 1
            Q.head = Q.length
        else Q.head = Q.head - 1
        Q[Q.head] = x
 
TAIL_ENQUEUE(Q, x)
    if Q.head == Q.tail + 1
        error "overflow"
    else Q[Q.tail] = x
        if Q.tail == Q.length
            Q.tail = 1
        else Q.tail = Q.tail + 1
 
HEAD_DEQUEUE(Q)
    if Q.head == Q.tail
        error "underflow"
    else x = Q[Q.head]
        if Q.head == Q.length
            Q.head = 1 // 满了回到头上去取
        else Q.head = Q.head + 1
        return x
 
TAIL_DEQUEUE(Q)
    if Q.head == Q.tail
        error "underflow"
    else
        if Q.tail == 1
            Q.tail = Q.length
        else Q.tail = Q.tail - 1
        x = Q[Q.tail]
        return x

2、链表

1、其中的各对象 按线性顺序排列。数组的线性顺序 是由数组的下标决定的，然而 与数组不同的是，链表的顺序 是由各个对象里的指针决定的

2、双向链表 L的每个元素 都是一个对象，每个对象 有一个关键字key 和 两个指针：next 和 prev。对象中 还可以包含其他的辅助数据（或称卫星数据）

3、如果一个链表是单链接的，则省略 每个元素中的prev指针。如果链表是已排序的，则链表的线性顺序 与链表元素中关键字的线性顺序一致；据此 最小的元素 就是表头元素，而最大的元素 则是表尾元素

在循环链表中，表头元素的 prev指针 指向表尾元素，而表尾元素的 next指针 则指向表头元素

4、链表的搜索

LIST-SEARCH(L, k)
x = L.head
while x != NIL and x.key != k
x = x.next
return x

5、链表的删除：过程 LIST-DELETE 将一个元素x 从链表L中移除

LIST-DELETE(L, x)
if x.prev != NIL
x.prev.next = x.next
else L.head = x.next
if x.next != NIL
x.next.prev = x.prev

6、哨兵是 一个哑对象，其作用是 简化边界条件的处理

有哨兵的双向循环链表，哨兵 L.nil 位于 表头和表尾之间。属性L.nil.next 指向表头，L.nil.prev 指向表尾
一个空的链表 只由一个哨兵构成，L.nil.next 和 L.nil.prev 同时指向 L.nil
可以通过 L.nil.next访问表头，属性 L.head 就不需要

有哨兵的 LIST-SEARCH

LIST-SEARCH(L, k)
x = L.nil.next
while x != L.nil and x.key != k
x = x.next
return x

有哨兵的 LIST-INSERT

LIST-INSERT(L, x)
x.next = L.nil.next
L.nil.next.prev = x
L.nil.next = x
x.prev = L.nil

哨兵基本不能 降低数据结构相关操作的 渐进时间界，但可以降低常数因子。在循环语句中 使用哨兵的好处 往往在于 可以使代码简洁

我们应当慎用哨兵，假如有许多个很短的链表，它们的哨兵 所占用的额外的存储空间会造成 严重的存储浪费

7、哨兵的 LIST-SEARCH 过程中的每一次循环迭代 都需要两个测试：一是检查 x != L.nil ，另一个是 检查 x.key != k。如何在每次迭代中 省略对 x != L.nil 的检查

哨兵是NIL，哨兵的key改成k，从 NIL下一个开始找

LIST-SEARCH'(L, k)
    x = L.nil.next
    L.nil.key = k
    while x.key ≠ k
        x = x.next
    return x

3、指针和对象的实现

1、在没有显式的指针数据类型的情况下 实现链式数据结构的两种方法，将利用 数组的下标来构造对象和指针
1）对象的多数组表示
对每一个属性 使用一个数组表示，用三个数组 来实现之前所述的链表：三个数组项 key[x]、next[x]和prev[x] 一起表示 链表中的一个对象

2）对象的单数组表示
一个对象 占用一段连续的子数组 A[j…k] ，对象中的每个属性 对应从0到k - j之间的一个偏移量，指向该对象的指针 就是下标j
给定一个指针i，要读取i.prev的值，只需要 在指针的值i上 加上偏移量2，所以要读取的是 A[i + 2]

2、对象的分配与释放：向一个 双向链表 表示的动态集合中 插入一个关键字，就必须分配 一个指向该链表表示中 尚未利用的对象的指针
由垃圾收集器 负责确定 哪些对象是未使用的

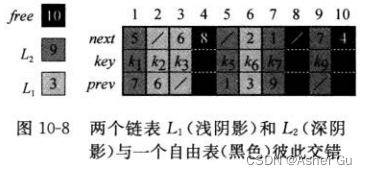
假设 多数组表示法中的 各数组长度为m，且在 某一时刻 该动态集合含有 n<=m 个元素。则n个对象 代表存于 该动态集合中的元素，而 余下的 m - n 个对象是自由的；这些 自由对象可用来 表示将要 插入该动态集合的元素

把 自由对象保存在 一个单链表中，称为 自由表。自由表 只使用 next数组，该数组 只存储 链表中的next指针。该表示中的每一个对象 不是在链表L中，就在自由表中，但不会 同时属于两个表

自由表类似于 一个栈：下一个被分配的对象 就是最后被释放的那个。可以分别利用 栈操作 PUSH和POP的栈表实现形式 来实现 分配和释放对象的过程。假设 下述过程中的 全局变量 free指向自由表的 第一个元素

ALLOCATE-OBJECT()
if free == NIL
error "out of space"
else x = free
free = x.next
return x;

FREE-OBJECT(x)
x.next = free
free = x

链表（浅阴影部分）和自由表（深阴影部分），箭头 标示 自由表的结构

甚至可以 让多个链表共用一个 自由表

可以将其改造，让对象中的 任意一个属性 都可以像 自由表的next属性一样使用，从而使 其可以对 任何同构的对象组 都适用

3、序列<13，4，8，19，5，11>
多数组表示的双向链表

单数组表示的形式（pre+num+next）

4、有根树的表示

1、用链式数据结构 表示有根树 的问题，在 二叉树T中 如何利用属性 p、left和right 存放指向 父节点、左孩子 和 右孩子的指针

2、二叉树的表示方法 可以推广到 每个结点的孩子数至多为常数k的 任意类型的树；只需要将left和night属性 用child1，child2, …, childk 代替。当孩子的结点数 无限制时，这种方法就失效了，因为我们不知道 应当预先分配多少个属性（在多数组表示法中 就是多少个数组）
即使孩子数k 限制在 一个大的常数以内，但若 多数结点只有少量的孩子，则会浪费大量存储

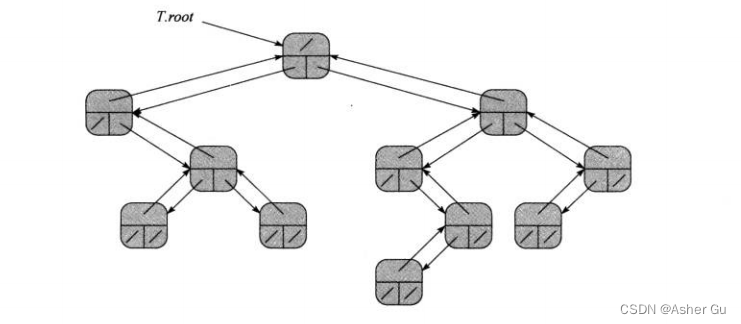
有一个巧妙的方法可以用来表示孩子数任意的树。该方法的优势在于，对任意个结点的有根树，只需要 O(n) 的存储空间，这种左孩子右兄弟表示法，每个节点 都包含一个 父节点指针p，且 T.root 指向树T的根结点。每个节点中 不是包含 指向每个孩子的指针，而是只有两个指针
1）x.left-child 指向 结点x最左边的孩子结点
2）x.right-child 指向 x右侧相邻的 兄弟结点

结点x没有 孩子结点，则 x.left-child = NIL；如果 结点x是 其父结点的 最右孩子，则 x.right-sibling = NIL

3、树的其他表示方法：对一棵完全二叉树 使用 堆来表示，堆 用一个单数组 加上 堆的最末结点下标表示

4、左孩子右兄弟树的递归与非递归、深度与广度遍历
来自 https://blog.csdn.net/fycy2010/article/details/47406813

左孩子右兄弟存储方式：

struct tree_node
{
  int data;
  tree_node* first_child;
  tree_node* sibling;
}

1）深度遍历:
(1) 递归算法:
先根遍历

void preOrder(tree_node *root)
{
if (!root)
return;
printf(root->data);
tree_node* p;
for (p = root->first_child; p; p = p->sibling)
{
    preOrder(p);
    }
}

后根遍历

void postOrder(tree_node *root)
{
if (!root)
return;
tree_node* p;
for (p = root->first_child; p; p = p->sibling)
{
    postOrder(p);
    }
    printf(root->data);
}

(2)非递归算法：
记忆技巧是 将节点看成是二叉树，因为树对应的二叉树的先序 与 树的先根遍历序列 是一致的

先根遍历

void preOrder(tree_node* root)
{
stack sk;
    while(root || !sk.empty())
    {
    while(root)
        {
    printf(root->data);
            sk.push(root);
            root = root->first_child;
        }
        root = sk.top(); sk.pop(); // STL要求这样做的
        root = root->sibling; // root可以为空的
}
}

2）广度遍历(按层次次序遍历树的算法)
用队列实现

void levelOrder(tree_node* root)
{
queue q;
q.push(root);
    while (!q.empty())
    {
    root = q.front(); q.pop();
        printf(root->data);
        root = root->first_child;
        while (!root)
        {
        q.push(root);
            root = root->sibling;
        }
}
}

原文地址：https://blog.csdn.net/AsherGu/article/details/137799625

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！