ROS 手眼标定

在机器人操作系统（ROS）环境下，机械臂的手眼标定（Hand-Eye Calibration）是解决机器人视觉系统中相机坐标系与机械臂末端工具坐标系之间转换关系的关键步骤。这一过程确保了机器人能够准确地依据相机拍摄到的图像信息定位和抓取物体。

手眼标定原理：

手眼标定通常基于几何变换理论，通过一组已知的世界坐标系下的目标点及其对应的相机坐标系下的图像特征点来求解从相机坐标系到机械臂末端坐标系的变换矩阵（以及可能需要的从机械臂基座坐标系到世界坐标系的变换）。这个变换矩阵包括旋转和平移分量，可以表示为一个齐次变换矩阵（4x4）

两种主要的手眼标定方式：

    Eye-to-Hand (眼在手外)：

在这种配置中，相机被固定在一个位置，独立于机械臂，并观察机械臂末端工具上的标记物。通过控制机械臂移动到不同的已知位置并记录下对应位置时相机捕捉到的图像数据，可以推算出相机坐标系相对于机械臂末端坐标系的变换关系。

    Eye-in-Hand (眼在手上)：

相机安装在机械臂的末端执行器上，随着机械臂的运动而一起移动。这种情况下，标定更加复杂，因为相机视点随机械臂运动不断变化。但同样可以通过一系列预定的机械臂姿态和相应的图像数据来确定坐标系之间的映射关系。

在ROS中，有多个功能包可以用于完成机械臂的手眼标定以实现目标物体的精准抓取。

以下是几个常用的功能包：

    easy_handeye：

        提供了一种直观易用的方法来进行手眼标定，支持眼在手上（Eye-in-Hand）和眼在手外（Eye-to-Hand）两种配置。该包通常与MoveIt!等运动规划框架配合使用，帮助计算相机相对于机械臂末端执行器的外参数。

    handeye_calib：

        另一个广泛使用的包，它提供了在线或离线手眼标定算法，允许用户通过采集一系列机器人姿态和对应的相机图像数据来估计手眼关系。

    calib_cam_robot 或 cam_robot_calibration：

        这些包也提供了用于手眼标定的基本工具，可能包含多种标定算法，包括传统的棋盘格法、圆点阵列法以及更复杂的优化方法。

    visp_hand2eye_calibration：

        由ViSP（Visual Servoing Platform）项目提供的一个工具，用于进行手眼系统标定，尤其适合那些基于ViSP库开发视觉伺服应用的场景。

因为一个物体与相机的相对位置关系和这个物体与机械臂之间的关系是不一样的，所以在相机确定了物体的位置之后，还要把此时的位置转换成相对于机械臂的位置，这样机械臂才能进行抓取。

手眼标定法的核心公式只有一个，用一个数学模型来表示为AX=XB的形式,其中A代表手的位置和姿态，X代表未知的变换矩阵，B代表视觉系统的位置和姿态。这里的 X 就是指手（机械臂末端）与眼（摄像头）之间的坐标转换关系。

为了得到相机坐标系与机器人坐标系之间的位姿关系，包括两种：eye in hand （相机安装在机械臂末端）和eye to hand (相机安装在机械臂外侧)。

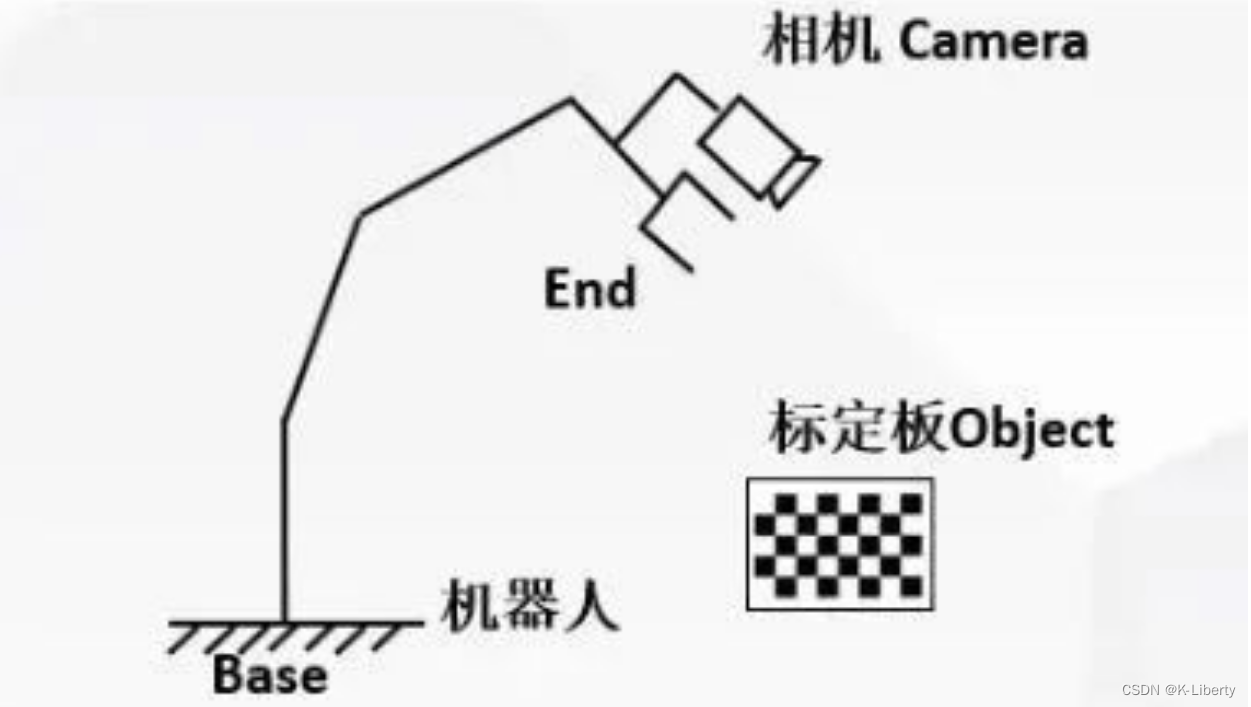
Eye-In-Hand，是指摄像头被安装在机械臂上。此时要求取的是，End到Camera之间的坐标转换关系，也就是这种情况下，有两个变量是不变的：

摄像头与机械臂末端之间的坐标转换关系不变，

标定板与机械臂底座之间的坐标转换关系不变，

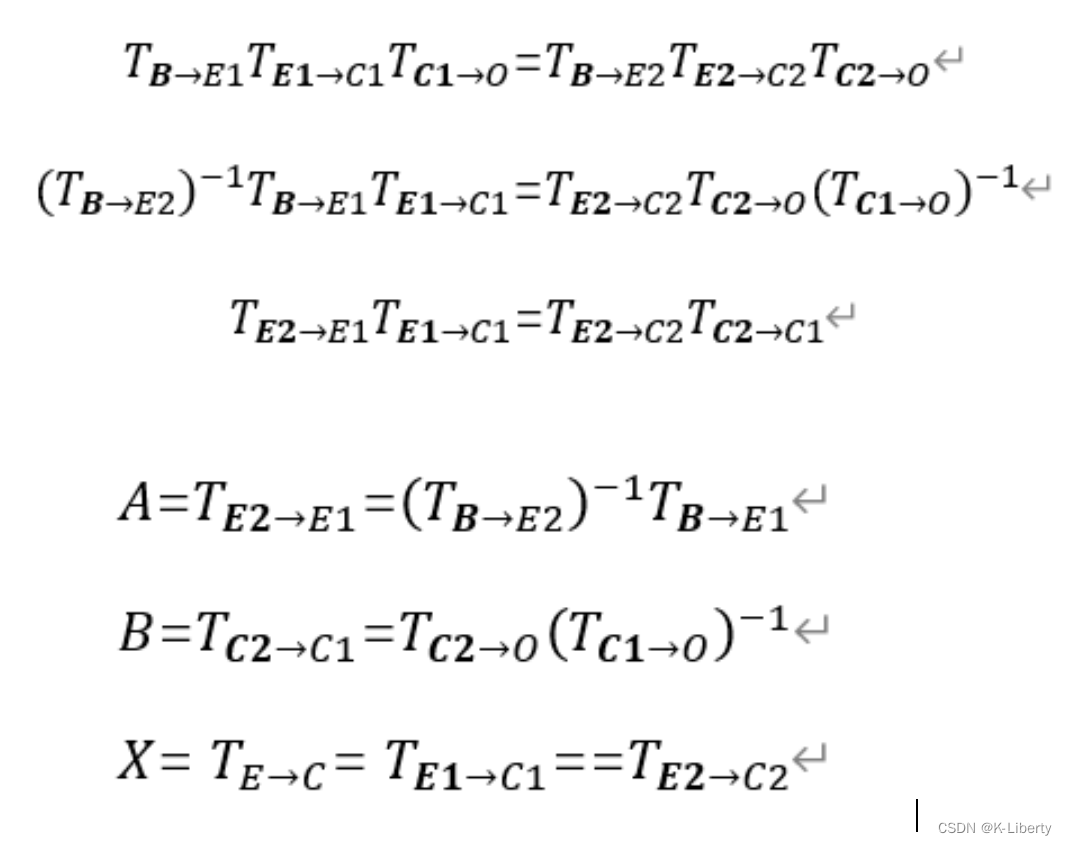
Eye-To-Hand，是指摄像头被安装在一个固定不动的位置，而标定板被拿在机械臂手上。此时要求取的是，Base到Camera之间的坐标转换关系，也就是这种情况下，有两个变量是不变的：

摄像头与机械臂底座之间的坐标转换关系不变，

标定板与机械臂末端之间的坐标转换关系不变，

Eye-In-Hand：相机安装在机械手上，随着机械手一起移动，较为常用。

手眼标定步骤：

1.数据采集：首先收集一系列数据，包括机器人手的位置和姿态以及视觉系统的位置和姿态。这些数据通常通过运动控制和视觉传感器来获取。

2.标定物体选择：为了确保标定的准确性，通常需要选择适当的标定物体，如棋盘格、对称圆或非对称圆等。这些标定物体在图像中容易识别，并且具有已知的尺寸和几何特征。

3.通过机械臂上面的相机，对待测物体进行位姿检测，并且输出参数。

4.输出机械臂末端的位置参数。

5.重复4、5步骤，采集十组以上有效参数。

6.将采集的有效参数放入代码中进行计算。

7.输出手眼转换矩阵。

补充：常见的手眼矩阵表现形式:

欧拉角版

  [x,y,z,rx,ry,rz]

四元数版

   [x,y,z,qx,qy,qz,qw]

旋转矩阵版本

[

 [r11,r12,r13,x],

 [r21,r22,r23,y],

 [r31,r32,r33,z]

]

齐次矩阵

在旋转矩阵版本上增加一行[0,0,0,1]构成齐次矩阵，

[

 [r11,r12,r13,x],

 [r21,r22,r23,y],

 [r31,r32,r33,z]，

 [0, 0, 0, 1]

]

原文地址：https://blog.csdn.net/2301_79503228/article/details/135620888

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！