2024mathorcup(妈妈杯)数学建模C题思路分析-物流网络分拣中心货量预测及人员排班

🕗 发布于 2024-04-14 09:14 数学建模 2024mathorcup 数学建模思路思路分享妈妈杯C题思路

1 赛题

C 题物流网络分拣中心货量预测及人员排班
电商物流网络在订单履约中由多个环节组成，图 ’ 是一个简化的物流网络示意图。其中，分拣中心作为网络的中间环节，需要将包裹按照不同流向进行分拣并发往下一个场地，最终使包裹到达消费者手中。分拣中心管理效率的提升，对整体网络的履约效率和运作成本起着十分重要的作用。
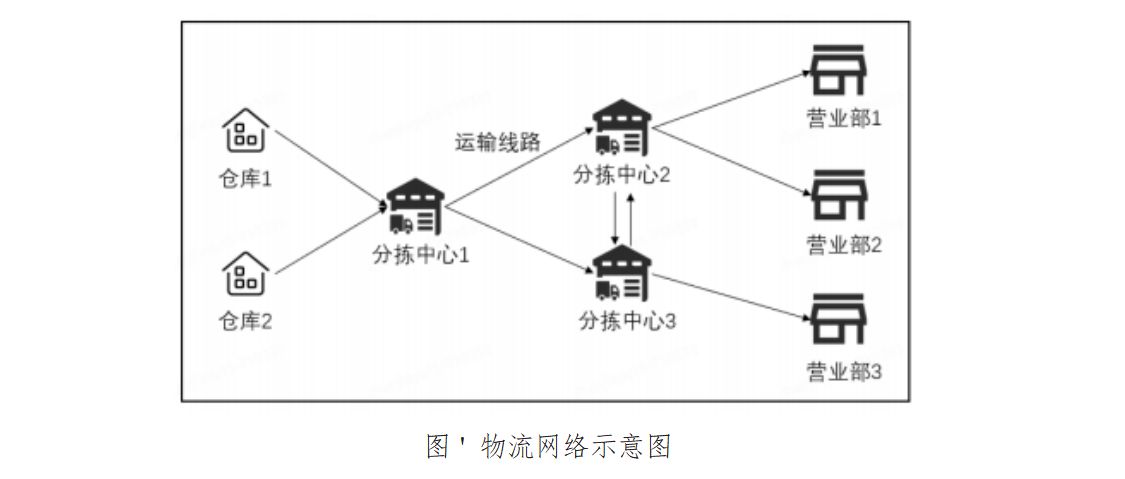
在这里插入图片描述
分拣中心的货量预测是电商物流网络重要的研究问题，对分拣中心货量的精准预测是后续管理及决策的基础，如果管理者可以提前预知之后一段时间各个分拣中心需要操作的货量，便可以提前对资源进行安排。在此场景下的货量预测目标一般有两个：一是根据历史货量、物流网络配置等信息，预测每个分拣中心每天的货量；二是根据历史货量小时数据，预测每个分拣中心每小时的货量。

分拣中心的货量预测与网络的运输线路有关，通过分析各线路的运输货量，可以得出各分拣中心之间的网络连接关系。当线路关系调整时，可以参考线路的调整信息，得到各分拣中心货量更为准确的预测。

基于分拣中心货量预测的人员排班是接下来要解决的重要问题，分拣中心的人员包含正式工和临时工两种：正式工是场地长期雇佣的人员，工作效率较高；临时工是根据货量情况临时招募的人员，每天可以任意增减，但工作效率相对较低、雇佣成本较高。根据货量预测结果合理安排人员，旨在完成工作的情况下尽可能降低人员成本。针对当前物流网络，其人员
安排班次及小时人效指标情况如下：

对于所有分拣中心，每天分为 6 个班次，分别为： 00:00-08:00， 05:00- 13:00 ，08:00- 16:00, 12:00-20:00 ，14:00-22:00 ，16:00-24:00，每个人员（正式工或临时工）每天只能出勤一个班次；
小时人效指标为每人每小时完成分拣的包裹量（包裹量即货量），正式工的最高小时人效为 25 包裹/小时，临时工的最高小时人效为 20包裹/小时。
该物流网络包括 57 个分拣中心，每个分拣中心过去 4 个月的每天货量如附件 1 所示，过去 30 天的每小时货量如附件 2 所示。基于以上数据，请完成以下问题：

问题 1：建立货量预测模型，对 57 个分拣中心未来 30 天每天及每小时的货量进行预测，将预测结果写入结果表 1 和表 2 中。
问题 2：过去 90 天各分拣中心之间的各运输线路平均货量如附件 3 所示。若未来 30 天分拣中心之间的运输线路发生了变化，具体如附件 4 所示。根据附件 1-4，请对 57 个分拣中心未来 30 天每天及每小时的货量进行预测，并将预测结果写入结果表 3 和表 4 中。
问题 3：假设每个分拣中心有 60 名正式工，在人员安排时将优先使用正式工，若需额外人员将使用临时工。请基于问题 2 的预测结果建立模型，给出未来 30 天每个分拣中心每个班次的出勤人数，并写入结果表 5 中。要求在每天的货量处理完成的基础上，安排的人天数（例如 30 天每天出勤 200 名员工，则总人天数为 6000）尽可能少，且每天的实际小时人效尽量
均衡。
问题 4：研究特定分拣中心的排班问题，这里不妨以 SC60 为例，假设分拣中心 SC60 当前有 200 名正式工，请基于问题 2 的预测结果建立模型，确定未来 30 天每名正式工及临时工的班次出勤计划，即给出未来 30 天每天六个班次中，每名正式工将在哪些班次出勤，每个班次需要雇佣多少临时工，并写入结果表 6 中。每名正式工的出勤率（出勤的天数除以总天数 30）不能高于 85% ，且连续出勤天数不能超过 7 天。要求在每天货量处理完成的基础上，安排的人天数尽可能少，每天的实际小时人效尽量均衡，且正式工出勤率尽量均衡。
注：上面四个问题中，除了正常完成论文外，每个问题的输出结果表
请一起压缩为“结果.zip ”压缩包格式，并单独上传至竞赛平台。

2 选题分析

A题属于目标优化问题，还结合了动态规划问题，别看题目描述的复杂，只要构建好目标函数就能轻松解决

B题这种类型的题目这几年出的还不少呀，就是机器学习或深度学习的图像目标检测

C题是一个典型的运筹学问题，涉及到预测模型的建立和优化排班策略的制定。解决这个问题需要综合运用统计学、机器学习、优化算法等多学科知识。

D题该问题是一个典型的优化问题，需要综合考虑多个因素，如设备性能、矿山条件、成本和风险等

本次建模题目难度（由高到低） B>A>D>C

！！！A君会先出C题思路！！！

3 解题思路

3.1 简要分析

具体问题描述如下：

货量预测：需要根据历史数据预测未来不同时间段的货量。文档中提供了一系列的时间段，每个时间段对应一个货量值。这些时间段从00:00-08:00开始，以4小时为一个单位，直到24:00结束。预测的目的是为了更好地安排人员和资源，以应对不同时间段的货量变化。

人员排班：基于货量预测结果，需要制定合理的人员排班计划。文档中提到了不同的排班时间段，例如05:00-13:00，12:00-20:00等，以及每个时间段所需的人员数量。排班计划需要考虑到货量高峰和低谷，以及人员的工作时长和休息时间等因素。

数据分析：首先需要对提供的历史货量数据进行分析，找出货量变化的规律和趋势。这可能涉及到时间序列分析、相关性分析等统计方法。

预测模型构建：根据分析结果，构建一个能够预测未来货量的数学模型。这个模型可能需要考虑到季节性因素、特殊事件、节假日等对货量的影响。

优化排班：在预测模型的基础上，制定人员排班计划。这可以通过运筹学中的排班优化模型来实现，如线性规划、整数规划等，以最小化成本或最大化效率。

验证与调整：最后，需要对预测模型和排班计划进行验证，确保它们在实际操作中的有效性和可行性。根据实际情况的反馈，对模型和计划进行必要的调整和优化。

这个问题是一个典型的运筹学问题，需要综合运用数学建模、统计分析和优化技术来解决。解决这个问题不仅可以提高物流中心的运营效率，降低成本，还可以提升员工的工作满意度和服务质量。

3.2 思路更新

第一问思路已出，第一问本质上就是一个Arima预测即可，详细思路放在文档中

在这里插入图片描述

第二问思路更新

C题第二问思路更新，大家注意第二问一定要构建完整的拓扑网络，网上有资料说是构建最短路即可，完全是错的，快递物流系统往往并不能理想的走最短路，要考虑的是负载均衡(保持原负载不变)

在这里插入图片描述
三四问更新‘
此问题不仅需要预测货量，还需要根据预测结果进行人员排班的优化。这涉及到运筹学中的排班问题，可能需要使用线性规划、整数规划或者其他优化算法来最小化人员成本，同时满足货量处理的需求。

A君给大家构建一个混合整数线性规划（Mixed Integer Linear Programming, MILP）模型作为示范。大家可以根据相同思路构建或优化自己的模型。

该模型的目标是在满足每天货量处理需求的前提下，最小化总人天数，同时尽量保持每天的实际小时人效均衡。

在这里插入图片描述

第四问其实就是在第三问基础上构建约束条件更多的混合整数线性规划模型。

在这里插入图片描述
完整思路放在文档中。

🥇 最新思路更新(看最新发布的文章即可):
https://blog.csdn.net/dc_sinor?type=blog

4 最新思路更新