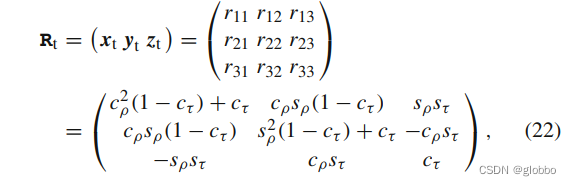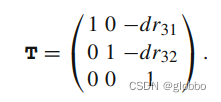射影变换的一种解法
1、欧式变换
参考《计算机视觉中的多视图几何》1.4节定义。
欧式变换也叫等距变换,是刚体运动模型,可以表示为: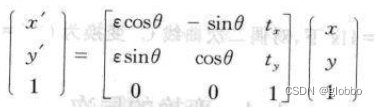
其中的ε=±1,更简洁的形式是:
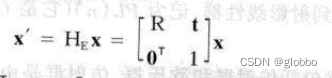
2、相似变换
相似变换是一个等距变换和一个均匀缩放的复合,表示为:
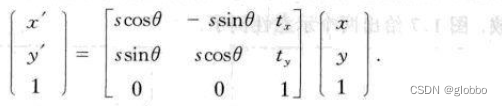
也可以写为:
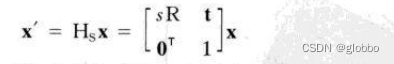
其中的s表示均匀缩放。
不变量 直线的夹角、线段长度的比例、面积的比例。
3、仿射变换
仿射变换是一个非奇异线性变换与一个平移变换的复合,它的矩阵表示:
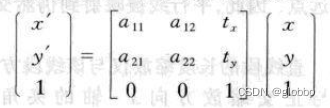
平面仿射变换有6个自由度,可以由3组点来解决。
不变量 平行的线依旧平行,平行线段的长度比不变,面积比不变。
4、射影变换(单应homography)
射影映射是把平面的点映射到另一个平面的点,它也把直线映射到直线。射影映射又称为射影变换或单应变换。——《计算机视觉中的多视图几何》P8
2D平面射影变换是关于齐次3维矢量的一种线性变换,可用一个非奇异的3*3矩阵H表示为:
[
x
′
y
′
t
]
\begin{bmatrix} x^{'} \\ y^{'} \\ t \end{bmatrix}
x′y′t
=
[
h
11
h
12
h
13
h
21
h
22
h
23
h
31
h
32
h
33
]
\begin{bmatrix} h11 & h12 & h13\\ h21 & h22 & h23\\ h31 & h32 & h33 \end{bmatrix}
h11h21h31h12h22h32h13h23h33
[
x
y
1
]
\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
xy1
或者可以写为 x ′ = H x x^{'}=Hx x′=Hx
最终结果:
x ′ = h 11 x + h 12 y + h 13 h 31 x + h 32 y + h 33 x^{'}=\frac{h11x+h12y+h13}{h31x+h32y+h33} x′=h31x+h32y+h33h11x+h12y+h13
y ′ = h 21 x + h 22 y + h 23 h 31 x + h 32 y + h 33 y^{'}=\frac{h21x+h22y+h23}{h31x+h32y+h33} y′=h31x+h32y+h33h21x+h22y+h23
在H的9个元素中,有8个自由度,如何理解由9个变8个呢?给H的元素乘上同一个数a,得到的aH和H作用相同,因为新的H无非把齐次点x变成了齐次点ax,在最终计算时会约掉。因此我们可以把a换成1/h22,那么H就变成了只有8个自由元素的矩阵。
上面的H可以通过构建4组点(三个点不共线)求解这8个未知量,因为每个点对应了两个方程,4个点就对应8个方程。
不变量,四共线点的交比是不变的。
那么射影映射和透视映射的关系是什么呢?结论是透视映射是射影映射的一种。
5、总结
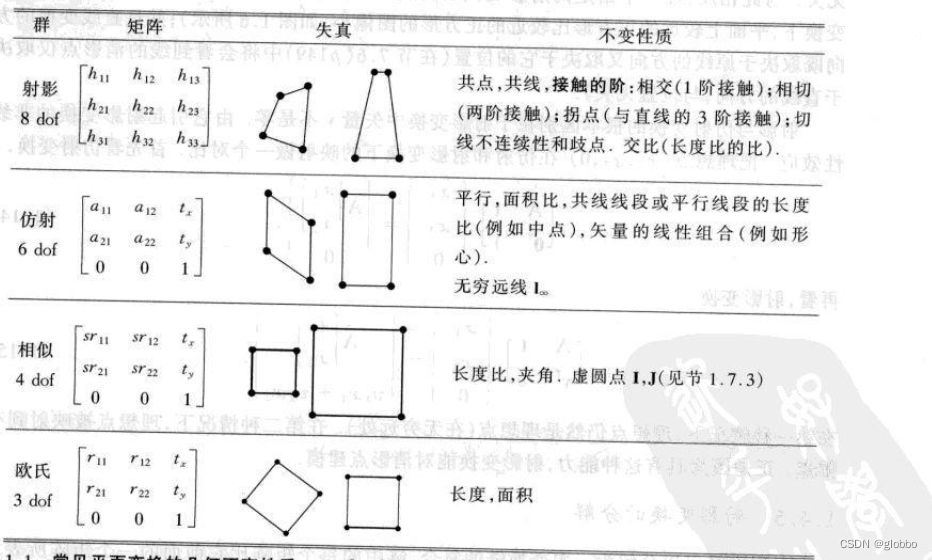
6、透视投影
按照《计算机视觉中的多视图几何》P430的解释,透视变换是射影映射的一种特殊情况,它最终要的一个性质是:
连接对应点的直线,共点。
直线的透视变换:
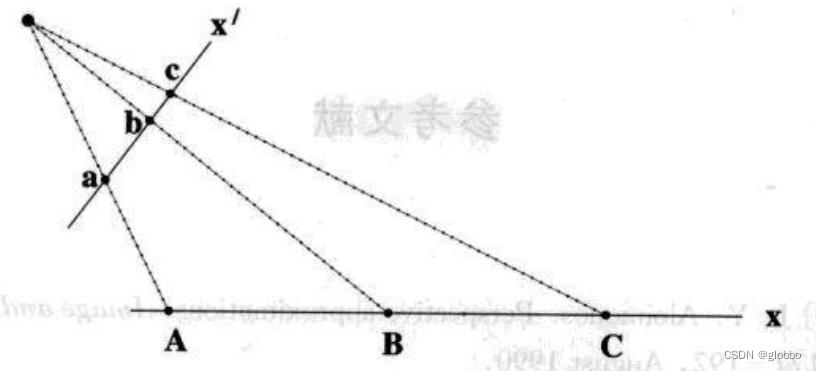
平面的透视变换:
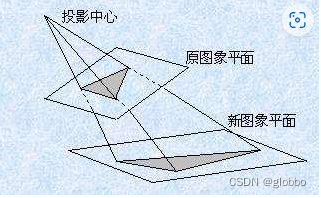
两个透视变换的合成,不是透视变换,因为pqr三个点不共点,但是射影变换:
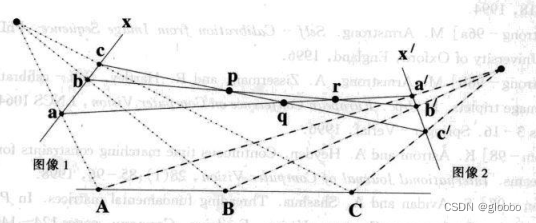
7、摄像机旋转
参考多视图几何7.4.2章节
摄像机在不改变内参时进行旋转,假定世界点X在旋转前的图像坐标x,旋转后的图像坐标x^{'},旋转矩阵R:
x = K X x = KX x=KX
x ′ = K R X = K R K − 1 K X = K R K − 1 X x^{'} = KRX = KRK^{-1}KX = KRK^{-1}X x′=KRX=KRK−1KX=KRK−1X
这里K表示相机内参矩阵。
这个性质常用在图像拼接上,构建全景视图。
8、一种透视投影的解法
这里记录的是一种透视投影下平面点的转换算法,参考steger2017的论文。
【问题描述】
如下图所示,坐标系
(
x
u
,
y
u
,
z
u
)
(x_{u},y_{u},z_{u})
(xu,yu,zu)是水平面,
(
x
t
,
y
t
,
z
t
)
(x_{t},y_{t},z_{t})
(xt,yt,zt)是倾斜面,透视点距离水平面距离为d,两个平面倾斜角为
τ
τ
τ,已知
P
u
P_{u}
Pu,求
P
u
P_{u}
Pu经过透视后在
P
t
P_{t}
Pt中的坐标(已知
P
t
P_{t}
Pt求
P
u
P_{u}
Pu也可以)。
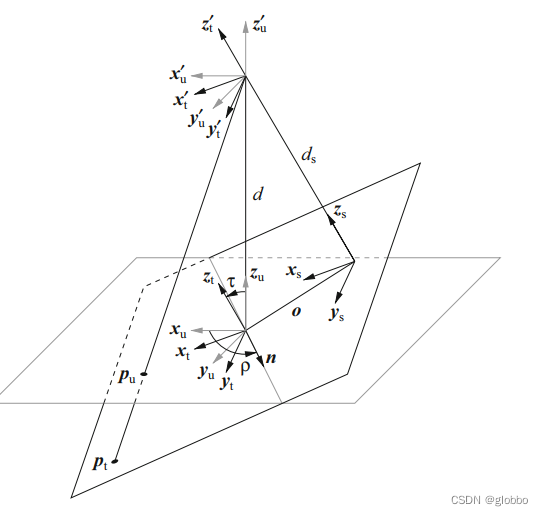
-
(
x
u
,
y
u
,
z
u
)
(x_{u},y_{u},z_{u})
(xu,yu,zu)到
(
x
s
,
y
s
,
z
s
)
(x_{s},y_{s},z_{s})
(xs,ys,zs)
套用上面的摄像机旋转, P s P_{s} Ps = u s T ∗ P u _{u}^{s}\textrm{T}*P_{u} usT∗Pu
u s T _{u}^{s}\textrm{T} usT = K s R K u − 1 K_{s}RK_{u}^{-1} KsRKu−1 -
(
x
s
,
y
s
,
z
s
)
(x_{s},y_{s},z_{s})
(xs,ys,zs)到
(
x
t
,
y
t
,
z
t
)
(x_{t},y_{t},z_{t})
(xt,yt,zt)
是一个平移操作, s t T _{s}^{t}\textrm{T} stT -
(
x
u
,
y
u
,
z
u
)
(x_{u},y_{u},z_{u})
(xu,yu,zu)到
(
x
t
,
y
t
,
z
t
)
(x_{t},y_{t},z_{t})
(xt,yt,zt)
最终的转换矩阵H: H H H = s t T ∗ K s R K u − 1 _{s}^{t}\textrm{T}*K_{s}RK_{u}^{-1} stT∗KsRKu−1
具体参数解释:
K u K_{u} Ku相机内参矩阵,只需要考虑焦距 d d d即可。
K u K_{u} Ku = ( d 0 0 0 d 0 0 0 1 ) \begin{pmatrix} d & 0 & 0\\ 0 & d & 0\\ 0 & 0 & 1 \end{pmatrix} d000d0001
K s K_{s} Ks也是相机内参矩阵,此时焦距变为了 d s d_{s} ds, d s d_{s} ds= c o s τ cosτ cosτ
K s K_{s} Ks = ( d s 0 0 0 d s 0 0 0 1 ) \begin{pmatrix} d_{s} & 0 & 0\\ 0 & d_{s} & 0\\ 0 & 0 & 1 \end{pmatrix} ds000ds0001
R R R旋转矩阵,(参考《机器人建模及控制》2.5.3)即两个平面的旋转矩阵,这里假定平面 ( x u , y u , z u ) (x_{u},y_{u},z_{u}) (xu,yu,zu)绕 n n n轴旋转角度 τ τ τ到 ( x t , y t , z t ) (x_{t},y_{t},z_{t}) (xt,yt,zt), n n n轴和x轴夹角为 ρ ρ ρ,则:
n n n = ( c o s ρ s i n ρ 0 ) \begin{pmatrix} cosρ\\ sinρ\\ 0 \end{pmatrix} cosρsinρ0
s t T _{s}^{t}\textrm{T} stT
最终结果:
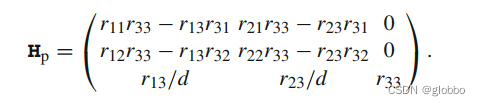
原文地址:https://blog.csdn.net/hao1183716597/article/details/136370641
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!