概率论之正态分布密度函数与matlab

0.浅谈我的想法

众所周知，在这个数学建模的这个过程之中会遇到很多的这个概率论的相关的问题，之前分享过这个假设性检验的这个相关内容，但是那个只是沧海一粟，概率论和数理统计的很多内容都是偏向于理论的，这让原本就是复杂的知识更是雪上加霜，这也让这个概率论成为很多人成长道路上面的这个拦路虎；

因为如果是这个高等数学，线性代数，无非就是进行计算吗，但是这个概率论对于初学者而言，这个印象就是有的时候连这个题目都看不懂，跟别说结合这个具体的方法进行计算了，就算这个题目可以看懂，我认为这个达到的效果就是套用这个公式进行机械的运算，我认为这个违背了初衷，因为我是不喜欢学习这样的理论性课程的，如果只会理论和计算的话；

不知道大学生对于这个概率论是什么样的看法，我也是真的觉得这个概率论和数理统计是应该发挥它的作用的，他应该可以让我们从这个看似不规律的数据里面看到这个趋势或者是共性规律，并且这个概率论在我们的这个数学建模里面进行这个假设性检验和区间估计，显著性水平等等之类的这个知识，都是可以为我们的这个问题提供参考和依据的；

因此，我认为这个概率论不应该沦为这个理论和只会套公式计算的学科，我也不喜欢按照这样的方式进行学习，因此，我决定集合自己喜欢的软件matlab使用数形结合的思想，帮助大家理解这个概率论里面的一些抽象的概念，尤其是各种分布，以数学建模作为依托，希望可以把这个概率论形象起来，因为在我的这个观念里面，概率论的这个理论性太强了，今天，我选择了大家都很熟悉的这个正态分布作为引入：

1.正态分布引入

1.1公式和对应概率

$$\begin{gathered} \mathrm{f}\left(\mathrm{x}\right)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left(\mathrm{x}-\mu \right)}^2}{2{\sigma }^2}\right) \\ \mu \pm \sigma :68\% \\ \mu \pm 2\sigma :95.4\% \\ \mu \pm 3\sigma :99.7\% \end{gathered}$$

1.2模拟生成数据

%randn是 Matlab 中用于生成服从标准正态分布（均值为 0，方差为 1 的正态分布）随机数的函数。它可以按照指定
%的维度要求来生成相应规模的随机数矩阵。
%下面的这个表示的就是生成随机数，这个数据就是一个10000*1的矩阵，也就是10000个数据
data = randn([10000 1]);
%下面的这个函数绘制的是我们的直方图，100表示这个直方图分块的个数，也就是100个小块
h = histogram(data,100)
%下面的这个表示的就是对于这个随机生成的数据进行升序排列
data_up=sort(data,'ascend')

1.3图像绘制

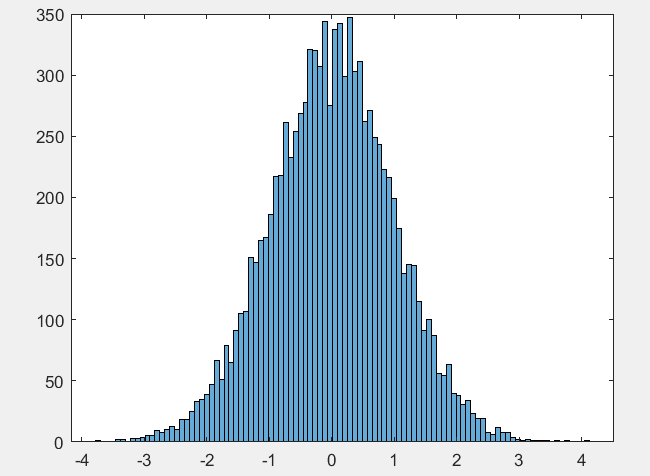
下面的这个就是一个类似于正态分布的情况，但是这个纵坐标表示的就是我们的这个横坐标上面对应的这个数据出现的次数–频数；

当我们的这个随机生成的这个数据的数据数量发生变化的时候，我们的这个纵坐标的这个取值也是会对应发生变化的；

1.4图像的调整

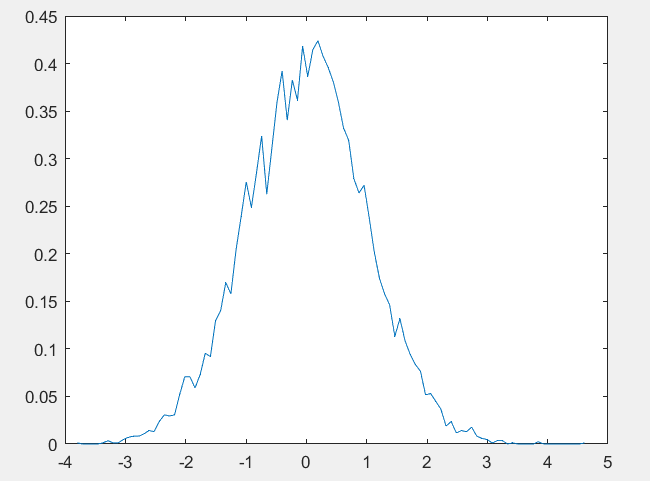
1）下面的这个首先就是把我们的这个图像上面的100个小块的中间点之间连接起来，使用的就是这个小块的左右端点的这个平均值作为参数指标的；

2）最后一行的这个绘图函数的第二个参数表示的就是我们的这个10000里面的这个频数除以这个数据的个数除以这个长条的宽度（我记得在高中学习简单的统计的时候就是这样学习的），就可以转换为我们的这个对应的函数图像，纵坐标表示的就是概率；

3）这个图像围成的（与x轴）就是1，这个就是我们的概率密度函数的雏形；

data = randn([10000 1]);
h = histogram(data,100)
hold on
edges=h.BinEdges
for i=1:100
    edge(i)=(edges(i)+edges(i+1))/2;
end
plot(edge,h.Values)
hold off
%edge表示的就是：查找二维灰度图像中的边缘
plot(edge,h.Values/10000/h.BinWidth)

1.5概率密度函数

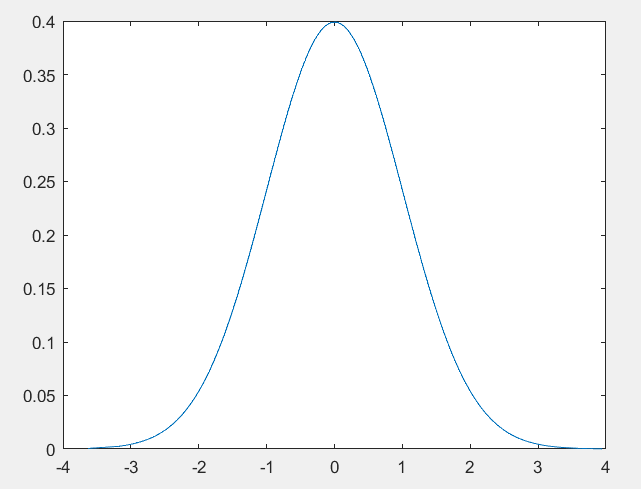
%下面使用的这个函数就是生成我们的这个正态分布的概率密度函数的
%上面的这个随机生成的数据绘制的图像具有一定的随机性，但是下面的这个概率密度函数的这个
%图像就显得很平滑了
y_prob=normpdf(data_up,0,1);
plot(data_up,y_prob)

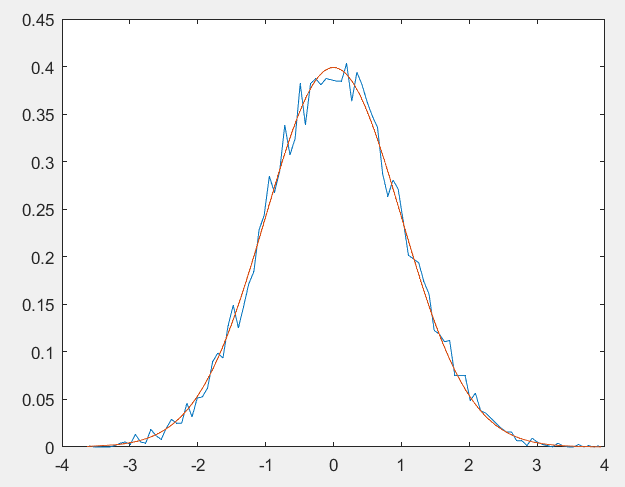
1.6两个方式的对比分析

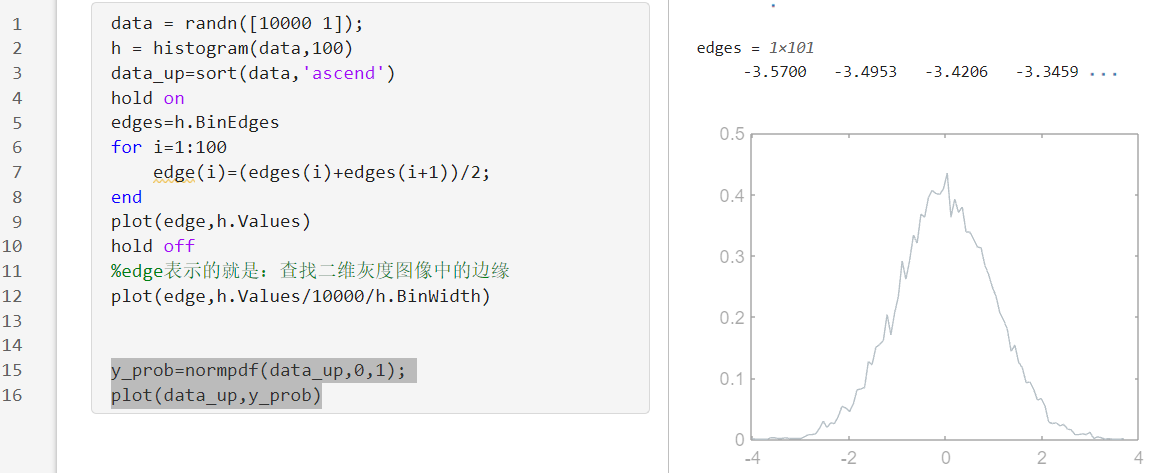
1）下面的这个图像是如何做到的，这个实际就是把两个图片显示在了一个画布上面罢了；

2）这个hold on表示的就是我们的这个图像在一个画布上面进行显示：因此我们生成上面的这个随机数据的函数图像之后，执行这个hold on命令（直接选中这个脚本里面的命令执行）然后再去执行这个下面的这个normodf函数去绘制这个图像，这样的话，两个图像就可以在一个画布上面进行显示了；

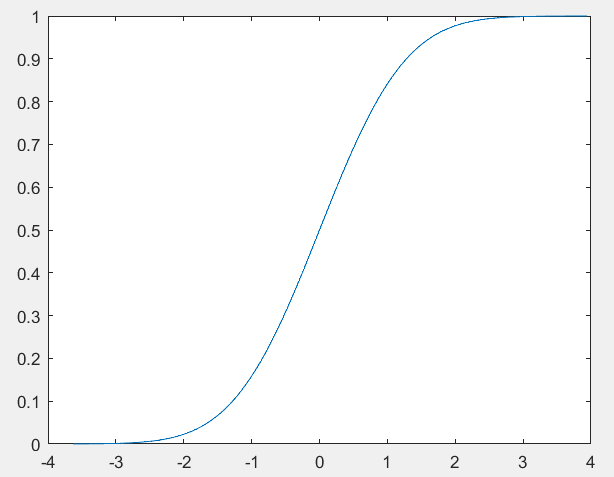
1.7分布函数

分布函数调用的也是我们的这个正态分布里面的函数normcdf函数，这个函数在我们的这个matlab里面的解释叫做累积密度函数，这个其实是一个意思，累积就是进行求解积分的嘛；

y_prob=normcdf(data_up,0,1);
plot(data_up,y_prob)

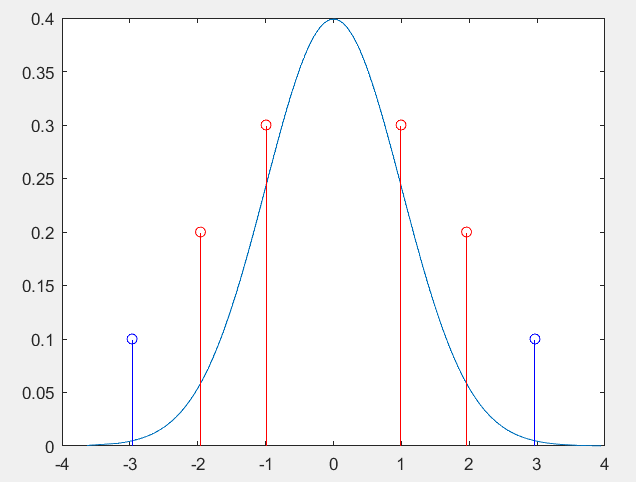
1.8分位数效果展示

下面的这个分位数的展示就是使用的我们的这三个对应的西格玛指标进行演示的；

stem里面的这个第二个参数表示我们的画的这个直线的高度，我们因为就是想要看到这个效果，因此这个包含的区间越大，这个时候和我们的这个已知图像的交点就会越低，这个时候我们的这个参数值调小就可以了；

y_prob=normpdf(data_up,0,1);
plot(data_up,y_prob)

y_prob=normcdf(data_up,0,1);
plot(data_up,y_prob)
%   68%-----95.4%-----99.7%
stem([norminv(0.025,0,1),norminv(0.975,0,1)],[.2,.2],'r')
stem([norminv(0.0015,0,1),norminv(0.9985,0,1)],[.1,.1],'b')
stem([norminv(0.16,0,1),norminv(0.84,0,1)],[.3,.3],'r')

原文地址：https://blog.csdn.net/binhyun/article/details/143756716

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！