【深度学习】Attention、Self-Attention、Multi-Head Attention
一、Attention
在CV领域,注意力机制通常分为通道注意力和空间注意力或者两者结合。
一张图像经backbone得到的特征通常包括多个通道,每个通道是一个像素矩阵,每个通道对任务的贡献不尽相同,单个通道的特征图中每个像素对任务的贡献也不尽相同。注意力机制就是希望通过加权的方式凸显其中重要的通道或像素。
1. SE
1.1 概念
Squeeze-and-Excitation Networks (SENet)是通道注意力的代表性工作,它为每个通道分配一个权重,其结构图如下:
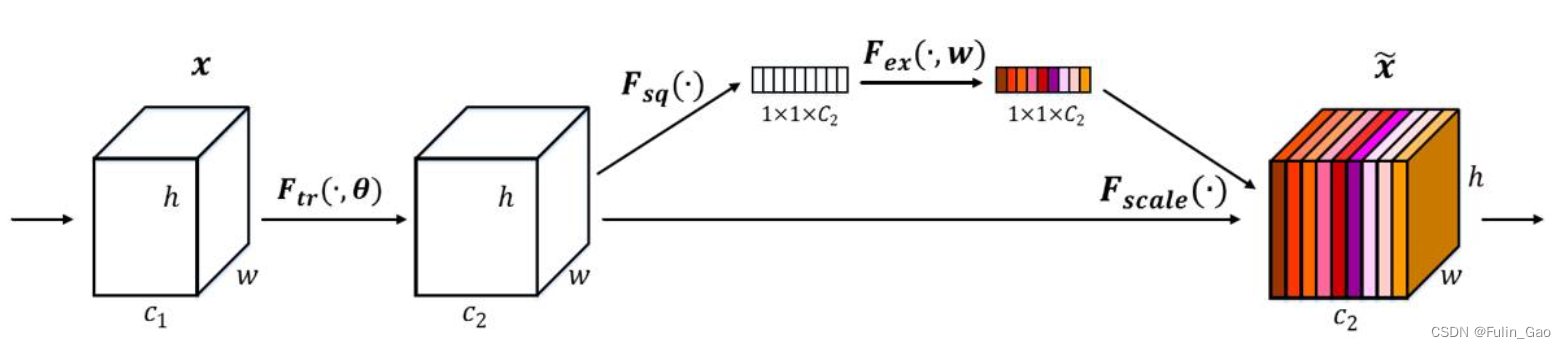
如图,
x
\boldsymbol{x}
x经
F
t
r
(
⋅
,
θ
)
F_{tr}(\cdot,\theta)
Ftr(⋅,θ)提取得到维度为
[
c
2
,
h
,
w
]
[c_2,h,w]
[c2,h,w]的特征,之后按照如下步骤获取各通道权重并完成加权:
(1) 对特征进行全局平均池化,每个通道都被池化为一个特征点,形成长度为
c
2
c_2
c2的特征向量。
(2) 经过两次全连接(两层的MLP),第一层神经元个数较少,第二层神经元个数为
c
2
c_2
c2。
(3) 第二层全连接输出经Sigmoid将值固定到0-1之间,即可得到分配给每个通道的权重。
(4) 将权重乘以对应通道的特征图。
1.2 实现
import torch
from torch import nn
class se_block(nn.Module):
def __init__(self, channel, ratio=16):
super().__init__()
self.avg_pool = nn.AdaptiveAvgPool2d((1, 1))
self.fc1 = nn.Linear(channel, channel // ratio, bias=False)
self.relu = nn.ReLU(inplace=True)
self.fc2 = nn.Linear(channel // ratio, channel, bias=False)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
w = self.avg_pool(x).squeeze(-1).squeeze(-1) # [8, 512, 24, 24] -> [8, 512, 1, 1] -> [8, 512, 1] -> [8, 512]
w = self.relu(self.fc1(w)) # [8, 512] -> [8, 32]
w = self.sigmoid(self.fc2(w)).unsqueeze(2).unsqueeze(3) # [8, 32] -> [8, 512] -> [8, 512, 1] -> [8, 512, 1, 1]
return w * x
if __name__ == "__main__":
x = torch.randn((8, 512, 24, 24))
se = se_block(512)
x_se = se(x)
2. ECA
2.1 概念
ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks也是一种通道注意力方法,对SENet做了改进。ECA认为通过全连接捕捉所有通道的信息是没有必要的,并且CNN具有良好的跨通道信息捕捉能力,于是ECA将两层全连接替换成了一层1D卷积。如下图,左图是SE模块,右图是ECA模块。
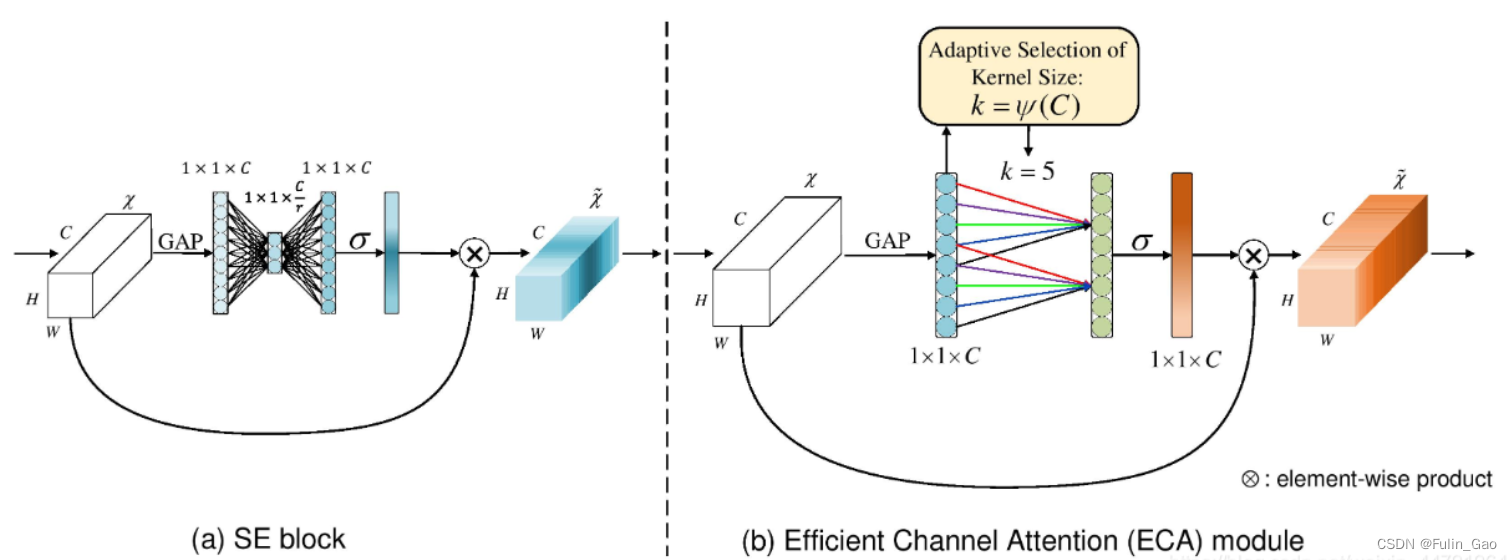
可以看出,将全连接替换为1D卷积后多了一个关键参数,即卷积核大小 k k k。ECA通过下式确定 k k k:
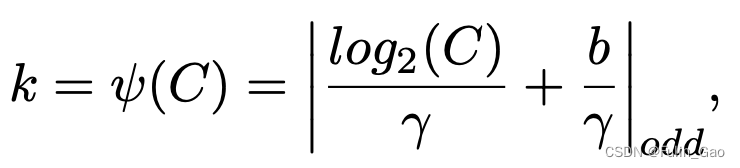
其中, C C C为通道数 , γ ,\gamma ,γ和 b b b是超参数,在ECA中被分别设为2和1, ∣ ⋅ ∣ o d d |\cdot|_{odd} ∣⋅∣odd表示取绝对值后再取最近的奇数。
2.2 实现
import math
import torch
from torch import nn
class eca_block(nn.Module):
def __init__(self, channel, gamma=2, b=1):
super().__init__()
self.avg_pool = nn.AdaptiveAvgPool2d((1, 1))
kernel_size = int(abs(math.log(channel, 2) / gamma + b / gamma))
kernel_size = kernel_size if kernel_size % 2 else kernel_size + 1 # 是奇数不变,是偶数+1
self.conv = nn.Conv1d(1, 1, kernel_size=kernel_size, padding=kernel_size // 2, bias=False) # 输入和输出通道数均为1,需要padding才能保证输出特征长度为channel
self.sigmoid = nn.Sigmoid()
def forward(self, x):
w = self.avg_pool(x).squeeze(-1).transpose(1, 2) # [8, 512, 24, 24] -> [8, 512, 1, 1] -> [8, 512, 1] -> [8, 1, 512]
w = self.sigmoid(self.conv(w)).transpose(1, 2).unsqueeze(-1) # [8, 1, 512] -> [8, 512, 1] -> [8, 512, 1, 1]
return w * x
if __name__ == "__main__":
x = torch.randn((8, 512, 24, 24))
eca = eca_block(512)
x_eca = eca(x)
3. CBAM
3.1 概念
CBAM: Convolutional Block Attention Module 结合了通道和空间注意力。
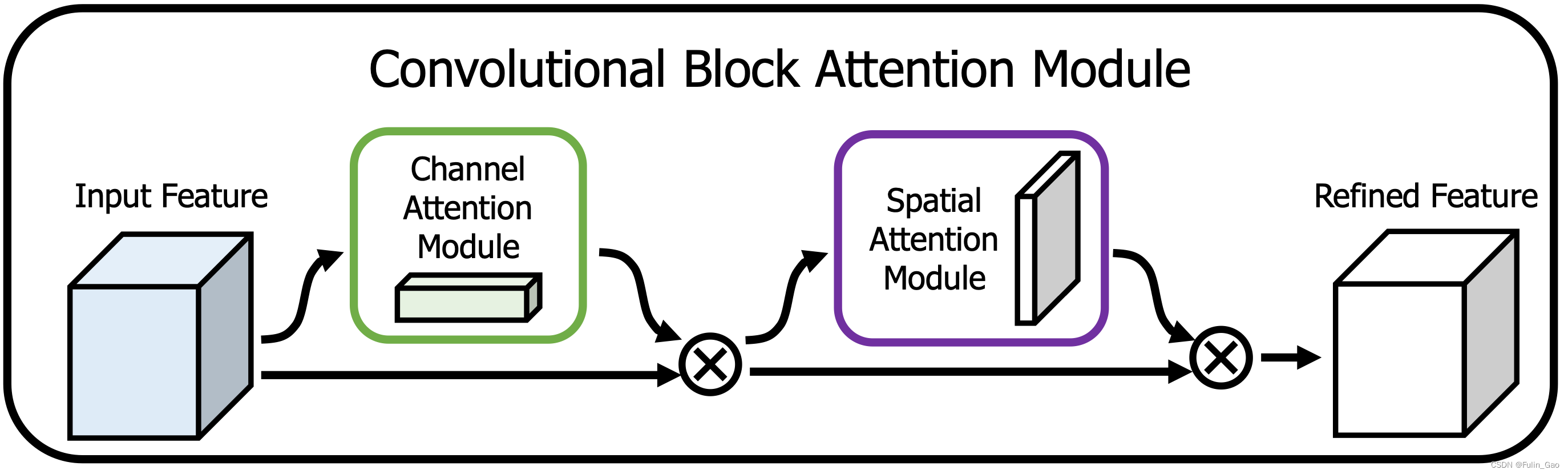
如图所示,CBAM先进行通道注意力然后再进行空间注意力。
对于通道注意力,其结构图如下:

可见,在通道注意力方面,CBAM与SE的差别为在池化时前者多了最大池化,于是在Sigmoid前两个池化向量经MLP的输出要先合并。
对于空间注意力,其结构图如下:
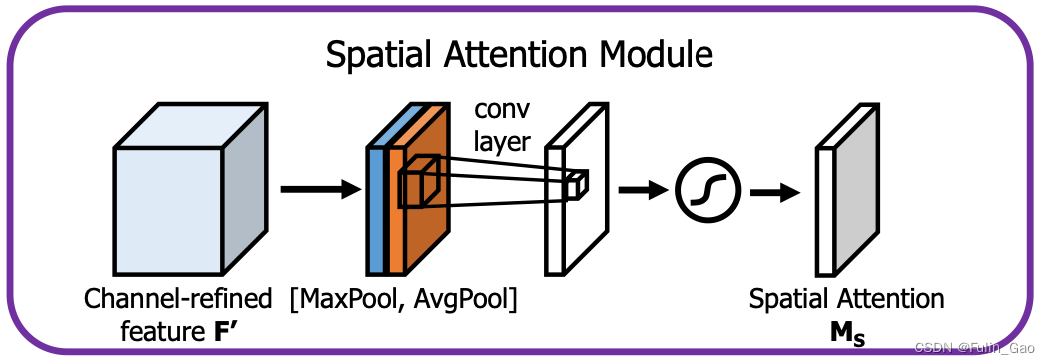
同样地,空间注意力部分也进行两种池化最大和平均,不过它不在通道尺度上进行,而是在特征图像素尺度上求所有通道的最大和平均。所以,池化后得到两个特征图(与输入的高宽一致),经过一个2D卷积核然后经Sigmoid即可得到在所有像素点上的权重。
3.2 实现
import torch
from torch import nn
class ChannelAttention(nn.Module):
def __init__(self, channel, ratio=16):
super(ChannelAttention, self).__init__()
self.avg_pool = nn.AdaptiveAvgPool2d((1, 1))
self.max_pool = nn.AdaptiveMaxPool2d((1, 1))
self.fc1 = nn.Conv2d(channel, channel // ratio, kernel_size=1, bias=False) # 使用1*1卷积代替全连接,参数量相同,但是输入和输出维度不需要转换了
self.relu = nn.ReLU(inplace=True)
self.fc2 = nn.Conv2d(channel // ratio, channel, kernel_size=1, bias=False)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
w_m = self.max_pool(x)
w_a = self.avg_pool(x)
w_m = self.relu(self.fc1(w_m))
w_a = self.relu(self.fc1(w_a))
w = self.sigmoid(self.fc2(w_m) + self.fc2(w_a))
return w * x
class SpatialAttention(nn.Module):
def __init__(self, kernel_size=7):
super(SpatialAttention, self).__init__()
self.conv = nn.Conv2d(2, 1, kernel_size=kernel_size, padding=kernel_size // 2, bias=False) # 原文kernel_size=7
self.sigmoid = nn.Sigmoid()
def forward(self, x):
w_m, _ = torch.max(x, dim=1, keepdim=True)
w_a = torch.mean(x, dim=1, keepdim=True)
w = torch.cat([w_m, w_a], dim=1) # 两个[8, 1, 24, 24]拼接为一个[8, 2, 24, 24]
w = self.sigmoid(self.conv(w))
return w * x
class cbam(nn.Module):
def __init__(self, channel):
super(cbam, self).__init__()
self.channel_attention = ChannelAttention(channel)
self.spatial_attention = SpatialAttention()
def forward(self, x):
x = self.channel_attention(x)
x = self.spatial_attention(x)
return x
if __name__ == "__main__":
x = torch.randn((8, 512, 24, 24))
cbam = cbam(512)
x_cbam = cbam(x)
二、Self-Attention
自注意力最先在NLP领域被提出,后来被用到CV领域。自注意力也是注意力的一种,本质上也是对原特征进行加权。“自”体现在它的权重不是像上面的方法通过网络学习出来,而是根据自身特征计算而来。
1. 概念
首先,我们以NLP中的数据形式理解Self-Attention,NLP中一个批次的数据包括多个句子,每个句子有多个单词,每个单词通过某种转换可以形成固定长度的特征向量,又称embedding。于是一个句子就被转换为大小为 [ L , C ] [L,C] [L,C]的特征矩阵 X X X, L L L为该句子中单词的个数, C C C是embedding的长度。
对于一个句子的特征矩阵,自注意力的关键公式如下:

其中, Q , K , V Q,K,V Q,K,V为 X X X分别经过线性变化得到的特征矩阵, d k d_k dk为 K K K中特征向量的长度(一般与embedding的长度一致)。
但是,直接从 Q , K , V Q,K,V Q,K,V讲起理解较为困难,为进一步体现“自”的含义,我们简化上式,从下式开始讲起:
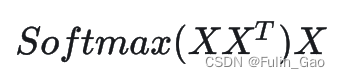
其中, X X T XX^T XXT是 X X X中embedding两两之间的点积,从几何上理解点积是一个向量在另一个向量上的投影,能够衡量两个向量在方向和长度上的相似度。
所以 X X T XX^T XXT是一个相似度矩阵,经过SoftMax之后,相似度被归一化至 [ 0 , 1 ] [0,1] [0,1],变得更适合用来加权。可以理解为 S o f t M a x ( X X T ) SoftMax(XX^T) SoftMax(XXT)是一个权重矩阵,用来加权 X X X。 S o f t M a x ( X X T ) X SoftMax(XX^T)X SoftMax(XXT)X与 X X X的尺寸是一致的,它的每一行都是 X X X中各行的加权和,对应的权重是 X X X中当前行与各行的点积相似度。
可以看出,上述操作是通过自身获取权重再加权自身,这就是“自”的含义。
然后,我们对比上面两个图像中的公式,可以发现,区别如下有两个部分:
(1)
区别: 前者是
Q
,
K
,
V
Q,K,V
Q,K,V,后者是
X
X
X。
解释:
Q
,
K
,
V
Q,K,V
Q,K,V是
X
X
X分别经过线性变化得到的特征,通常是通过三个全连接层分别进行变换,这样做能够从一定程度上提升Self-Attention的效果,毕竟多了三个可学习的参数矩阵。
(2)
区别: 前者多了一个
1
d
k
\frac{1}{\sqrt{d_k}}
dk1,
d
k
d_k
dk为
K
K
K中特征向量的长度。
解释: 如果
Q
Q
Q和
K
K
K的特征长度很长(
Q
Q
Q和
K
K
K的长度可以与
X
X
X不同,但一般是相同的),就会导致
Q
K
T
QK^T
QKT的值很大,使得
S
o
f
t
M
a
x
SoftMax
SoftMax的梯度消失,除以
d
k
\sqrt{d_k}
dk能够避免该问题。
2. 实现
import torch.nn as nn
import torch
import math
class SelfAttention(nn.Module):
def __init__(self, dim_in, dim_k, dim_v):
super(SelfAttention, self).__init__()
self.dim_in = dim_in
self.dim_k = dim_k # K与Q的特征长度相同,可以与V的特征长度不同
self.dim_v = dim_v # V可以与输入特征长度不同,但为了即插即用,通常dim_in=dim_v
self.linear_q = nn.Linear(dim_in, dim_k, bias=False)
self.linear_k = nn.Linear(dim_in, dim_k, bias=False)
self.linear_v = nn.Linear(dim_in, dim_v, bias=False)
self.scale = 1 / math.sqrt(dim_k)
def forward(self, x):
q = self.linear_q(x) # [batch_size, n, dim_in] -> [batch_size, n, dim_k]
k = self.linear_k(x) # [batch_size, n, dim_in] -> [batch_size, n, dim_k]
v = self.linear_v(x) # [batch_size, n, dim_in] -> [batch_size, n, dim_v]
w = torch.bmm(q, k.transpose(1, 2)) * self.scale # (QK^T)/sqrt(dim_k)
w = torch.softmax(w, dim=-1) # SoftMax[(QK^T)/sqrt(dim_k)]
att = torch.bmm(w, v) # SoftMax[(QK^T)/sqrt(dim_k)]V
return att
if __name__ == "__main__":
x = torch.randn((8, 6, 512))
self_attention = SelfAttention(512, 128, 512)
o = self_attention(x)
三、Multi-Head Attention
上述只进行一次自注意力计算的情况称为单头自注意力,与之相对的,多头自注意力会将 Q , K , V Q,K,V Q,K,V进行拆分(拆成几份就是几个头),然后分别进行自注意力计算,最后将各部分计算结果拼接并通过一次仿射变换得到新的输出。
使用多个头能从不同层面(representation subspace)考虑相似性,提供模型表达能力。
1. 概念
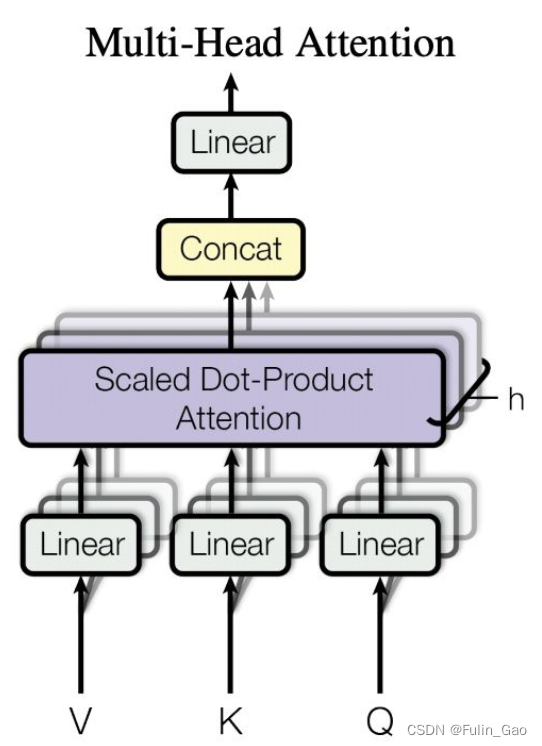
如上图,我们将图中与 Q , K , V Q,K,V Q,K,V相连的 L i n e a r Linear Linear视为拆分操作,假设 Q , K , V Q,K,V Q,K,V大小均为 [ 6 , 512 ] [6,512] [6,512],头的数量为4(必须是能整除embedding长度512的),那么拆分后就有4组大小均为 [ 6 , 128 ] [6,128] [6,128]的 q , k , v q,k,v q,k,v。对同组的 q , k , v q,k,v q,k,v进行Self-Attention计算(对应图中Scaled Dot-Product Attention)会得到4组大小均为 [ 6 , 128 ] [6,128] [6,128]的输出,拼接起来就得到大小为 [ 6 , 512 ] [6,512] [6,512]的输出。最后经过一层全连接进行仿射变换即可得到Multi-Head Attention的输出。
2. 实现
import math
import torch
import torch.nn as nn
class MultiHeadAttention(nn.Module):
def __init__(self, dim_in, dim_k, dim_v, num_heads=4):
super(MultiHeadAttention, self).__init__()
assert dim_k % num_heads == 0 and dim_v % num_heads == 0, "dim_k and dim_v must be multiple of num_heads"
self.num_heads = num_heads
self.dim_in = dim_in
self.dim_k = dim_k
self.dim_v = dim_v
self.scale = 1 / math.sqrt(dim_k / num_heads)
self.linear_q = nn.Linear(dim_in, dim_k)
self.linear_k = nn.Linear(dim_in, dim_k)
self.linear_v = nn.Linear(dim_in, dim_v)
self.fc = nn.Linear(dim_v, dim_v)
def forward(self, x):
batch_size, n, dim_in = x.shape
Q = self.linear_q(x) # [batch_size, n, dim_in] -> [batch_size, n, dim_k]
K = self.linear_k(x) # [batch_size, n, dim_in] -> [batch_size, n, dim_k]
V = self.linear_v(x) # [batch_size, n, dim_in] -> [batch_size, n, dim_v]
nh = self.num_heads
dk = self.dim_k // nh # 每个头的k的长度,使用 // 可以确保得到的是整数
dv = self.dim_v // nh # 每个头的v的长度
# 将头的位置放在第2个,这样后面计算点积时就是每个头单独计算
q = Q.reshape(batch_size, n, nh, dk).transpose(1, 2) # [batch_size, n, dim_k] -> [batch_size, n, num_heads, dk] -> [batch_size, num_heads, n, dk]
k = K.reshape(batch_size, n, nh, dk).transpose(1, 2) # [batch_size, n, dim_k] -> [batch_size, n, num_heads, dk] -> [batch_size, num_heads, n, dk]
v = V.reshape(batch_size, n, nh, dv).transpose(1, 2) # [batch_size, n, dim_v] -> [batch_size, n, num_heads, dv] -> [batch_size, num_heads, n, dv]
w = torch.matmul(q, k.transpose(2, 3)) * self.scale # (qk^T)/sqrt(dk)
w = torch.softmax(w, dim=-1) # SoftMax[(qk^T)/sqrt(dk)]
att = torch.matmul(w, v) # SoftMax[(qk^T)/sqrt(dk)]v
att = att.transpose(1, 2).reshape(batch_size, n, self.dim_v) # [batch_size, num_heads, n, dv] -> [batch_size, n, num_heads, dv] -> [batch_size, n, dim_v]
att = self.fc(att) # [batch_size, n, dim_v] -> [batch_size, n, dim_v]
return att
if __name__ == '__main__':
x = torch.randn((8, 6, 512))
mh_attention = MultiHeadAttention(512, 512, 512)
o = mh_attention(x)
致谢:
本博客仅做记录使用,无任何商业用途,参考内容如下:
神经网络学习小记录64——Pytorch 图像处理中注意力机制的解析与代码详解
self-Attention|自注意力机制 |位置编码 | 理论 + 代码
SE、CBAM、ECA注意力机制
原文地址:https://blog.csdn.net/beginner1207/article/details/137874996
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
