scipy.signal.cwt 与 pywt.cwt 使用记录

scipy.signal.cwt

该代码中widths以及freq计算公式来源于scipy.signal.morlet2函数官方案例

from scipy.signal import morlet, morlet2
from scipy import signal
import matplotlib.pyplot as plt

signal_length = 2000
fs = 1000

# 生成信号数据
time = np.arange(0, signal_length) / fs
signal_data = np.zeros_like(time)
tt = time <= 0.5
signal_data[tt] = np.sin(2 * np.pi * 300 * time[tt])
tt = time > 0.5
signal_data[tt] = np.sin(2 * np.pi * 300 * time[tt]) + np.sin(2 * np.pi * 50 * time[tt])
tt = time > 1.5
signal_data[tt] = signal_data[tt] + np.sin(2 * np.pi * 400 * time[tt])

wavelet = 'morl'
totalscal = 64

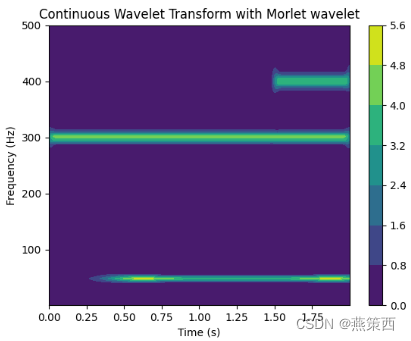
# # # 使用signal.cwt对signal_data进行分析
# widths = np.arange(1, totalscal)
fc = 50.  # fc=40~60 better
freq = np.linspace(1, fs / 2, totalscal)
widths = fc * fs / (2 * freq * np.pi)

cwtmatr = signal.cwt(signal_data, morlet2, widths, w=fc)
ic(abs(cwtmatr).shape)

plt.contourf(time, freq, abs(cwtmatr))
plt.colorbar()
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.title('Continuous Wavelet Transform with Morlet wavelet')
plt.show()

pywt.cwt

import pywt
import matplotlib.pyplot as plt

signal_length = 2000
fs = 1000

# 生成信号数据
time = np.arange(0, signal_length) / fs
signal_data = np.zeros_like(time)
tt = time <= 0.5
signal_data[tt] = np.sin(2 * np.pi * 300 * time[tt])
tt = time > 0.5
signal_data[tt] = np.sin(2 * np.pi * 300 * time[tt]) + np.sin(2 * np.pi * 50 * time[tt])
tt = time > 1.5
signal_data[tt] = signal_data[tt] + np.sin(2 * np.pi * 400 * time[tt])

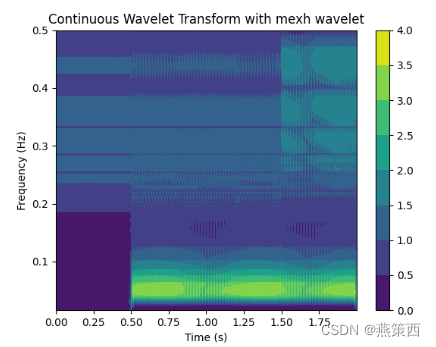
totalscal = 64
wavelet = 'mexh'

# ic(pywt.wavelist())
fc = pywt.central_frequency(wavelet, precision=10)
scales = 2 * fc * totalscal / np.arange(totalscal, 1, -1)

coeffs, freqs = pywt.cwt(signal_data, scales, wavelet)
cs = plt.contourf(time, freqs, abs(coeffs))  # , cmap='jet'
plt.colorbar()
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.title(f'Continuous Wavelet Transform with {wavelet} wavelet')
plt.show()

下列代码源于pywt官网案例：https://pywavelets.readthedocs.io/en/latest/ref/cwt.html

import pywt
import matplotlib.pyplot as plt

signal_length = 2000
fs = 1000

# -------------
# 生成信号数据
time = np.arange(0, signal_length) / fs
signal_data = np.zeros_like(time)
tt = time <= 0.5
signal_data[tt] = np.sin(2 * np.pi * 300 * time[tt])
tt = time > 0.5
signal_data[tt] = np.sin(2 * np.pi * 300 * time[tt]) + np.sin(2 * np.pi * 50 * time[tt])
tt = time > 1.5
signal_data[tt] = signal_data[tt] + np.sin(2 * np.pi * 400 * time[tt])

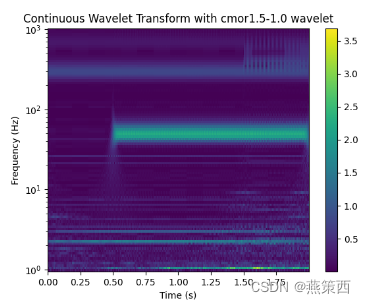
wavelet = 'cmor1.5-1.0'
# ic(pywt.wavelist())
coeffs, freqs = pywt.cwt(signal_data, np.geomspace(1, 1024, num=100),
                         wavelet, sampling_period=1 / fs)

plt.pcolormesh(time, freqs, np.abs(coeffs))
ax = plt.gca()
ax.set_yscale('log')

plt.colorbar()
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.title(f'Continuous Wavelet Transform with {wavelet} wavelet')
plt.show()

原文地址：https://blog.csdn.net/weixin_43543177/article/details/137715121

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！