C#，最小生成树（MST）克鲁斯卡尔（Kruskal）算法的源代码

一、Kruskal算法简史

克鲁斯卡尔（Kruskal）算法是一种用来寻找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。

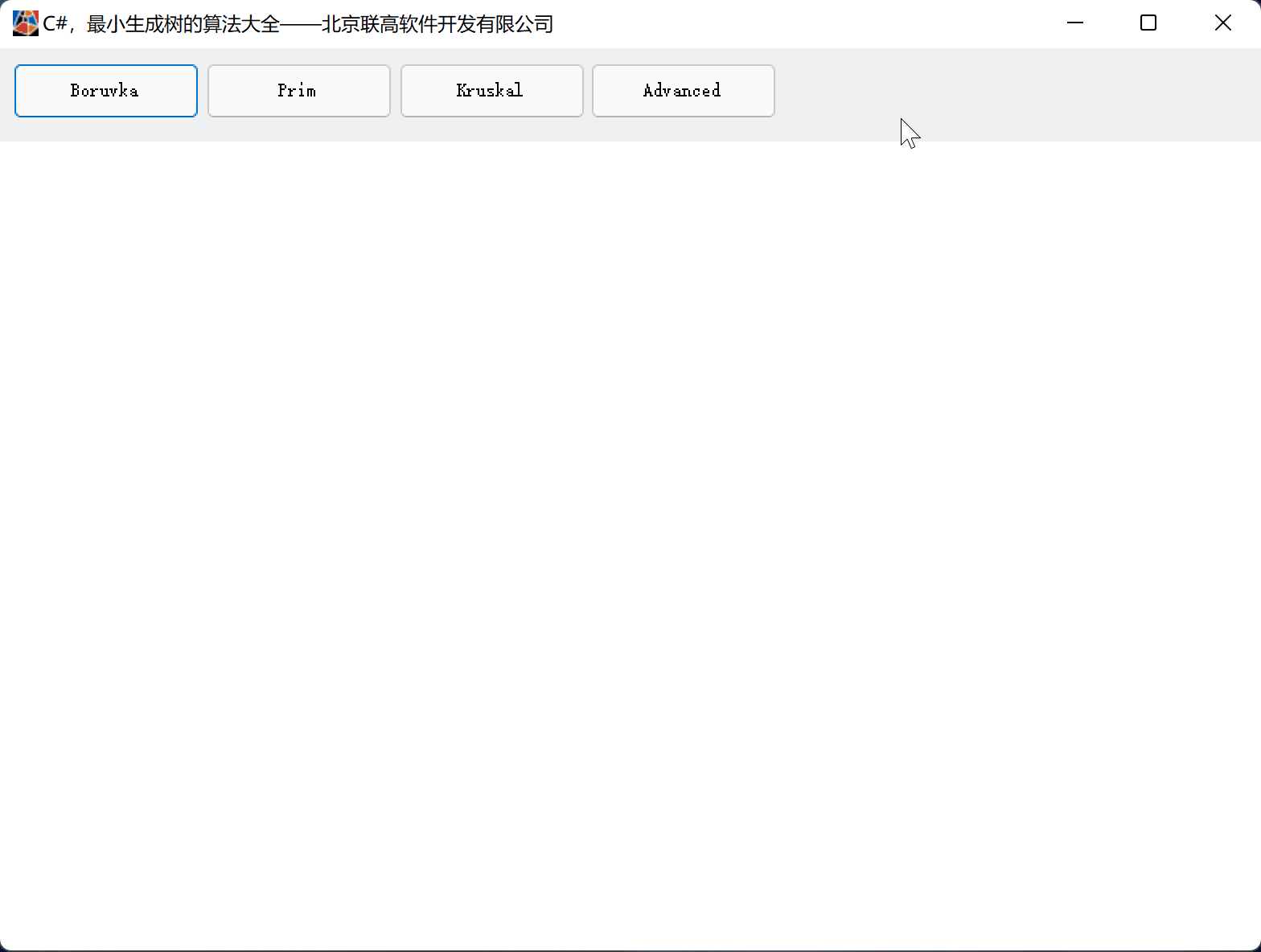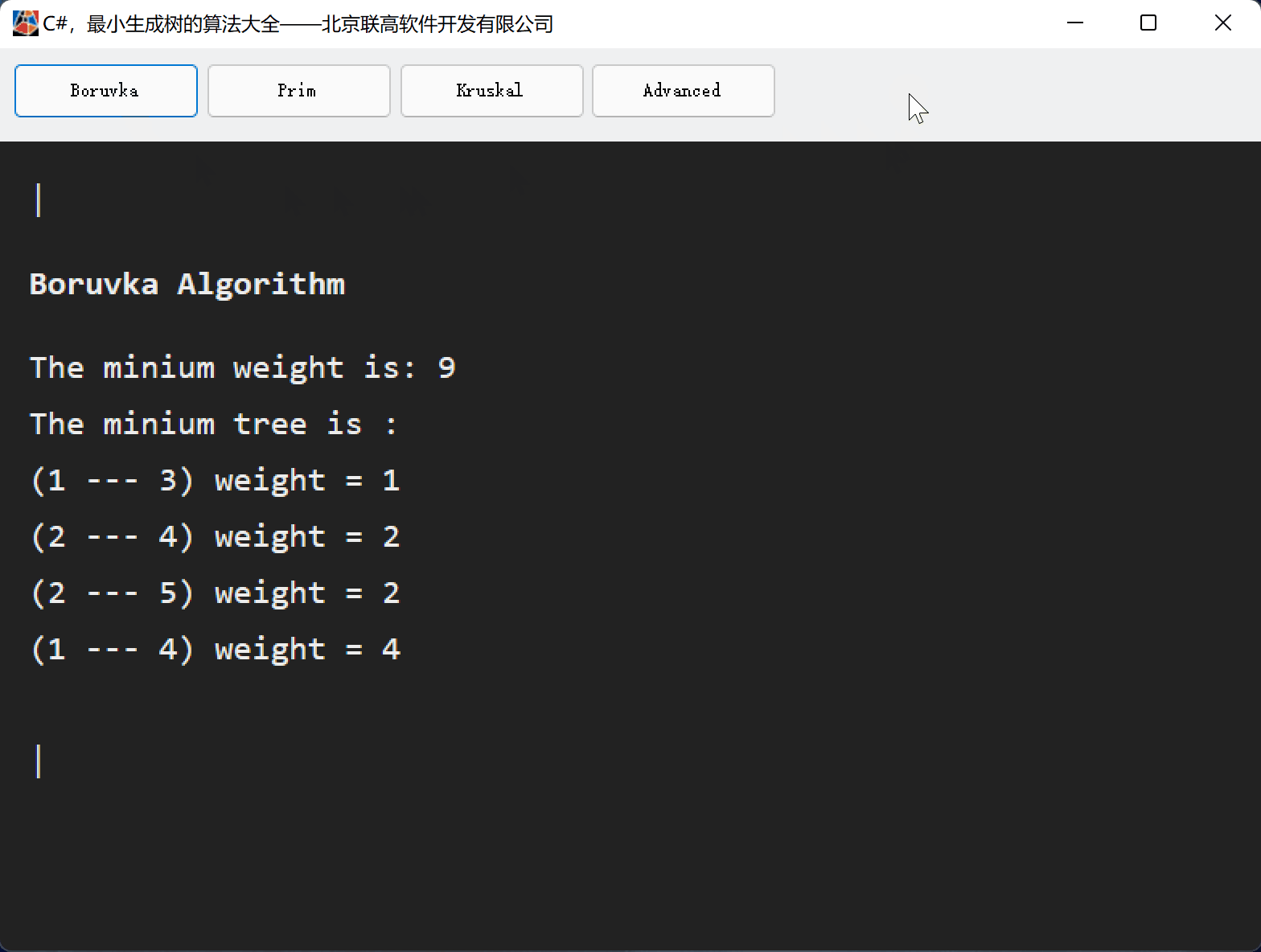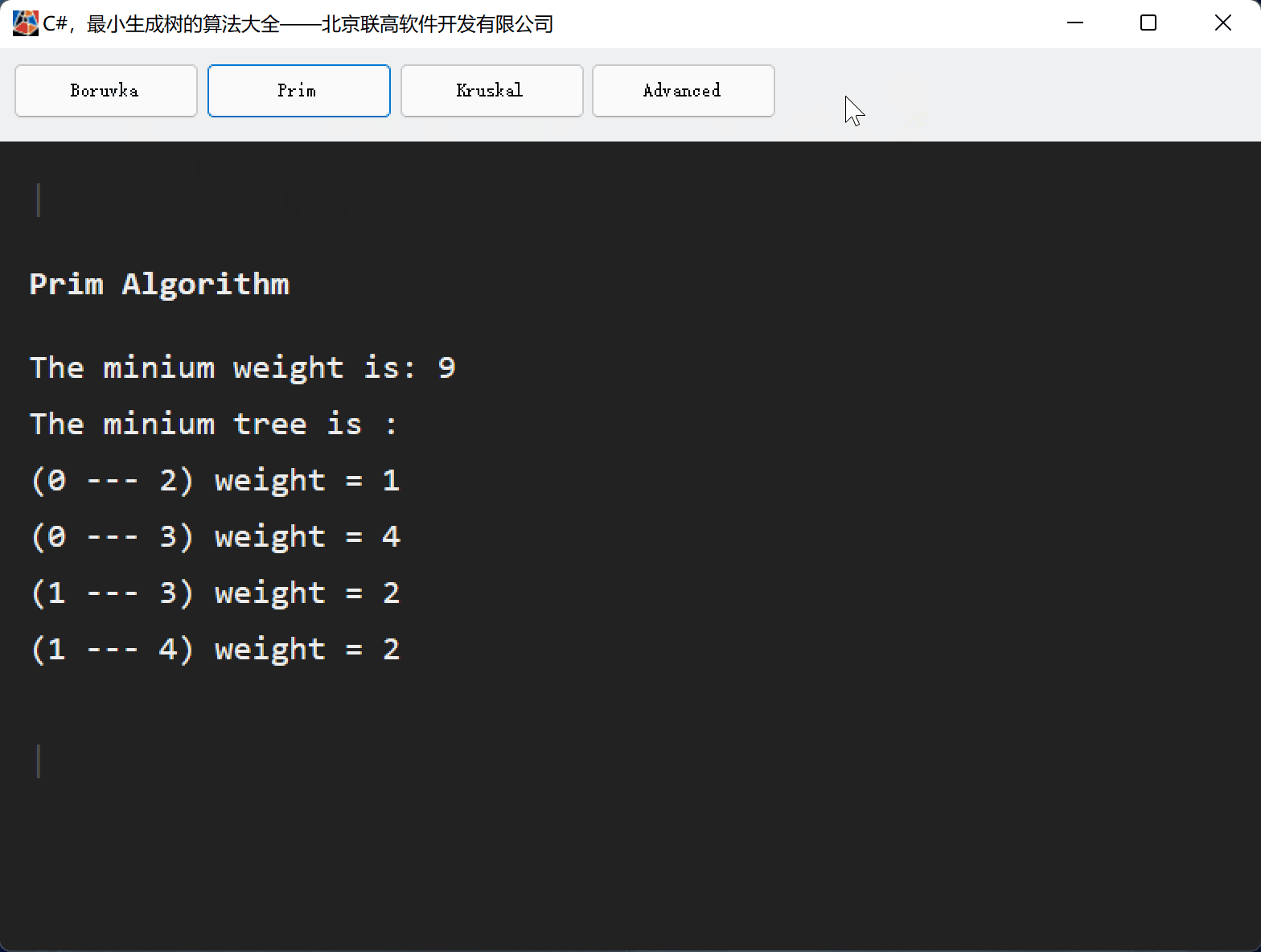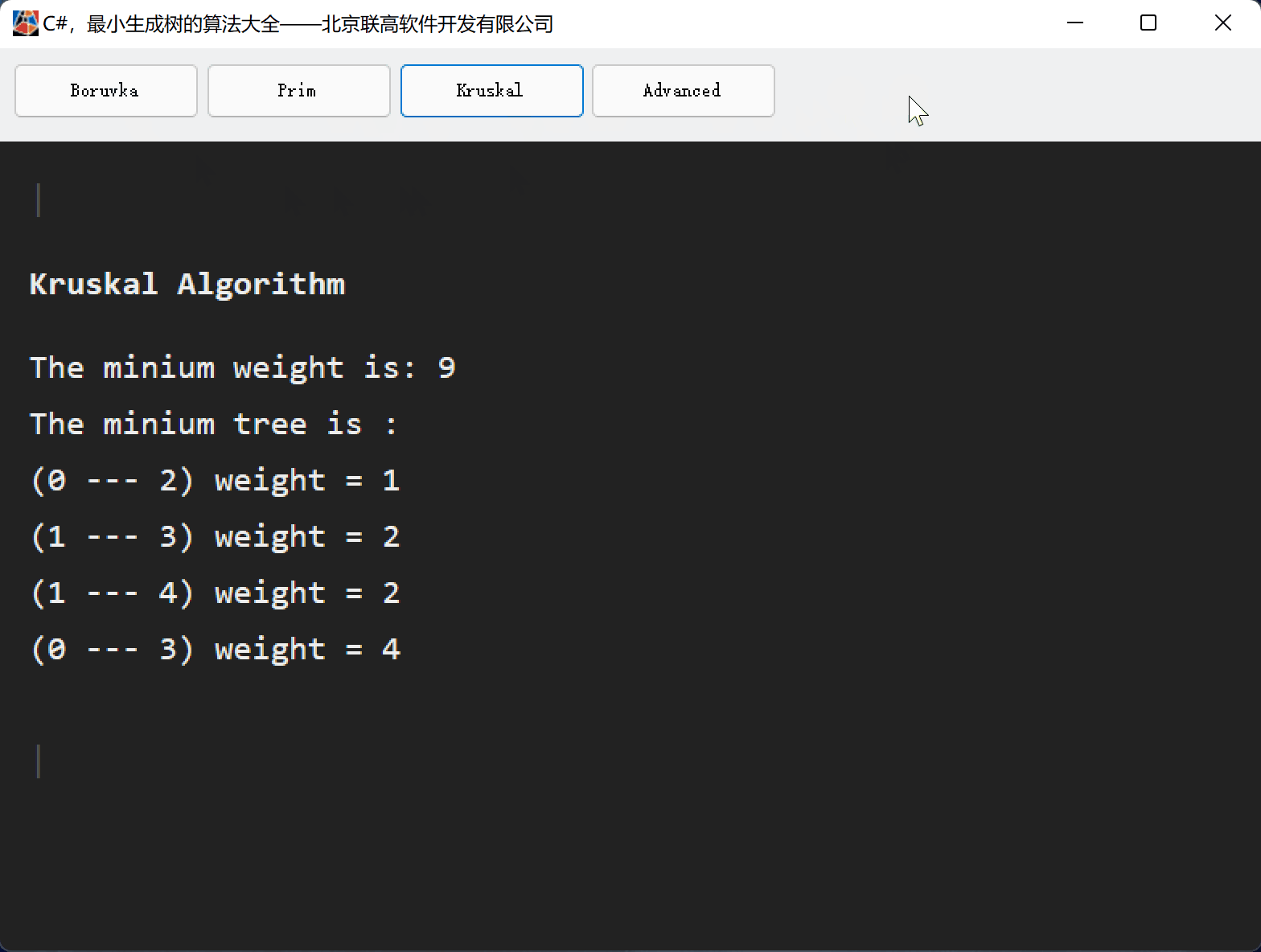
二、Kruskal算法思路

（1）记Graph中有v个顶点，e个边；
（2）新建图，拥有原图中相同的e个顶点，但没有边；
（3）将原图中所有e个边按权值从小到大排序；
（4）循环：从权值最小的边开始遍历每条边，直至图中所有的节点都在同一个连通分量中。
如果这条边连接的两个节点于图中不在同一个连通分量中，添加这条边到图中。如此反复。

三、Kruskal算法的源代码

核心代码：

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
public class Subset
{
public int Parent { get; set; } = 0;
public int Rank { get; set; } = 0;
}

/// <summary>
/// 最小生成树 Kruskal 算法
/// </summary>
public static class MST_Kruskal_Algorithm
{
private static int Find(Subset[] subsets, int i)
{
if (subsets[i].Parent != i)
{
subsets[i].Parent = Find(subsets, subsets[i].Parent);
}
return subsets[i].Parent;
}

private static void Union(Subset[] subsets, int x, int y)
{
int xroot = Find(subsets, x);
int yroot = Find(subsets, y);

            if (subsets[xroot].Rank < subsets[yroot].Rank)
{
subsets[xroot].Parent = yroot;
}
else if (subsets[xroot].Rank > subsets[yroot].Rank)
{
subsets[yroot].Parent = xroot;
}
else
{
subsets[yroot].Parent = xroot;
subsets[xroot].Rank++;
}
}

public static int Execute(Undirected_Graph graph, out List<WeightEdge> tree)
{
tree = new List<WeightEdge>();
int Vertex_Number = graph.Vertex_Number;

WeightEdge[] result = new WeightEdge[Vertex_Number];
int e = 0;
int i = 0;
for (i = 0; i < Vertex_Number; ++i)
{
result[i] = new WeightEdge();
}

graph.EdgeArray.Sort(delegate(WeightEdge a, WeightEdge b) { 
return a.CompareTo(b); 
});

Subset[] subsets = new Subset[Vertex_Number];
for (i = 0; i < Vertex_Number; ++i)
{
subsets[i] = new Subset();
}

for (int v = 0; v < Vertex_Number; ++v)
{
subsets[v].Parent = v;
subsets[v].Rank = 0;
}

i = 0;
while (e < (Vertex_Number - 1))
{
WeightEdge next_edge = graph.EdgeArray[i++];

int x = Find(subsets, next_edge.Start);
int y = Find(subsets, next_edge.End);

if (x != y)
{
result[e++] = next_edge;
Union(subsets, x, y);
}
}

int minimumCost = 0;
for (i = 0; i < e; ++i)
{
tree.Add(new WeightEdge(result[i].Start,result[i].End, result[i].Weight));
minimumCost += result[i].Weight;
}
return minimumCost;
}
}
}

 ——————————————————————

POWER BY 315SOFT.COM &
TRUFFER.CN

原文地址：https://blog.csdn.net/beijinghorn/article/details/124270819

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！