[USACO1.5] 八皇后 Checker Challenge

题目描述

检查一个如下的6 x 6的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行，每列，每条对角线(包括两条主对角线的所有对角线)上都至多有一个棋子，如下例，就是一种正确的布局。

上面的布局可以用序列2 4 6 1 3 5来描述，第i个数字表示在第i行的相应位置有一个棋子，如下：
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
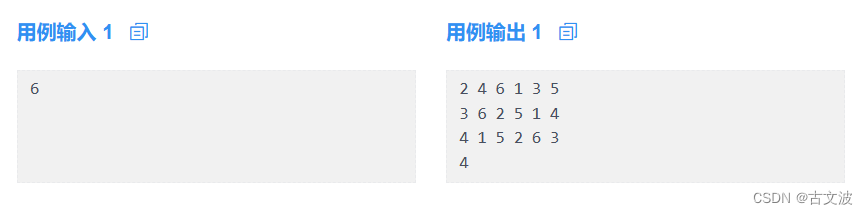
这只是跳棋放置的一个解。请写一个程序找出所有跳棋放置的解，并把它们以上面的序列方法输出。解按字典顺序排列，请输出前3个解，最后一行是解的总个数。

输入描述

一个数字N (6<=N<=14) 表示棋盘是N x N大小的。

输出描述

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

提示

【数据范围】
对于100% 的数据，6≤n≤13。
USACO Training Section 1.5

思路：

我们要使用回溯算法。

定义4个数组：a,b,c,d
用a数组来存储列号
接下来，我们用b，c，d来判断该位置是否可以放皇后

参考代码

#include <bits/stdc++.h>

using namespace std;

const int N = 107;

int n, ans; // 棋盘大小和答案
int a[N], b[N], c[N], s[N]; // 标记

void print_ans() { // 用来输出答案
if(ans < 3) { // 只有第1-3个解才输出
    for(int i = 1; i <= n; i++)
        cout << s[i] << ' '; // 输出列数
cout << endl; // 要换行
    }
    ans++; // 因为这是一种方法，所以加一次方案数
}

void dfs(int i) {
if(i > n) { // 如果方案可以
    print_ans(); // 进行操作
        return; // 必须要加，否则无法退出
    }
    for(int j = 1; j <= n; j++)
        {
            if((!a[j]) && (!b[i + j]) && (!c[i - j + n])) // 判断该方法是否可行
            {
                s[i] = j;
                a[j] = 1;
                b[i + j] = 1;
                c[i - j + n] = 1; // 标记上下斜的地方不能放了
                dfs(i + 1); // 继续往下查找
                a[j] = 0; // 查找完后返回，相当于并没有实际走，重新标记为可走
                b[i + j] = 0;
                c[i - j + n] = 0;
            }
        }
}

int main() {
cin >> n;
    dfs(1); // 寻找方案数
    cout << ans; // void型函数不输出，所以用ans统计答案
    return 0;
}

原文地址：https://blog.csdn.net/C13256134687/article/details/138022244

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！