开源音乐分离器Audio Decomposition:可实现盲源音频分离,无需外部乐器分离库,从头开始制作。将音乐转换为五线谱的程序
今天给大家分析一个音频分解器,通过傅里叶变换和信封匹配分离音乐中的各个音符和乐器,实现音乐到乐谱的转换。将音乐开源分离为组成乐器。该方式是盲源分离,从头开始制作,无需外部乐器分离库。
相关链接
代码:https://github.com/mbird1258/Audio-Decomposition
演示视频:https://youtu.be/-i0PSxcoDH0

准备
仪器数据
乐器数据全部来自爱荷华大学电子音乐工作室乐器数据库。利用这些文件,我们用下文所述方法找到整个波的傅里叶变换和波的包络。
工作原理
乐器的声波主要由其傅里叶变换和包络线来表征。因此,我们可以利用这两者来很好地了解哪种乐器正在演奏哪个音符。

傅立叶变换
该程序将音乐分解为组成音符和乐器的第一种方法是每 0.1 秒对音乐文件进行一次傅里叶变换(频谱图),并将我们存储的每种乐器的傅里叶变换相加,以重新创建 0.1 秒窗口的傅里叶变换。这个想法是希望在设定的时间内完美地重现音乐,因为傅里叶变换应该能相对好地代表所演奏的音乐。
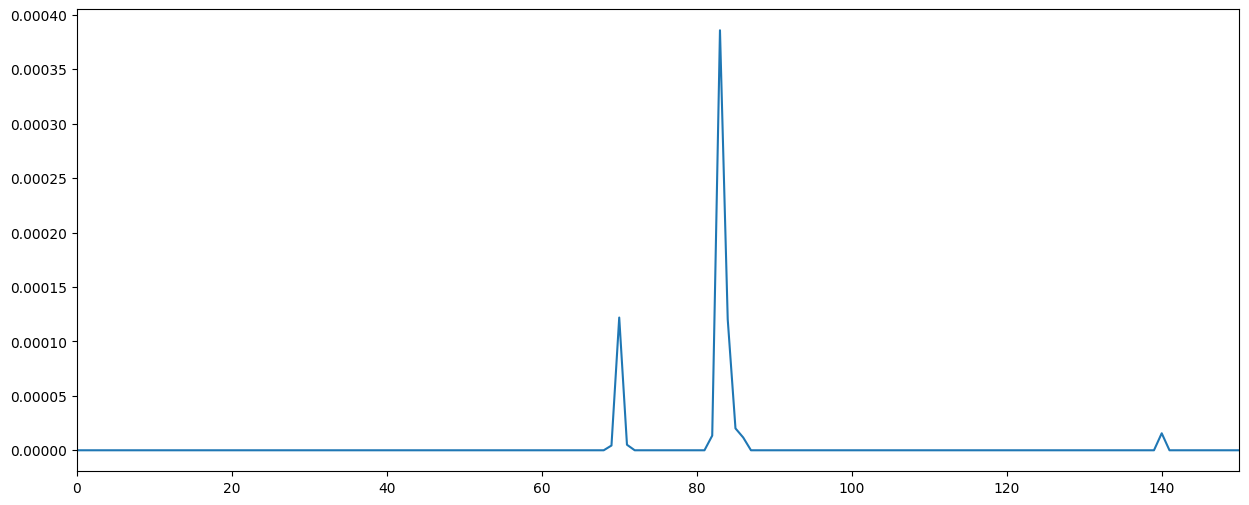
原始傅里叶变换
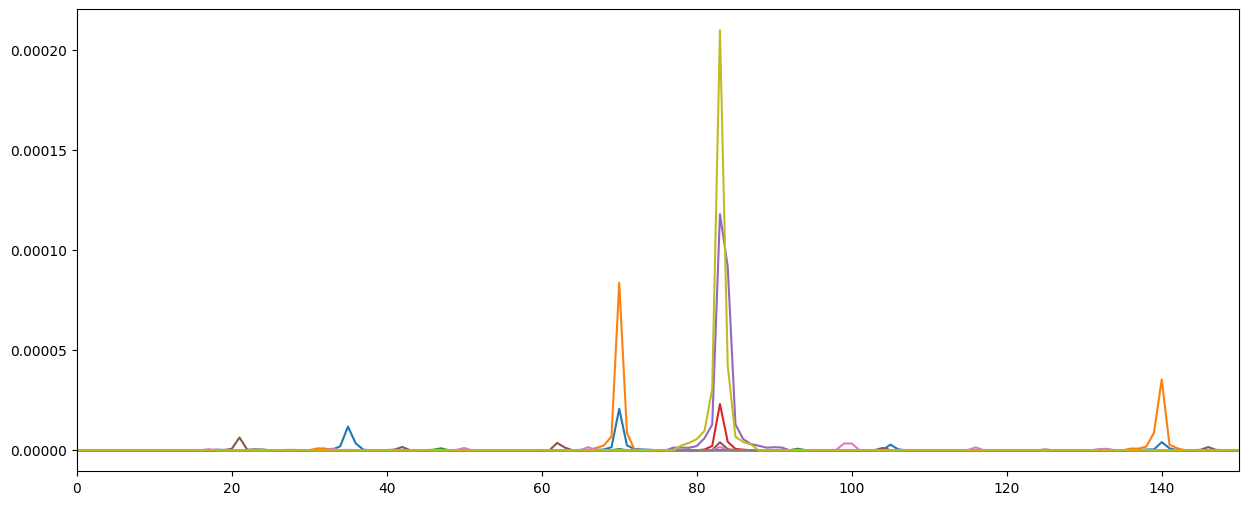
组成文书
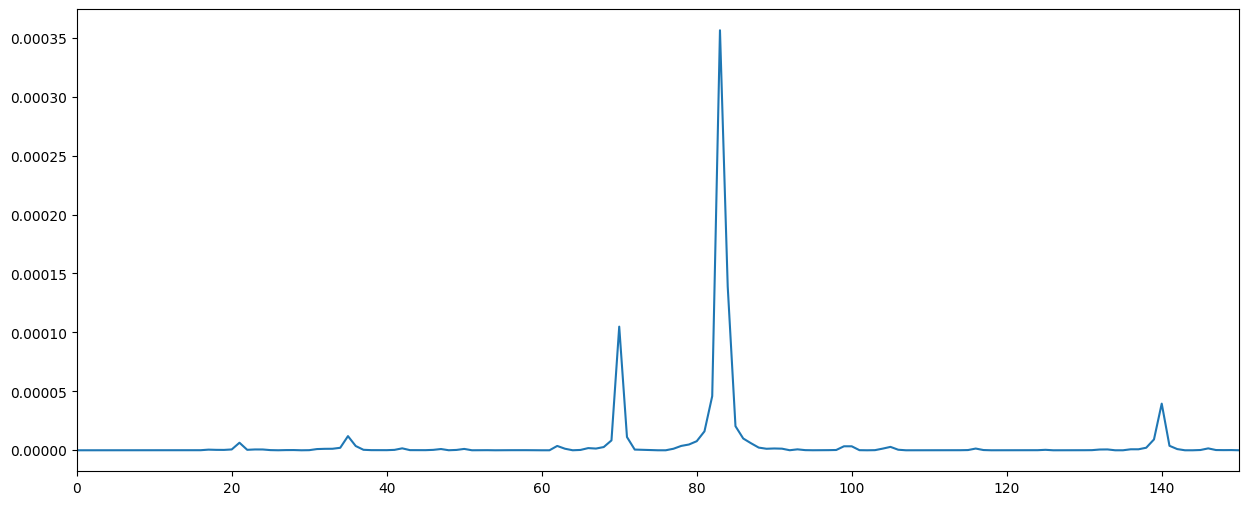
通过求解以下矩阵可得出每种乐器的幅度。该矩阵是通过对每种乐器的 MSE 成本函数按频率(例如 5 hz 时的 FT 值)求偏导数而得出的。矩阵中的每一行都是不同的偏导数。(第一个是相对于大提琴的,第二个是相对于钢琴的,等等)

信封
将乐器的包络与声波匹配的第一步是获取包络本身。包络是波的上限,虽然有函数可以做到这一点,但它们似乎难以处理噪音和某些类型的声波。因此,由于我们必须处理不同频率的许多不同乐器,我们需要一个更强大的解决方案。
为了获得包络,该函数将声波分成几块,然后取每块的最大值。为了进一步优化结果,该函数找到包络低于原始声波的点,并添加一个定义包络的新点。

下一步是将波的包络分解为起音、延音和释音。起音是音符的初始噪音,延音是音符保持时,释音是音符停止时。对于乐器样本,我们可以取波的第一个非零值来获取起音的开始。要获取起音和延音之间的点,我们获取函数向下凹或减小时的第一个点。要获取延音和释音之间的点,我们获取函数增加或向下凹的末端的第一个点。要获取释音的末端,我们找到函数非零的末端的第一个点。
为了进一步对波进行分类,我们需要考虑波可以采取的主要形式。一些乐器,例如钢琴,具有静态衰减,其中它们大多遵循指数衰减形状。另一方面,一些乐器,例如小提琴,可以随着音符的持续而增加或减少音量。除此之外,乐器文件中的一些音频样本会保留到声音结束,而其他音频样本则会提前释放。为了区分衰减是静态的还是动态的,如果衰减因子> 1,或者它偏离衰减曲线太多,则为动态的。为了区分包络是否有释放(AS或ASR),我们查看维持和释放的平均变化率,如果释放的变化率较低,则没有释放。

为了处理音乐文件,我们首先对每个音符频率的信号进行带通滤波。使用滤波后的波,我们迭代每个乐器。对于每种乐器,我们利用乐器的起音(标准化)和释放(标准化)的互相关来找到每个音符的开始和结束,然后利用乐器波和滤波后的音频的 MSE 来获得当时乐器的成本。之后,我们将在傅立叶变换步骤中找到的幅度乘以 1/(我们在此步骤中找到的成本)以获得最终的幅度。
展示 为了显示文件,我们使用 matplotlib 的散点图和 - 形点来显示乐谱。最初,我想根据幅度重新创建音频,但这导致了许多问题,花费了一段时间,并使故障排除变得更加困难。我也尝试使用 matplotlib 的 imshow 图,但在这种情况下效率极低,因为大多数值都是 0,并且每次我们平移或缩放屏幕时,matplotlib 都需要重新绘制每个点,无论它是否在屏幕上。
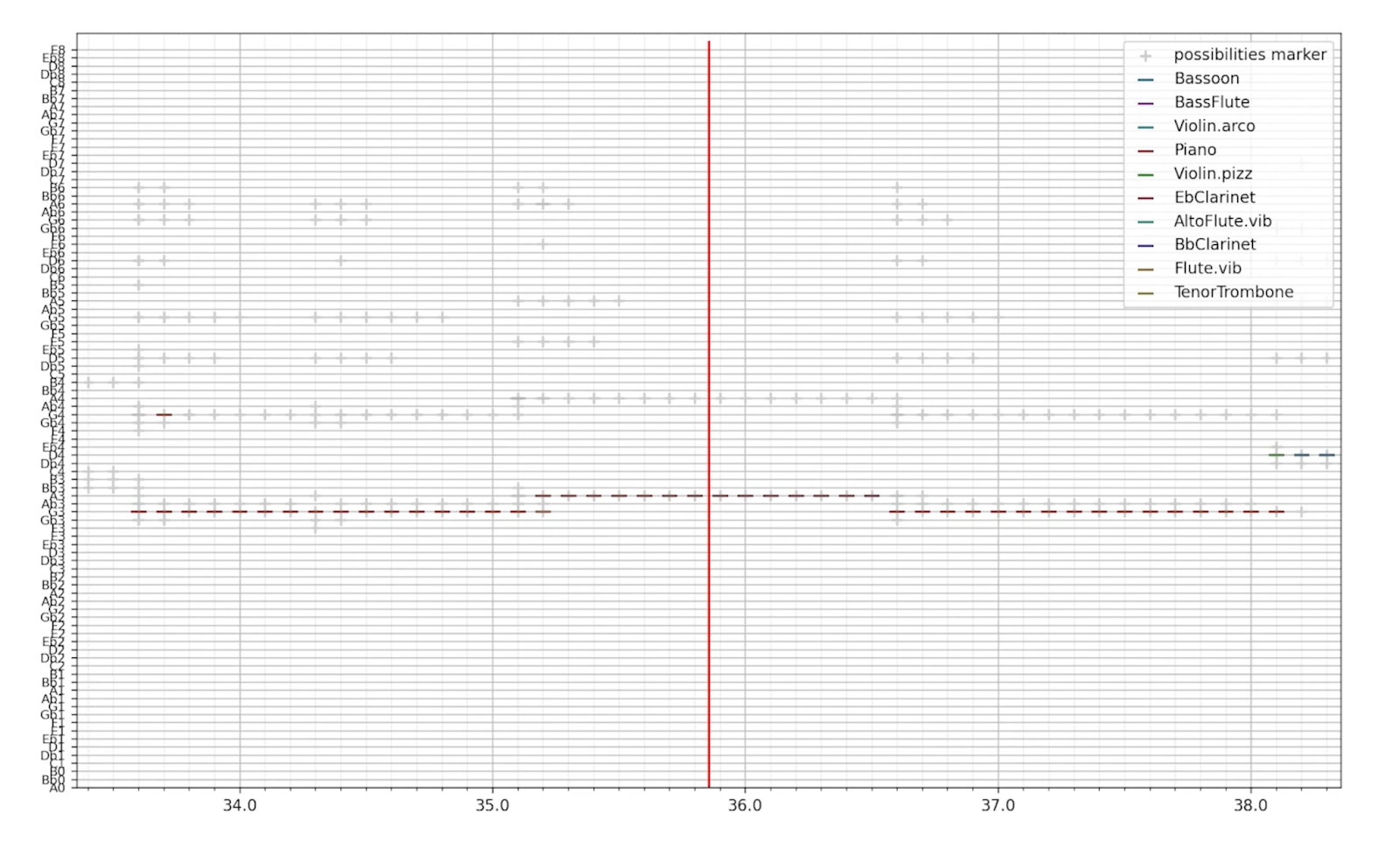
结果
总体效果很好。你可以用它来更好地重现乐谱,特别是当你很难找到正确的音高或和弦时,而且它运行起来也不会花费太多时间。
如何运行项目
-
从GitHub下载后分别运行 ScrapeInstruments.py 和 ProcessInstruments.py 一次 InstrumentAudioFiles 和 InstrumentData 现在应该被填充
-
将 soundfile.read() 可以处理的文件类型上传到 In 文件夹
-
进入 Main.py 并更改任何参数,主要是歌曲的乐器白名单或黑名单。
-
运行 Main.py PlayBack 现在应该为每个输入都有一个文件
-
运行Display.py查看结果!
原文地址:https://blog.csdn.net/xs1997/article/details/143781378
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
