力扣题解2374

大家好，欢迎来到无限大的频道。

今日继续给大家带来力扣题解。

题目描述（中等）：

边积分最高的节点

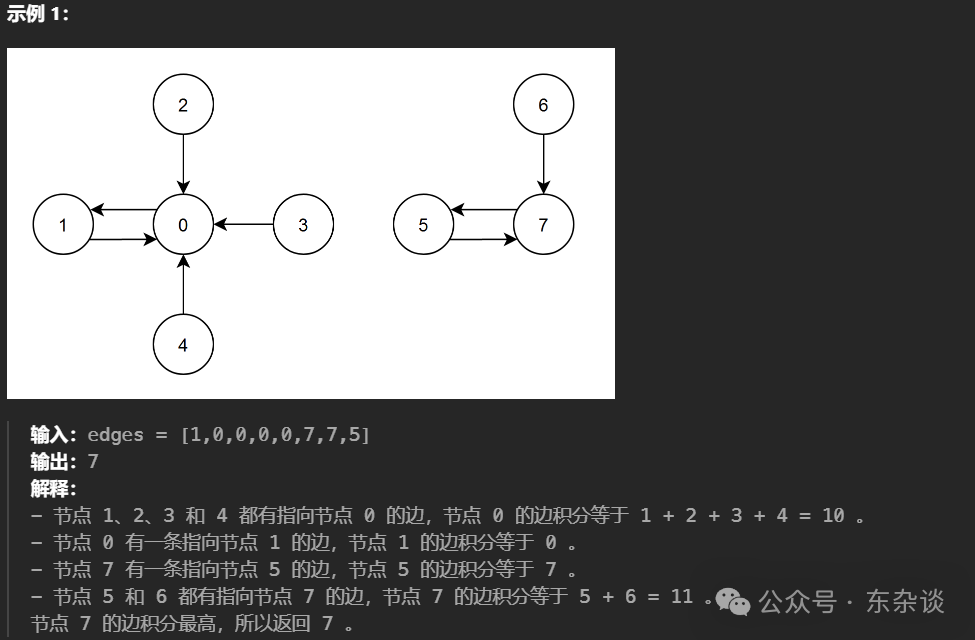
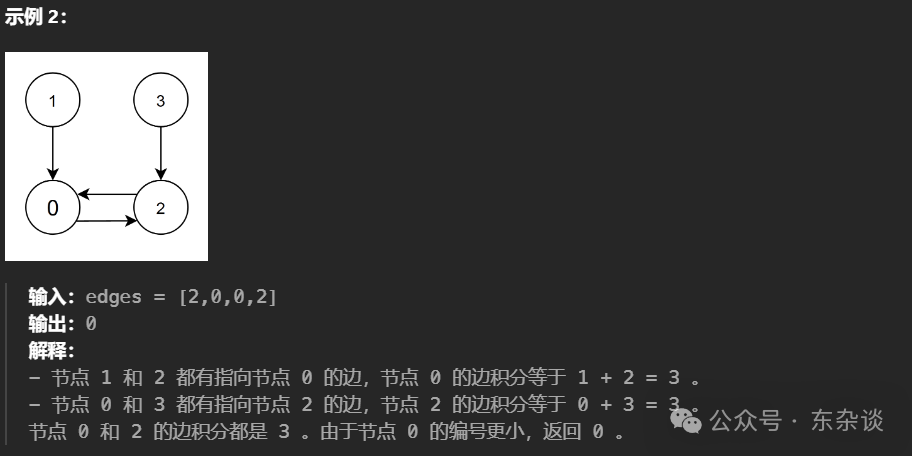
给你一个有向图，图中有 n 个节点，节点编号从 0 到 n - 1 ，其中每个节点都 恰有一条 出边。

图由一个下标从 0 开始、长度为 n 的整数数组 edges 表示，其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的 有向 边。

节点 i 的 边积分 定义为：所有存在一条指向节点 i 的边的节点的 编号 总和。

返回 边积分 最高的节点。如果多个节点的 边积分 相同，返回编号 最小 的那个。

解题思路：

我们需要计算每个节点的边积分，即所有指向该节点的边的源节点编号的总和。由于每个节点只有一条出边，我们可以利用一个数组来存储每个节点的边积分。

步骤：

1. 初始化一个长度为 n 的数组 in_degree_sum，用于存储每个节点的边积分。

2. 遍历 edges 数组，对于每个节点 i，更新指向 edges[i] 的节点的边积分。例如，将 i 加到 in_degree_sum[edges[i]] 中。

3. 找到 in_degree_sum 中的最大值及其对应的节点。如果有多个节点有相同的边积分，返回编号最小的节点。

参考代码：

int edgeScore(int* edges, int edgesSize) {
    long long in_degree_sum[edgesSize];
    for(int i = 0; i < edgesSize; i++){
        in_degree_sum[i] = 0;
    }

     for (int i = 0; i < edgesSize; i++) {
        in_degree_sum[edges[i]] += i;  // 将节点 i 加到 edges[i] 的积分中
    }

    int max_node = 0;
    long long max_sum = in_degree_sum[0];

    for(int i = 0; i < edgesSize; i++){
        if(in_degree_sum[i] > max_sum){
            max_sum = in_degree_sum[i];
            max_node = i;
        }
    }

    return max_node;
}

函数逻辑概述

-输入: 一个整数数组 `edges`，表示有向图中每个节点的出边。

-目标: 计算每个节点的边积分，最终返回边积分最高的节点编号。如果有多个节点的边积分相同，返回编号最小的那个。

时间复杂度分析

函数的主要操作可以分为三个部分：

1. 初始化 `in_degree_sum` 数组:

   for(int i = 0; i < edgesSize; i++){
       in_degree_sum[i] = 0;
   }

   这个循环的时间复杂度是 O(n)，其中 n 是 `edgesSize`。

2. 计算边积分:

    for (int i = 0; i < edgesSize; i++) {
       in_degree_sum[edges[i]] += i;  // 将节点 i 加到 edges[i] 的积分中
   }

   这个循环的时间复杂度也是 O(n)。

3. 查找边积分最高的节点:

 for(int i = 0; i < edgesSize; i++){
       if(in_degree_sum[i] > max_sum){
           max_sum = in_degree_sum[i];
           max_node = i;
       }
   }

   这个循环的时间复杂度同样是 O(n)。

将这三部分的时间复杂度相加，我们得到：

- 总时间复杂度: O(n) + O(n) + O(n) = O(n)

空间复杂度分析

函数使用了一个额外的数组 `in_degree_sum` 来存储每个节点的边积分，其大小为 `edgesSize`。因此，空间复杂度分析如下：

- 额外空间: `in_degree_sum` 数组的大小为 n，因此空间复杂度为 O(n)。

除了 `in_degree_sum` 数组外，函数中使用的其他变量（如 `max_node`, `max_sum` 和循环变量）只占用常数空间，不会随输入规模变化。

总结

- 时间复杂度: O(n)

- 空间复杂度: O(n)

原文地址：https://blog.csdn.net/wxdzuishaui/article/details/142418460

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！