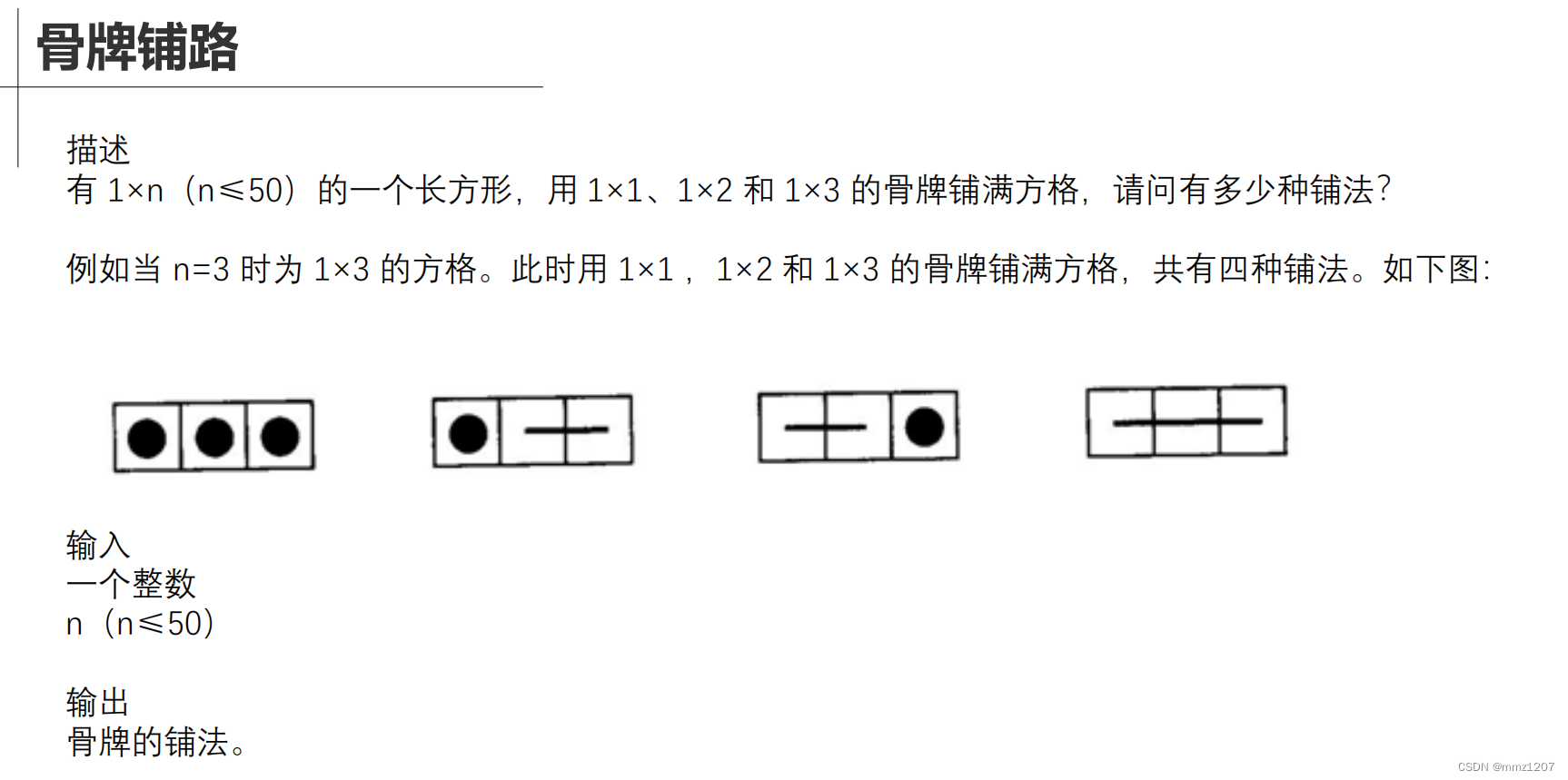
函数——递归(c++)
递归是一种类似枚举的方法，可以理解为“函数的自我调用”。
递归比循环枚举解决的问题多，所以递归包含了循环枚举。
#include <iostream>
using namespace std;
int aaa(int);
int q;
int main()
{
cin>>q;
cout<<aaa(q);
return 0;
}
int aaa(int a)
{
if(a==1) return 1;
if(a==2) return 2;
if(a==3) return 4;
int b = aaa(a-1)+aaa(a-2)+aaa(a-3);
return b;
}
#include <iostream>
using namespace std;
int aaa(int);
int q;
int main()
{
cin>>q;
cout<<aaa(q);
return 0;
}
int aaa(int a)
{
if(a==1) return 1;
if(a==2) return 1;
int b = aaa(a-1)+aaa(a-2);
return b;
}
数列求和
题目描述
有一数列如下： 1 2 4 7 11 16 22 …… 试求该数列前
N
项之和。
输入
一个整数
N
（ 0<
N
<1000 ）。
输出
一个整数。
输入复制
6
输出复制
41
青少年编程
#include <iostream>
using namespace std;
int aaa(int);
int q;
int sum = 0;
int main()
{
cin>>q;
int w = aaa(q);
sum = sum+1;
cout<<sum;
return 0;
}
int aaa(int a)
{
if(a==1) return 1;
int b = aaa(a-1)+a-1;
sum = sum+b;
return b;
}
PELL数列
描述
Pell数列a1, a2, a3, ...的定义是这样的，a(1) = 1, a(2) = 2, ... , a(n) = 2 * a(n
−
1 )+ a(n - 2) (n > 2)。
给出一个正整数k，要求Pell数列的第k项模上32767是多少。
输入
第1行是测试数据的组数n，后面跟着n行输入。每组测试数据占1行，包括一个正整数k (1 ≤ k <
1000000)。
输出
n行，每行输出对应一个输入。输出应是一个非负整数。
样例输入
2
1
8
样例输出
1
408
#include <iostream>
using namespace std;
int aaa(int);
int q;
int a[25] = {0};
int main()
{
cin>>q;
for(int i = 0;i<q;i++)
{
cin>>a[i];
}
cout<<endl;
for(int i = 0;i<q;i++)
{
cout<<aaa(a[i])<<endl;
}
return 0;
}
int aaa(int a)
{
if(a==1) return 1;
if(a==2) return 2;
int b = 2*aaaa(a-1)+aaa(a-2);
return b;
}
斐波那契数列
描述
菲波那契数列是指这样的数列: 数列的第一个和第二个数都为1，接
下来每个数都等于前面2个数之和。
给出一个正整数a，要求菲波那契数列中第a个数是多少。
输入
第1行是测试数据的组数n，后面跟着n行输入。每组测试数据占1行，
包括一个正整数a(1 <= a <= 20)
输出
输出有n行，每行输出对应一个输入。输出应是一个正整数，为菲
波那契数列中第a个数的大小
样例输入
4
5
2
19
1
样例输出
5
1
4181
1
#include <iostream>
using namespace std;
int aaa(int);
int q;
int a[25] = {0};
int main()
{
cin>>q;
for(int i = 0;i<q;i++)
{
cin>>a[i];
}
cout<<endl;
for(int i = 0;i<q;i++)
{
cout<<aaa(a[i])<<endl;
}
return 0;
}
int aaa(int a)
{
if(a==1) return 1;
if(a==2) return 1;
int b = aaa(a-1)+aaa(a-2);
return b;
}原文地址：https://blog.csdn.net/mmz1207/article/details/136142644
免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！