C1-3.2 关于‘神经网络’

C1-3.2 关于‘神经网络’

【注释】

彩色图像（RGB）由三原色构成，二维图像在任意一个点像素为立体三层结构，分别是红色、绿色、蓝色值，该值的范围在0∽255之间

1、全连接神经网络——整体架构

【注释】：

​ 这张图懂了的话，神经网络就懂了80%。

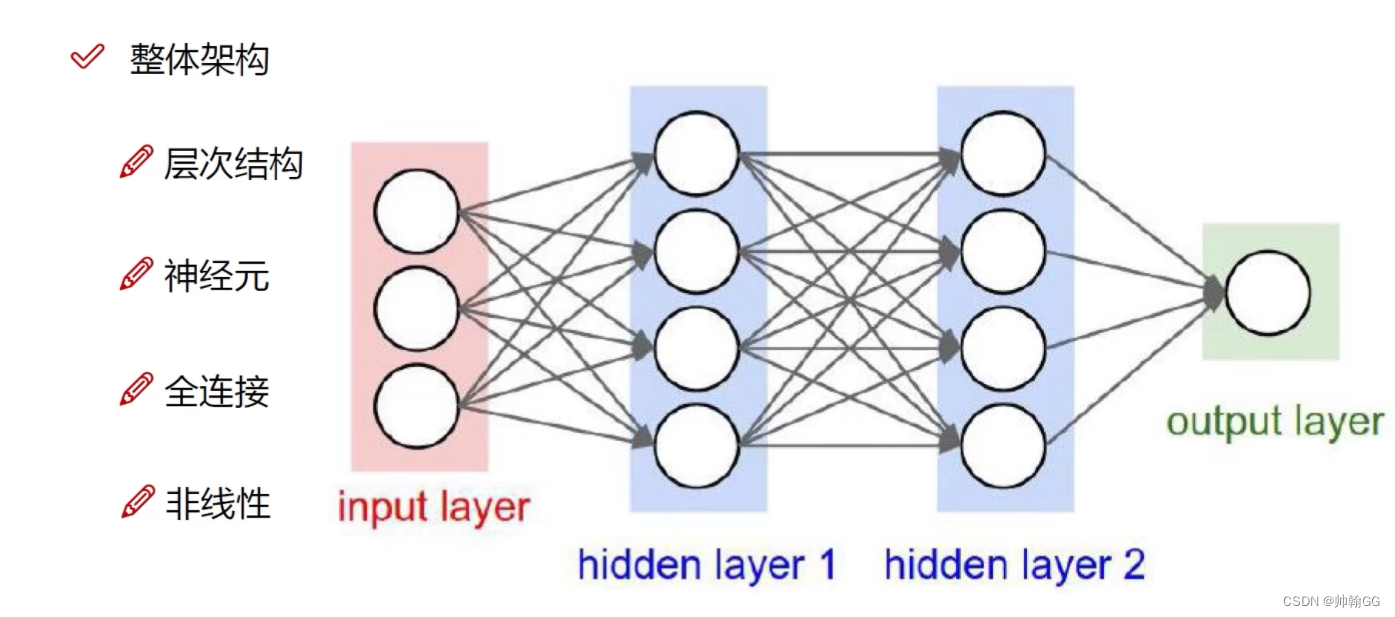
1、层次结构

分为：

• 输入层
• 隐藏层
• 输出层

ps：要注意的是，中间的隐藏层可以由多层组成。

展示一下过程吧;

​ 输入层输入数据 (输入层数据* W1)> hidden layer1 (hidden layer1层数据 * W2)>hidden layer2 (hidden layer2 层数据 * W3 )>输出层

PS：W1 W2 W3 可以是一个数，也可以是n * m的矩阵

1.1 、层次结构—神经元 （输入层）

就是 输入层（input layer）小红框中那几个小汤圆（A、B、C），代表三个输入的特征的个数

​ 这三个大汤圆：A,B,C 分别代表三个特征值（比如：身高、体重、年龄）

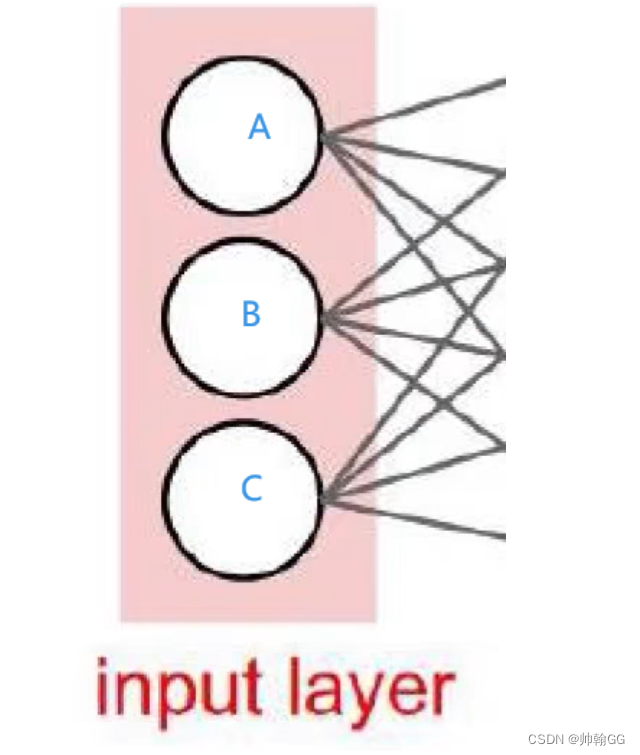
​ 我们可以看到图中每个层次中都有许多圆圆的球似的东西，这个东西就是在神经网络中的神经元，每一种层次中的神经元中的含量不太一样。

​ 在输入层中的每一个神经元里面是你输入原始数据（一般称为X）的不同特征，比如x为一张图片，这张图片的像素是32 * 32 * 3 = 3072，其中的每一个像素都是它的特征，所以有3072个特征对应的输入层神经元个数就是3072个，这些特征以矩阵的形式进行输入的。我们举个例子比如我们的输入矩阵为‘1*3072’（第一维的数字表示一个batch（batch指的是每次训练输入多少个数据）中有多少个输入；第二维数字中的就是每一个输入有多少特征。）

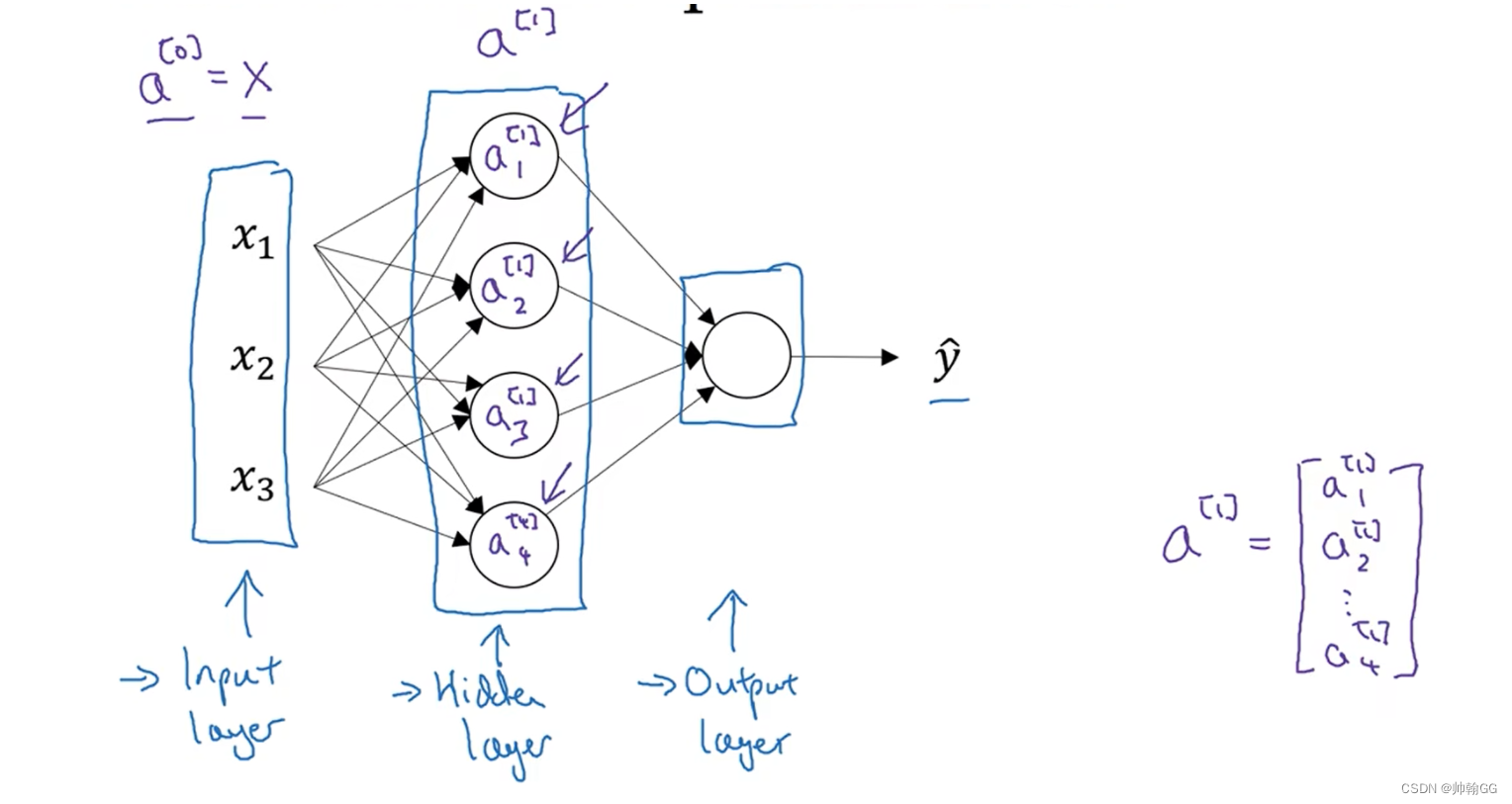
1.2、层次结构—隐藏层

• **隐藏层的含义来源：**不像输入层（在监督学习的训练集中，我们知道输入的数据X-> ；w -> ；b）、输出层（在监督学习的训练集中，知道输出结果）。隐藏层：在训练集中我们是看不到他的值的。

• 在 “隐藏层” 和 “输出层”中，可以把每一个神经元当做一个激活函数，激活函数可以是Sigmoid ；RueL等等…

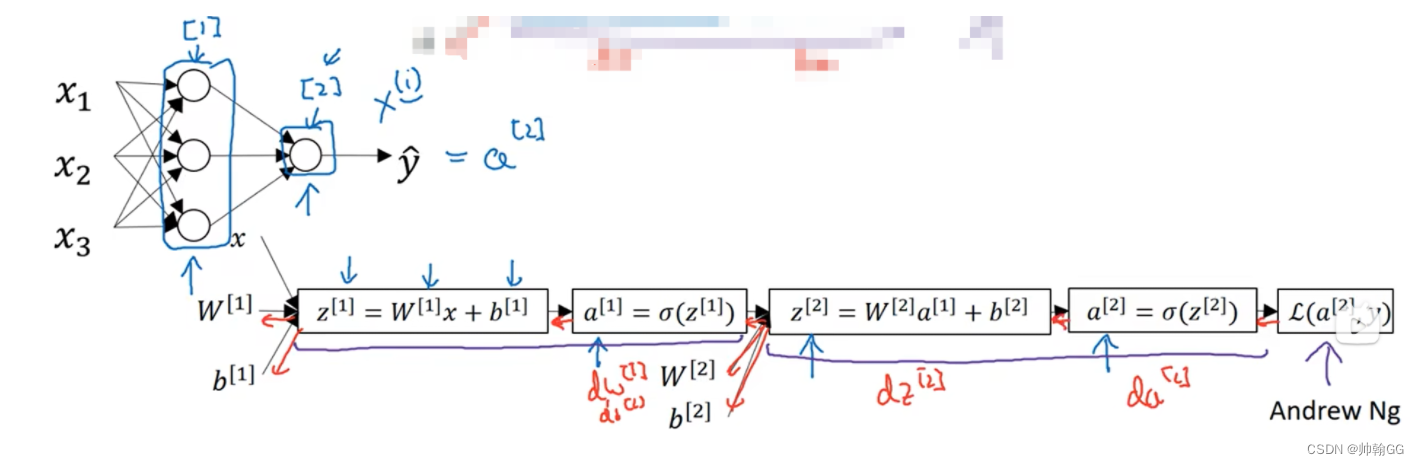
• 以 一个神经元结构为例：

  • 其中L是最后一步计算损失函数，然后进行梯度下降进行后反馈，不断优化w 和b 的值，得到最小的损失函数值。

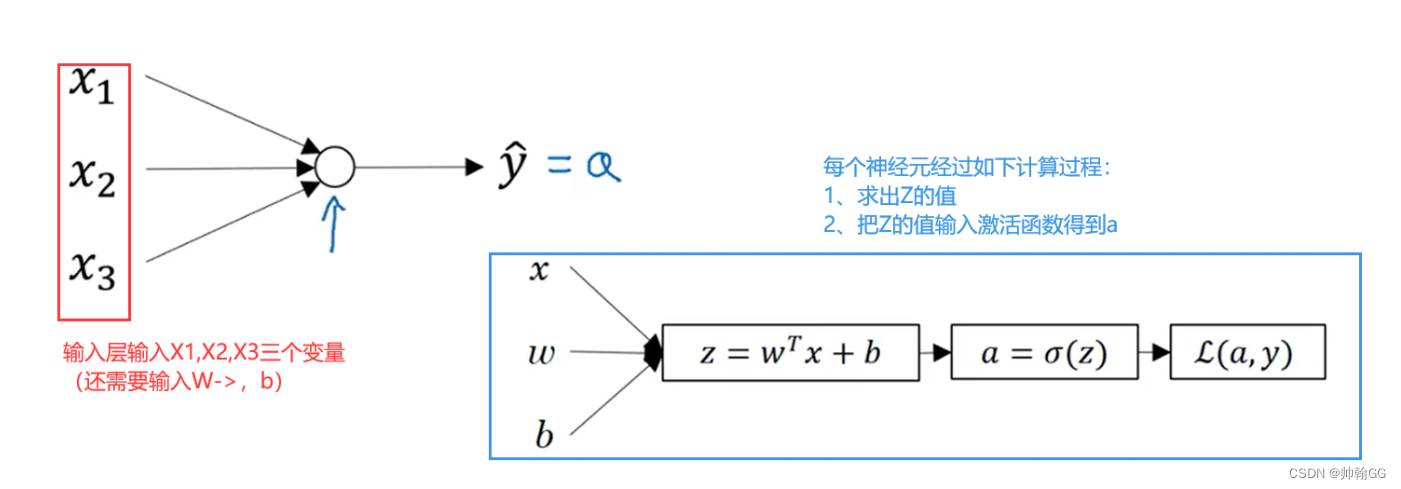
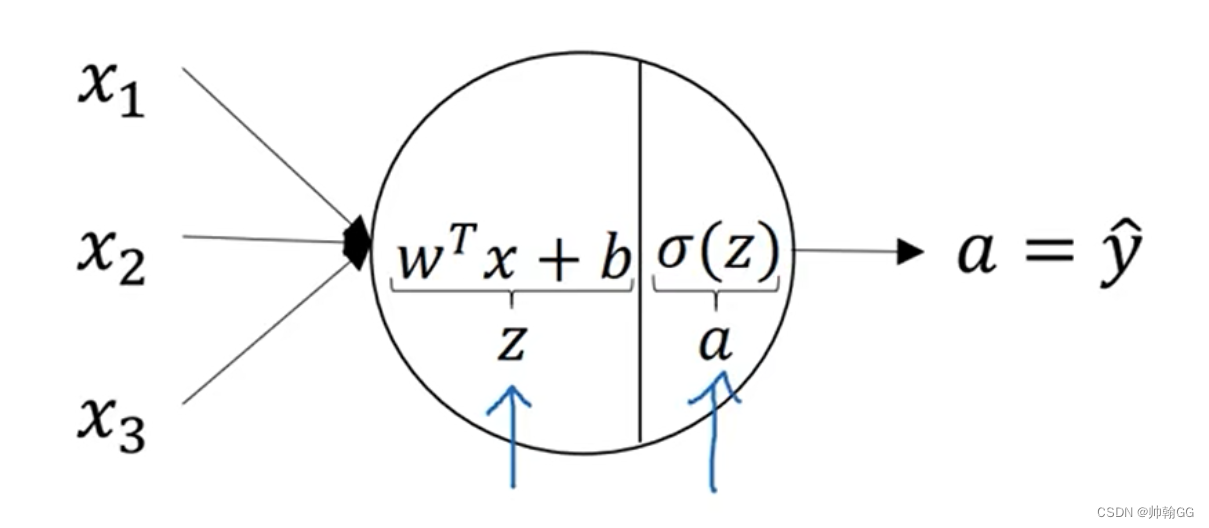
• 多层隐藏层的情况：

  【注释】：其中a[0]表示输入层输入的值（可以是向量）

  • 第一层隐藏层相应参数和结果：a[1] ；w[1]； b[1]
    • 第一层神经元各个结果：a[1]1,a[1]2,a[1]3
  • 第二层隐藏层相应参数和结果：a[2] w[2] b[2]

  用这种可以明确表示出这些值来自那一层。。。

1.3、层次结构—输出层

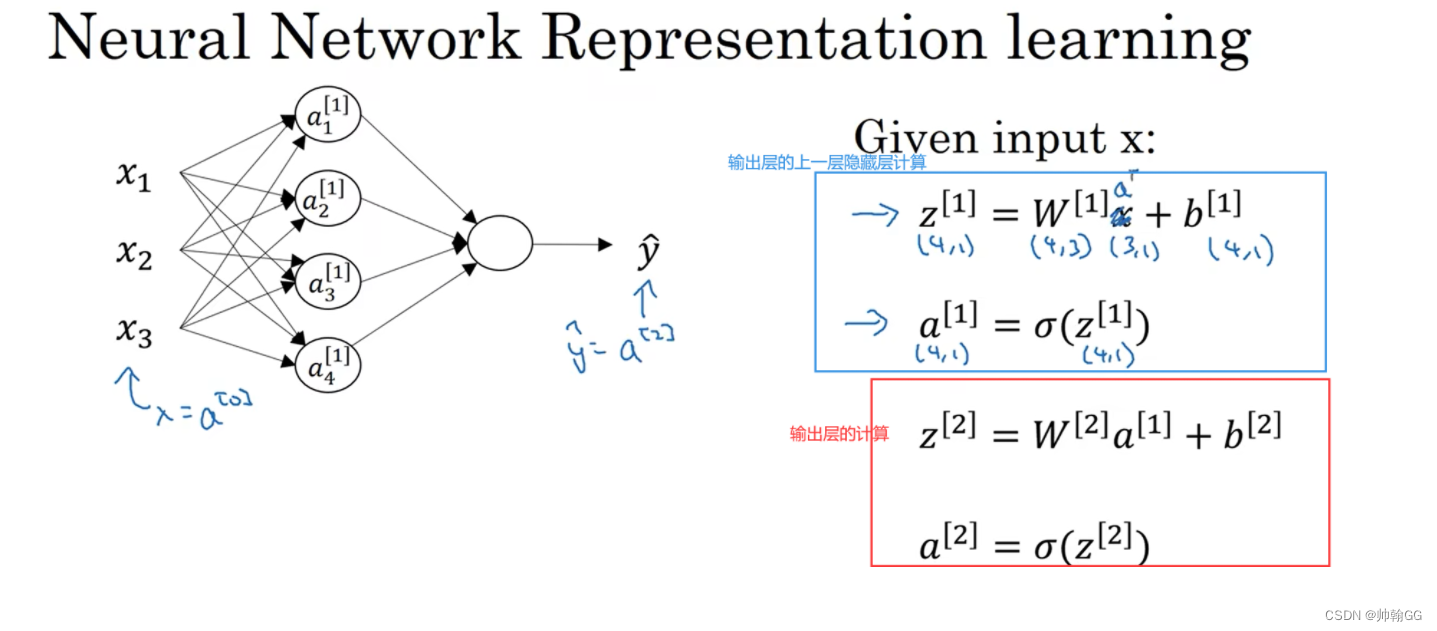
输出层 可以是一个神经元/多个神经元

​

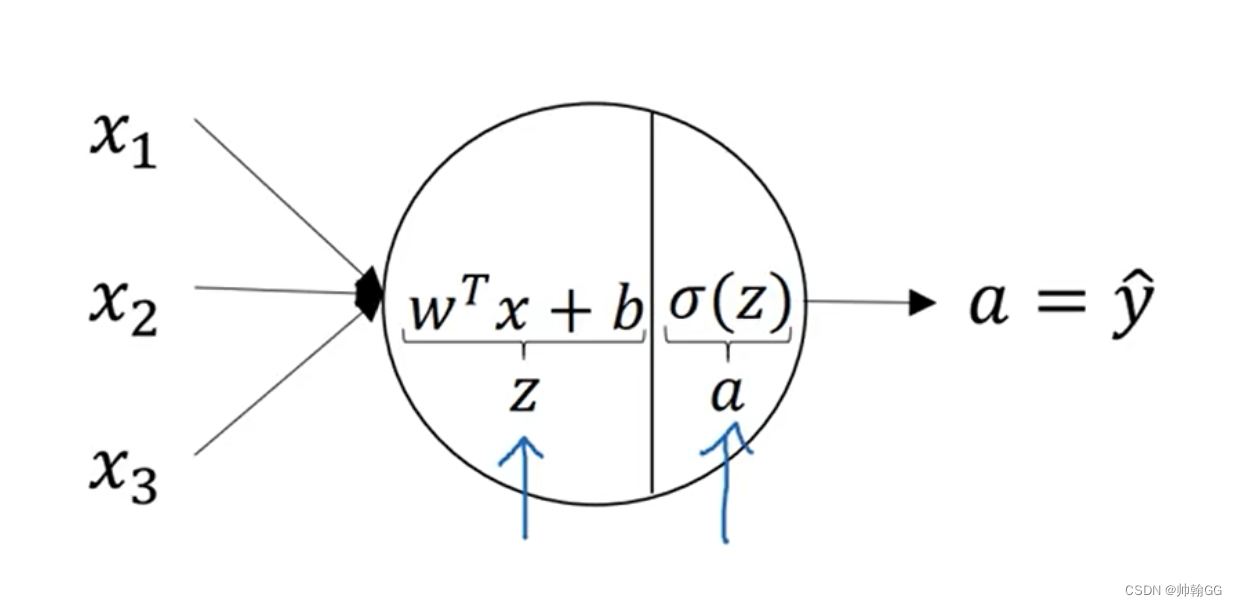
以一个神经元为例：

• 第一步：接受前一层隐藏层的输出（这里是a[1]），作为输出层的输入
• 第二步：放入输出层的神经元进行计算。

原文地址：https://blog.csdn.net/weixin_46228946/article/details/135566259

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！