基于关联分析与聚类的空气质量研究

🕗 发布于 2024-11-18 11:38 聚类数据挖掘 k-means

1.项目背景

本项目基于 UCI 空气质量数据集，该数据集包含 9358 条逐小时的空气质量监测记录，覆盖了 2004 年 3 月至 2005 年 2 月的时间跨度。数据采集地点位于意大利一处交通密集、污染较为严重的地区，监测设备位于地面附近。本项目深入分析了该地区在不同时段和气象条件下的空气污染特征，探索了不同污染物之间的关联关系及其与环境条件的相互影响，这不仅有助于更好地理解空气污染的动态变化，还可以为优化空气质量监测网络、制定有效的污染控制政策提供数据支持。

2.数据说明

字段	说明
Date	测量的日期。
Time	测量的时间。
CO(GT)	空气中一氧化碳（CO）的浓度（微克/立方米）。
PT08.S1(CO)	用于测量一氧化碳（CO）浓度的传感器读数。
NMHC(GT)	非甲烷烃类（NMHC）的浓度（微克/立方米）。
C6H6(GT)	空气中苯（C6H6）的浓度（微克/立方米）。
PT08.S2(NMHC)	用于测量非甲烷烃类（NMHC）浓度的传感器读数。
NOx(GT)	空气中氮氧化物（NOx）的浓度（微克/立方米）。
PT08.S3(NOx)	用于测量氮氧化物（NOx）浓度的传感器读数。
NO2(GT)	空气中二氧化氮（NO2）的浓度（微克/立方米）。
PT08.S4(NO2)	用于测量二氧化氮（NO2）浓度的传感器读数。
PT08.S5(O3)	用于测量臭氧（O3）浓度的传感器读数。
T	温度（Temperature），表示空气的温度，单位可能为摄氏度 (°C)。
RH	相对湿度（Relative Humidity），百分比值，表示空气中水蒸气含量与该温度下最大含量的比例。
AH	绝对湿度（Absolute Humidity），表示空气中水蒸气的实际含量，单位为克/立方米 (g/m³)。

3.Python库导入及数据读取

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.decomposition import PCA
from mlxtend.frequent_patterns import apriori, association_rules

data = pd.read_csv("/home/mw/input/11086850/AirQualityUCI.csv")

4.数据预览及预处理

print('查看数据信息:')
data.info()

查看数据信息:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 9471 entries, 0 to 9470
Data columns (total 15 columns):
 #   Column         Non-Null Count  Dtype  
---  ------         --------------  -----  
 0   Date           9357 non-null   object 
 1   Time           9357 non-null   object 
 2   CO(GT)         9357 non-null   float64
 3   PT08.S1(CO)    9357 non-null   float64
 4   NMHC(GT)       9357 non-null   float64
 5   C6H6(GT)       9357 non-null   float64
 6   PT08.S2(NMHC)  9357 non-null   float64
 7   NOx(GT)        9357 non-null   float64
 8   PT08.S3(NOx)   9357 non-null   float64
 9   NO2(GT)        9357 non-null   float64
 10  PT08.S4(NO2)   9357 non-null   float64
 11  PT08.S5(O3)    9357 non-null   float64
 12  T              9357 non-null   float64
 13  RH             9357 non-null   float64
 14  AH             9357 non-null   float64
dtypes: float64(13), object(2)
memory usage: 1.1+ MB

print(f'查看重复值:{data.duplicated().sum()}')

查看重复值:113

data[data.duplicated()].head()

	Date	Time	CO(GT)	PT08.S1(CO)	NMHC(GT)	C6H6(GT)	PT08.S2(NMHC)	NOx(GT)	PT08.S3(NOx)	NO2(GT)	PT08.S4(NO2)	PT08.S5(O3)	T	RH	AH
9358	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
9359	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
9360	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
9361	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
9362	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

在检查重复值时，发现数据中有一部分行完全是缺失值（即所有特征列都为 NaN）。这些行被标记为重复行。

# 删除完全为空值的重复行
data = data.dropna(how='all')  # 删除所有列都是NaN的行

print('检查删除全空重复值后的数据集中是否仍有缺失值:')
data.isnull().sum()

检查删除全空重复值后的数据集中是否仍有缺失值:





Date             0
Time             0
CO(GT)           0
PT08.S1(CO)      0
NMHC(GT)         0
C6H6(GT)         0
PT08.S2(NMHC)    0
NOx(GT)          0
PT08.S3(NOx)     0
NO2(GT)          0
PT08.S4(NO2)     0
PT08.S5(O3)      0
T                0
RH               0
AH               0
dtype: int64

在删除了完全空的重复行后，数据集中已不再存在缺失值，这表明所有的缺失值都集中在这些全为空值的重复行中，然后将 Date 和 Time 列合并并转换为 datetime 格式，以便后续分析。

# 将 Date 和 Time 列合并并转换为 datetime 格式，以便后续分析
data['Datetime'] = pd.to_datetime(data['Date'] + ' ' + data['Time'], errors='coerce')

# 删除原来的 Date 和 Time 列，保留转换后的 Datetime 列
data = data.drop(columns=['Date', 'Time'])

feature_map = {
    'CO(GT)': '一氧化碳浓度',
    'PT08.S1(CO)': 'CO传感器读数',
    'NMHC(GT)': '非甲烷烃浓度',
    'C6H6(GT)': '苯浓度',
    'PT08.S2(NMHC)': '非甲烷烃传感器读数',
    'NOx(GT)': '氮氧化物浓度',
    'PT08.S3(NOx)': '氮氧化物传感器读数',
    'NO2(GT)': '二氧化氮浓度',
    'PT08.S4(NO2)': '二氧化氮传感器读数',
    'PT08.S5(O3)': '臭氧传感器读数',
    'T': '温度',
    'RH': '相对湿度',
    'AH': '绝对湿度'
}

plt.figure(figsize=(20, 20))
for i, (col, col_name) in enumerate(feature_map.items(), 1):
    plt.subplot(4, 4, i)
    sns.boxplot(y=data[col])
    plt.title(f'{col_name}的箱线图', fontsize=14)
    plt.ylabel('数值', fontsize=12)
    plt.grid(axis='y', linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

数据中每个数值型特征都存在 -200的异常值，这里考虑其为未观测到的数据，数据为时序数据，可以考虑插值法和一些中位数、均值填充的方法。

# 统计每列中值为 -200 的数量，以便了解异常值的分布情况
print("显示每列中值为 -200 的数量：")
(data == -200).sum()

显示每列中值为 -200 的数量：





CO(GT)           1683
PT08.S1(CO)       366
NMHC(GT)         8443
C6H6(GT)          366
PT08.S2(NMHC)     366
NOx(GT)          1639
PT08.S3(NOx)      366
NO2(GT)          1642
PT08.S4(NO2)      366
PT08.S5(O3)       366
T                 366
RH                366
AH                366
Datetime            0
dtype: int64

对于大量缺失的 NMHC(GT) 列，考虑删除，因其数据质量较差，填补的话，但可靠性可能会受影响。
对于其他列，可以使用插值法填充。

# 删除缺失值过多的列（NMHC(GT)）
data = data.drop(columns=['NMHC(GT)'])

# 将 `-200` 替换为 `NaN` 以表示缺失值
data.replace(-200, np.nan, inplace=True)

# 保存填充前的统计信息（替换为 NaN 后的整列统计信息）
missing_stats_before = {}
for col in data.columns:
    if col != 'Datetime' and not col.endswith('_Missing_Flag'):
        # 整列的描述性统计信息
        missing_stats_before[col] = data[col].describe()

# 为每一列创建标记缺失值位置的列，用于对比插值后数据
for col in data.columns:
    if col != 'Datetime':
        data[f'{col}_Missing_Flag'] = data[col].isna().astype(int)

# 将 `Datetime` 列设为索引并按时间排序
data.set_index('Datetime', inplace=True)
data.sort_index(inplace=True)

# 使用时间序列插值方法填充缺失值
data.interpolate(method='time', inplace=True)

# 将索引 `Datetime` 转回普通列，并放在数据框的第一列
data.reset_index(inplace=True)

# 确保 `Datetime` 列在第一列位置
columns_order = ['Datetime'] + [col for col in data.columns if col != 'Datetime']
data = data[columns_order]

# 保存填充后的统计信息（整列统计信息）
missing_stats_after = {}
for col in missing_stats_before.keys():
    missing_stats_after[col] = data[col].describe()

# 输出对比结果
for col in missing_stats_before.keys():
    print(f"\n=== 列 '{col}' 填充前后的统计信息对比 ===")
    print("填充前整列统计信息:")
    print(missing_stats_before[col])
    print("填充后整列统计信息:")
    print(missing_stats_after[col])

=== 列 'CO(GT)' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    7674.000000
mean        2.152750
std         1.453252
min         0.100000
25%         1.100000
50%         1.800000
75%         2.900000
max        11.900000
Name: CO(GT), dtype: float64
填充后整列统计信息:
count    9357.000000
mean        2.130603
std         1.431736
min         0.100000
25%         1.100000
50%         1.800000
75%         2.900000
max        11.900000
Name: CO(GT), dtype: float64

=== 列 'PT08.S1(CO)' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    8991.000000
mean     1099.833166
std       217.080037
min       647.000000
25%       937.000000
50%      1063.000000
75%      1231.000000
max      2040.000000
Name: PT08.S1(CO), dtype: float64
填充后整列统计信息:
count    9357.000000
mean     1103.059741
std       218.196346
min       647.000000
25%       938.000000
50%      1067.000000
75%      1239.000000
max      2040.000000
Name: PT08.S1(CO), dtype: float64

=== 列 'C6H6(GT)' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    8991.000000
mean       10.083105
std         7.449820
min         0.100000
25%         4.400000
50%         8.200000
75%        14.000000
max        63.700000
Name: C6H6(GT), dtype: float64
填充后整列统计信息:
count    9357.000000
mean       10.179155
std         7.503812
min         0.100000
25%         4.500000
50%         8.300000
75%        14.100000
max        63.700000
Name: C6H6(GT), dtype: float64

=== 列 'PT08.S2(NMHC)' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    8991.000000
mean      939.153376
std       266.831429
min       383.000000
25%       734.500000
50%       909.000000
75%      1116.000000
max      2214.000000
Name: PT08.S2(NMHC), dtype: float64
填充后整列统计信息:
count    9357.000000
mean      942.142620
std       267.866611
min       383.000000
25%       736.000000
50%       910.012987
75%      1119.000000
max      2214.000000
Name: PT08.S2(NMHC), dtype: float64

=== 列 'NOx(GT)' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    7718.000000
mean      246.896735
std       212.979168
min         2.000000
25%        98.000000
50%       180.000000
75%       326.000000
max      1479.000000
Name: NOx(GT), dtype: float64
填充后整列统计信息:
count    9357.000000
mean      241.922197
std       204.315075
min         2.000000
25%        96.000000
50%       180.000000
75%       326.000000
max      1479.000000
Name: NOx(GT), dtype: float64

=== 列 'PT08.S3(NOx)' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    8991.000000
mean      835.493605
std       256.817320
min       322.000000
25%       658.000000
50%       806.000000
75%       969.500000
max      2683.000000
Name: PT08.S3(NOx), dtype: float64
填充后整列统计信息:
count    9357.000000
mean      832.758897
std       255.709833
min       322.000000
25%       654.000000
50%       804.000000
75%       968.000000
max      2683.000000
Name: PT08.S3(NOx), dtype: float64

=== 列 'NO2(GT)' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    7715.000000
mean      113.091251
std        48.370108
min         2.000000
25%        78.000000
50%       109.000000
75%       142.000000
max       340.000000
Name: NO2(GT), dtype: float64
填充后整列统计信息:
count    9357.000000
mean      109.632094
std        46.462311
min         2.000000
25%        76.000000
50%       104.917526
75%       136.314685
max       340.000000
Name: NO2(GT), dtype: float64

=== 列 'PT08.S4(NO2)' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    8991.000000
mean     1456.264598
std       346.206794
min       551.000000
25%      1227.000000
50%      1463.000000
75%      1674.000000
max      2775.000000
Name: PT08.S4(NO2), dtype: float64
填充后整列统计信息:
count    9357.000000
mean     1453.298814
std       343.206131
min       551.000000
25%      1227.000000
50%      1460.000000
75%      1668.000000
max      2775.000000
Name: PT08.S4(NO2), dtype: float64

=== 列 'PT08.S5(O3)' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    8991.000000
mean     1022.906128
std       398.484288
min       221.000000
25%       731.500000
50%       963.000000
75%      1273.500000
max      2523.000000
Name: PT08.S5(O3), dtype: float64
填充后整列统计信息:
count    9357.000000
mean     1032.544298
std       404.447613
min       221.000000
25%       733.000000
50%       970.000000
75%      1293.000000
max      2523.000000
Name: PT08.S5(O3), dtype: float64

=== 列 'T' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    8991.000000
mean       18.317829
std         8.832116
min        -1.900000
25%        11.800000
50%        17.800000
75%        24.400000
max        44.600000
Name: T, dtype: float64
填充后整列统计信息:
count    9357.000000
mean       18.233408
std         8.781791
min        -1.900000
25%        11.700000
50%        17.600000
75%        24.300000
max        44.600000
Name: T, dtype: float64

=== 列 'RH' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    8991.000000
mean       49.234201
std        17.316892
min         9.200000
25%        35.800000
50%        49.600000
75%        62.500000
max        88.700000
Name: RH, dtype: float64
填充后整列统计信息:
count    9357.000000
mean       49.191386
std        17.194506
min         9.200000
25%        35.800000
50%        49.600000
75%        62.300000
max        88.700000
Name: RH, dtype: float64

=== 列 'AH' 填充前后的统计信息对比 ===
填充前整列统计信息:
count    8991.000000
mean        1.025530
std         0.403813
min         0.184700
25%         0.736800
50%         0.995400
75%         1.313700
max         2.231000
Name: AH, dtype: float64
填充后整列统计信息:
count    9357.000000
mean        1.019621
std         0.402203
min         0.184700
25%         0.732300
50%         0.989500
75%         1.306700
max         2.231000
Name: AH, dtype: float64

通过对比填充前后各列的描述性情况，发现统计特征变化很小，而且极值也没发生变化，可以认为填充效果较好。

data = data.iloc[:, :13]

data.head()

	Datetime	CO(GT)	PT08.S1(CO)	C6H6(GT)	PT08.S2(NMHC)	NOx(GT)	PT08.S3(NOx)	NO2(GT)	PT08.S4(NO2)	PT08.S5(O3)	T	RH	AH
0	2004-03-10 18:00:00	2.6	1360.0	11.9	1046.0	166.0	1056.0	113.0	1692.0	1268.0	13.6	48.9	0.7578
1	2004-03-10 19:00:00	2.0	1292.0	9.4	955.0	103.0	1174.0	92.0	1559.0	972.0	13.3	47.7	0.7255
2	2004-03-10 20:00:00	2.2	1402.0	9.0	939.0	131.0	1140.0	114.0	1555.0	1074.0	11.9	54.0	0.7502
3	2004-03-10 21:00:00	2.2	1376.0	9.2	948.0	172.0	1092.0	122.0	1584.0	1203.0	11.0	60.0	0.7867
4	2004-03-10 22:00:00	1.6	1272.0	6.5	836.0	131.0	1205.0	116.0	1490.0	1110.0	11.2	59.6	0.7888

feature_map = {
    'CO(GT)': '一氧化碳浓度',
    'PT08.S1(CO)': 'CO传感器读数',
    'C6H6(GT)': '苯浓度',
    'PT08.S2(NMHC)': '非甲烷烃传感器读数',
    'NOx(GT)': '氮氧化物浓度',
    'PT08.S3(NOx)': '氮氧化物传感器读数',
    'NO2(GT)': '二氧化氮浓度',
    'PT08.S4(NO2)': '二氧化氮传感器读数',
    'PT08.S5(O3)': '臭氧传感器读数',
    'T': '温度',
    'RH': '相对湿度',
    'AH': '绝对湿度'
}

plt.figure(figsize=(20, 15))
for i, (col, col_name) in enumerate(feature_map.items(), 1):
    plt.subplot(3, 4, i)
    sns.boxplot(y=data[col])
    plt.title(f'{col_name}的箱线图', fontsize=14)
    plt.ylabel('数值', fontsize=12)
    plt.grid(axis='y', linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

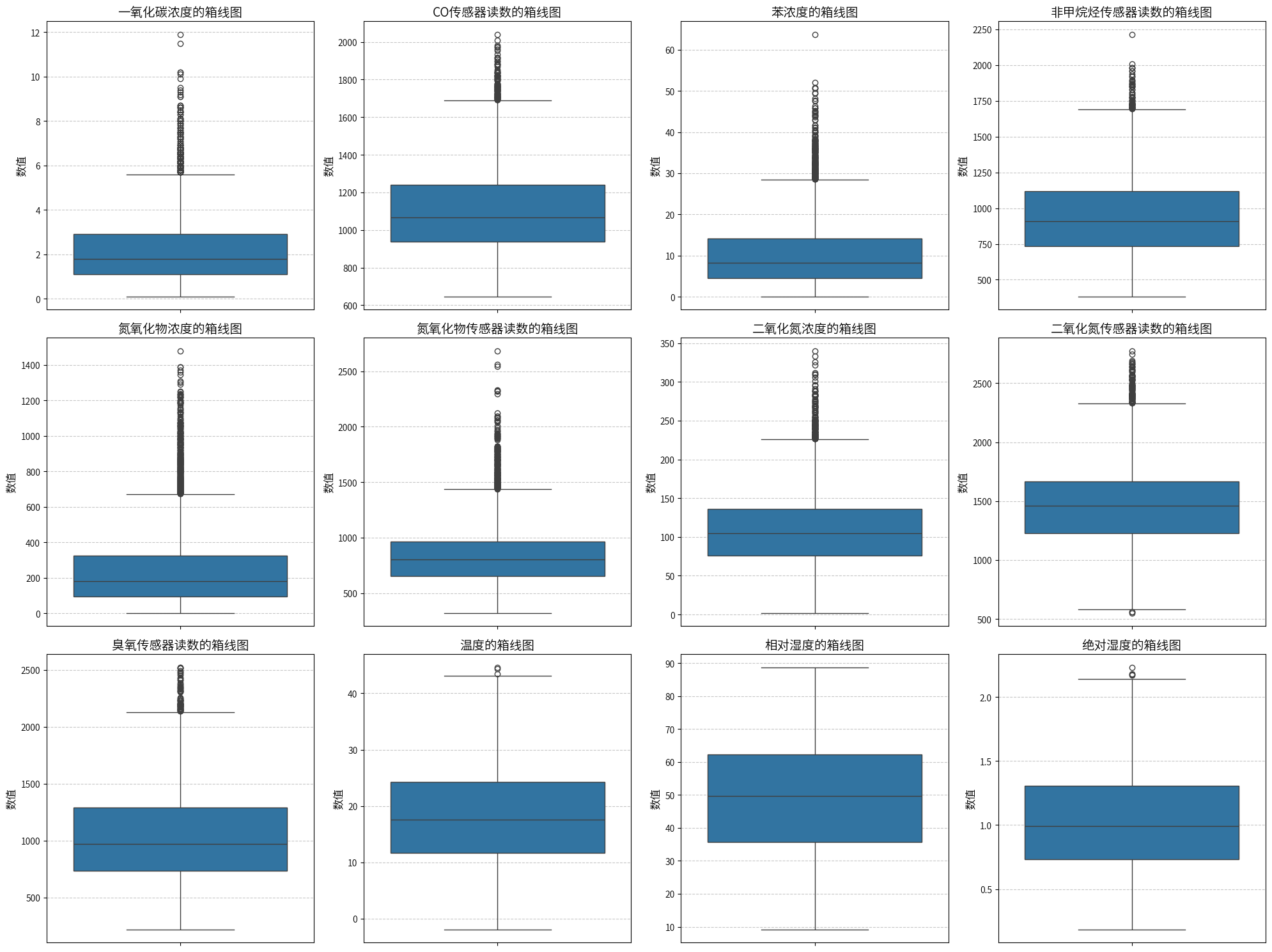
5.描述性统计

data.describe()

	Datetime	CO(GT)	PT08.S1(CO)	C6H6(GT)	PT08.S2(NMHC)	NOx(GT)	PT08.S3(NOx)	NO2(GT)	PT08.S4(NO2)	PT08.S5(O3)	T	RH	AH
count	9357	9357.000000	9357.000000	9357.000000	9357.000000	9357.000000	9357.000000	9357.000000	9357.000000	9357.000000	9357.000000	9357.000000	9357.000000
mean	2004-09-21 16:00:00	2.130603	1103.059741	10.179155	942.142620	241.922197	832.758897	109.632094	1453.298814	1032.544298	18.233408	49.191386	1.019621
min	2004-03-10 18:00:00	0.100000	647.000000	0.100000	383.000000	2.000000	322.000000	2.000000	551.000000	221.000000	-1.900000	9.200000	0.184700
25%	2004-06-16 05:00:00	1.100000	938.000000	4.500000	736.000000	96.000000	654.000000	76.000000	1227.000000	733.000000	11.700000	35.800000	0.732300
50%	2004-09-21 16:00:00	1.800000	1067.000000	8.300000	910.012987	180.000000	804.000000	104.917526	1460.000000	970.000000	17.600000	49.600000	0.989500
75%	2004-12-28 03:00:00	2.900000	1239.000000	14.100000	1119.000000	326.000000	968.000000	136.314685	1668.000000	1293.000000	24.300000	62.300000	1.306700
max	2005-04-04 14:00:00	11.900000	2040.000000	63.700000	2214.000000	1479.000000	2683.000000	340.000000	2775.000000	2523.000000	44.600000	88.700000	2.231000
std	NaN	1.431736	218.196346	7.503812	267.866611	204.315075	255.709833	46.462311	343.206131	404.447613	8.781791	17.194506	0.402203

空气污染物浓度：

样本量为 9357 条，时间跨度从 2004 年 3 月到 2005 年 4 月。
CO(GT)（一氧化碳浓度）在 0.1 至 11.9 范围内，平均 2.13，标准差为 1.43，表明在测量期间一氧化碳浓度差异较小。
C6H6(GT)（苯浓度）变化较大，范围为 0.1 至 63.7，均值为 10.18，标准差为 7.5，显示出浓度差异显著，可能受交通和工业活动影响。
NOx(GT)（氮氧化物浓度）平均 241.92，标准差 204.32，范围在 2 至 1479，表明氮氧化物浓度波动大，存在明显的高污染时段。
NO2(GT)（二氧化氮浓度）平均 109.63，标准差 46.46，分布在 2 至 340 之间，反映出浓度多在低至中等水平，但偶尔有较高浓度峰值。

传感器读数：

PT08.S1(CO) 传感器平均读数为 1103.06，范围从 647 至 2040，表明传感器对一氧化碳的检测结果变化显著。
PT08.S3(NOx) 和 PT08.S5(O3) 传感器的均值分别为 832.76 和 1032.54，标准差较大，表明氮氧化物和臭氧检测数据波动较多，可能受气象因素影响较大。

气象条件：

温度（T）：测量温度范围从 -1.9°C 到 44.6°C，均值为 18.23°C，标准差为 8.78，表明数据集覆盖了不同季节的温度变化。
相对湿度（RH）：范围为 9.2% 至 88.7%，平均湿度 49.19%，湿度分布较广，说明空气湿度有显著季节性波动。
绝对湿度（AH）：范围从 0.18 到 2.23，均值 1.02，标准差 0.40，显示空气中水分含量差异不大，稳定性相对较高。

6.空气质量聚类

# 数据标准化
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data.iloc[:, 1:])

# 使用肘部法则来确定最佳聚类数
inertia = []
silhouette_scores = []
k_range = range(2, 11)
for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=15).fit(data_scaled)
    inertia.append(kmeans.inertia_)
    silhouette_scores.append(silhouette_score(data_scaled, kmeans.labels_))

plt.figure(figsize=(15,5))

plt.subplot(1, 2, 1)
plt.plot(k_range, inertia, marker='o')
plt.xlabel('聚类中心数目')
plt.ylabel('惯性')
plt.title('肘部法则图')

plt.subplot(1, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o')
plt.xlabel('聚类中心数目')
plt.ylabel('轮廓系数')
plt.title('轮廓系数图')

plt.tight_layout()
plt.show()

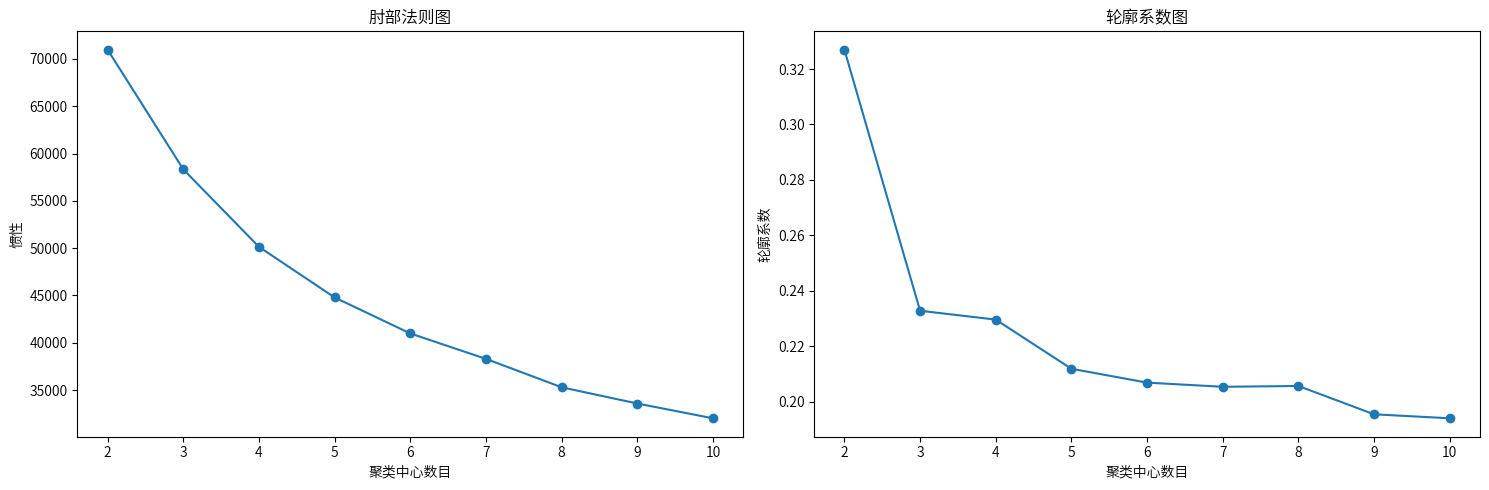
1.肘部法则（左图 - 肘部法则图）：当聚类中心数量达到 4 时，惯性值的下降幅度开始显著减小。这表明在使用 4 个聚类时，簇内误差平方和已经大幅减少，再增加聚类数所带来的改进效果逐渐减弱。
2.轮廓系数图（右图 - 轮廓系数图）：聚类数为 2 时轮廓系数最高，之后随着聚类数的增加，轮廓系数逐渐降低，尤其在 4 个聚类时仍保持在一个相对较高的水平，而之后继续增加聚类数的效果并不显著。
综上所述，4 个聚类是一个较为合理的选择，因为此时惯性值显著降低，同时轮廓系数也保持在相对较高的水平。

kmeans = KMeans(n_clusters=4, random_state=15)
kmeans.fit(data_scaled)
# 获取聚类标签
cluster_labels = kmeans.labels_
# 将聚类标签添加到原始数据中以进行分析
data['Cluster'] = cluster_labels

# 使用 PCA 将数据降维到 2 维
pca = PCA(n_components=2)
data_pca = pca.fit_transform(data_scaled)

# 将 PCA 结果转为 DataFrame，并添加聚类标签
data_pca_df = pd.DataFrame(data_pca, columns=['PCA1', 'PCA2'])
data_pca_df['Cluster'] = cluster_labels

# 绘制 PCA 降维后的聚类结果
plt.figure(figsize=(12, 8))
sns.scatterplot(x=data_pca_df['PCA1'], y=data_pca_df['PCA2'], hue=data_pca_df['Cluster'], palette='viridis', legend='full')
plt.title(f'K-Means聚类结果 - PCA 降维展示')
plt.xlabel('主成分 1 (PCA1)')
plt.ylabel('主成分 2 (PCA2)')
plt.legend(title='Cluster', loc='upper left')
plt.grid(True)
plt.show()

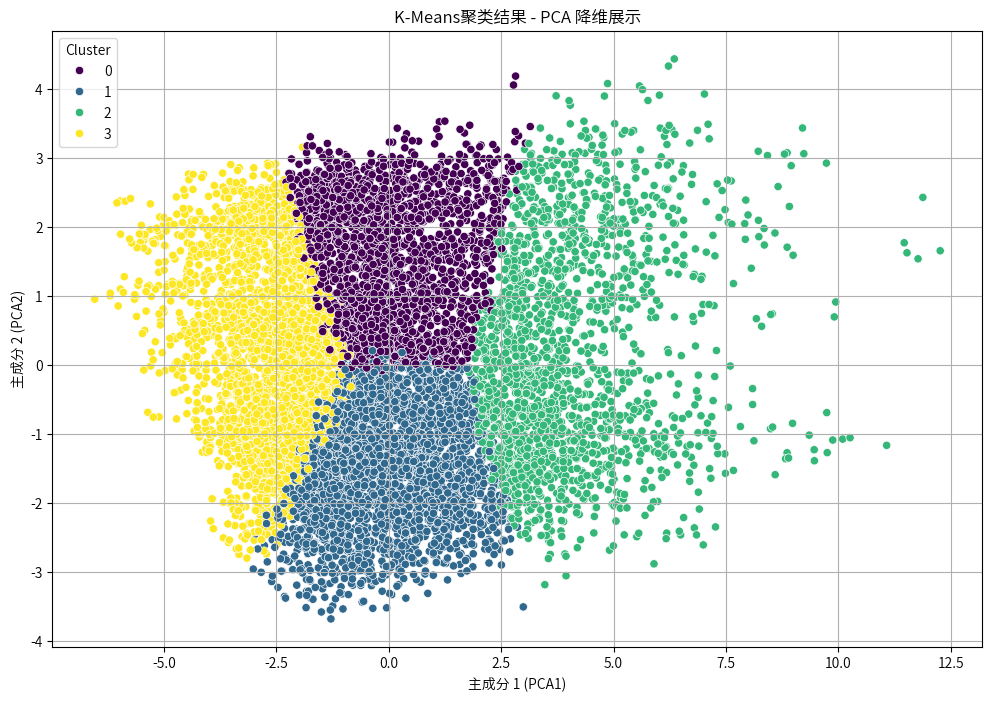
从图中可以看出，K均值聚类在这组数据上表现良好，簇的边界比较清晰，且每个簇的分布较均匀。这说明 K均值算法在此数据上确实划分出了较为合理的簇结构。

numerical_features = data.iloc[:, 1:-1].columns.tolist()
cluster_means = data.groupby('Cluster')[numerical_features].mean()

# 对每个特征进行归一化处理（每个特征单独归一化）
normalized_means = cluster_means.apply(lambda x: (x - x.min()) / (x.max() - x.min()))

plt.figure(figsize=(15, 8))
sns.heatmap(normalized_means.T, 
            cmap='coolwarm',
            center=0.5,      
            vmin=0, 
            vmax=1,
            annot=cluster_means.T.round(2),  # 显示原始值而不是归一化后的值
            fmt='.2f',
            cbar_kws={'label': '标准化得分'})

plt.xlabel('聚类')
plt.title('各聚类特征分布热力图(颜色深浅表示在该特征中的相对大小)')
plt.tight_layout()
plt.show()

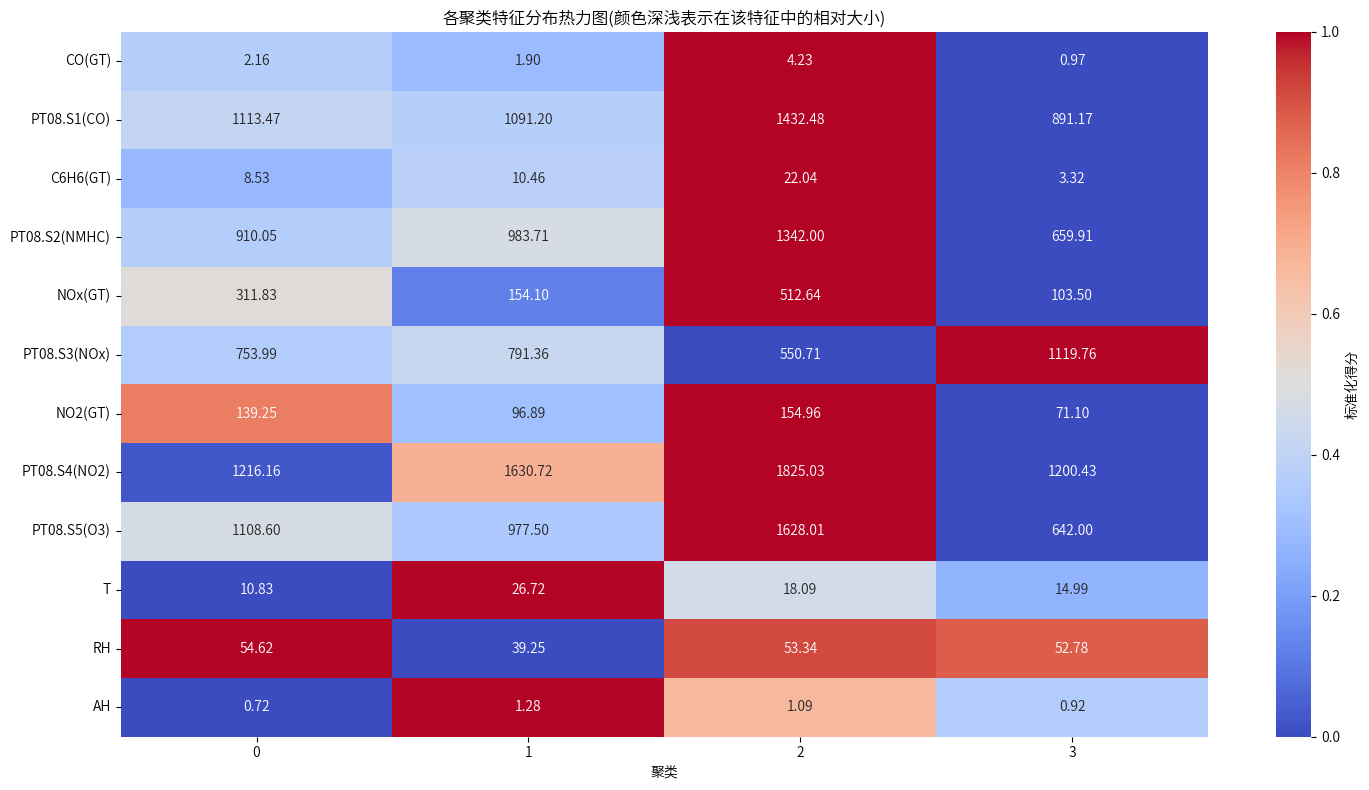
data['Datetime'] = pd.to_datetime(data['Datetime'])  # 确保 Datetime 列为日期时间格式
data['Hour'] = data['Datetime'].dt.hour  # 提取小时
data['Month'] = data['Datetime'].dt.month # 提取月份
def categorize_time_of_day(hour):
    if 0 <= hour < 6:
        return '凌晨'
    elif 6 <= hour < 12:
        return '早晨'
    elif 12 <= hour < 18:
        return '下午'
    else:
        return '晚上'
data['TimeOfDay'] = data['Hour'].apply(categorize_time_of_day)
def categorize_season(month):
    if month in [3, 4, 5]:
        return '春季'
    elif month in [6, 7, 8]:
        return '夏季'
    elif month in [9, 10, 11]:
        return '秋季'
    else:
        return '冬季'

data['Season'] = data['Month'].apply(categorize_season)

time_of_day_counts = pd.crosstab(data['Cluster'], data['TimeOfDay'])
time_of_day_proportions = pd.crosstab(data['Cluster'], data['TimeOfDay'], normalize='index')

# 创建图形
plt.figure(figsize=(12, 6))

# 使用不同的颜色
colors = ['#3498db', '#e74c3c', '#2ecc71', '#f1c40f']
bottom = np.zeros(len(time_of_day_counts))

for i, timeofday in enumerate(time_of_day_counts.columns):
   plt.bar(time_of_day_counts.index, time_of_day_counts[timeofday],
           bottom=bottom, label=timeofday, color=colors[i])
   
   for j in range(len(time_of_day_counts)):
       proportion = time_of_day_proportions.iloc[j][timeofday]
       if proportion > 0.01: # 避免为0的类型也添加标签
           y_position = bottom[j] + time_of_day_counts.iloc[j][timeofday]/2
           plt.text(j, y_position, f'{proportion:.1%}',
                   ha='center', va='center',
                   fontsize=10, color='white', fontweight='bold')
   
   bottom += time_of_day_counts[timeofday]

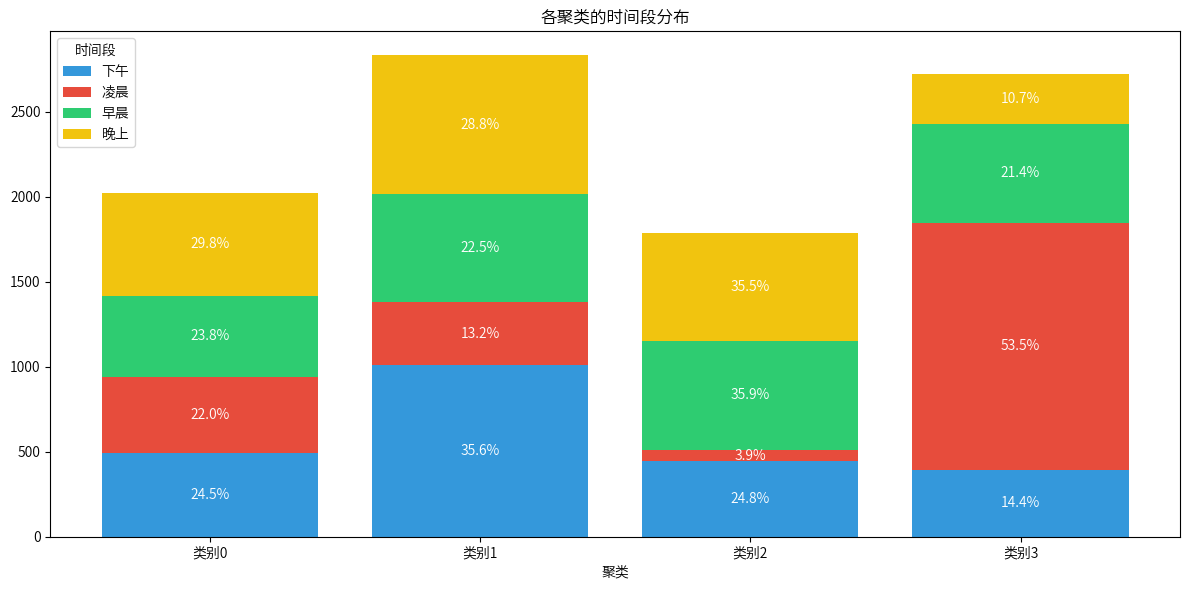
plt.title('各聚类的时间段分布')
plt.xlabel('聚类')
plt.legend(title='时间段')
plt.xticks(range(len(time_of_day_counts)), [f'类别{i}' for i in range(len(time_of_day_counts))])

plt.tight_layout()
plt.show()

Season_counts = pd.crosstab(data['Cluster'], data['Season'])
Season_proportions = pd.crosstab(data['Cluster'], data['Season'], normalize='index')

# 创建图形
plt.figure(figsize=(12, 6))

# 使用不同的颜色
colors = ['#3498db', '#e74c3c', '#2ecc71', '#f1c40f']
bottom = np.zeros(len(Season_counts))

for i, sn in enumerate(Season_counts.columns):
   plt.bar(Season_counts.index, Season_counts[sn],
           bottom=bottom, label=sn, color=colors[i])
   
   for j in range(len(Season_counts)):
       proportion = Season_proportions.iloc[j][sn]
       if proportion > 0.01: # 避免为0的类型也添加标签
           y_position = bottom[j] + Season_counts.iloc[j][sn]/2
           plt.text(j, y_position, f'{proportion:.1%}',
                   ha='center', va='center',
                   fontsize=10, color='white', fontweight='bold')
   
   bottom += Season_counts[sn]

plt.title('各聚类的季节分布')
plt.xlabel('聚类')
plt.legend(title='季节')
plt.xticks(range(len(Season_counts)), [f'类别{i}' for i in range(len(Season_counts))])

plt.tight_layout()
plt.show()

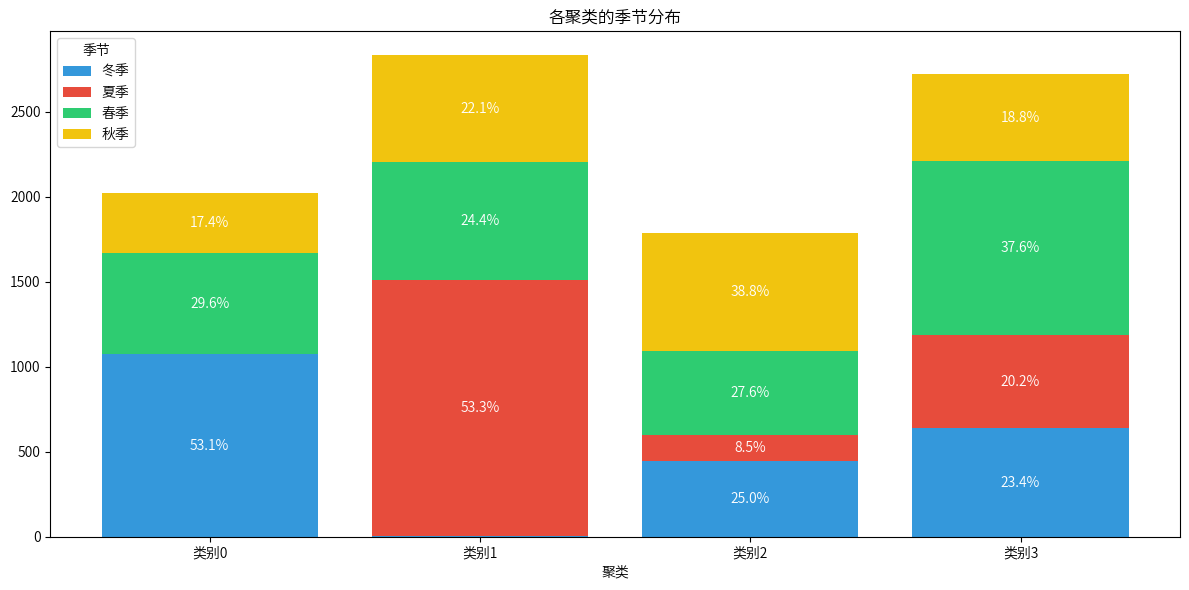
Cluster 0: 较高的一氧化碳 (CO) 和氮氧化物 (NOx) 水平，温度较低，湿度较高，记录集中在晚上和下午，主要出现在冬季。

Cluster 1: 较低的一氧化碳 (CO) 和苯 (C6H6) 水平，温度较高，湿度较低，记录集中在下午和晚上，主要出现在夏季。

Cluster 2: 较高的一氧化碳 (CO)、苯 (C6H6) 和氮氧化物 (NOx) 水平，温度适中，湿度较高，记录集中在早晨和晚上，主要出现在秋季。

Cluster 3: 较低的污染物水平，温度适中，湿度较高，记录集中在凌晨和早晨，主要出现在春季。

7.关联规则分析

7.1数据预处理

将污染物浓度数据转换为适合进行关联规则分析的形式，通常需要将数值数据离散化为不同的区间，将污染物浓度划分成低、中、高三个区间。

# 等频分箱处理函数
def discretize_column_equal_freq(column):
    return pd.qcut(column, q=3, labels=['低', '中', '高'])

# 离散化污染物数据
pollutants = ['CO(GT)', 'C6H6(GT)', 'NOx(GT)', 'NO2(GT)', 'T', 'RH', 'AH']
association_data = data.copy()
for pollutant in numerical_features:
    if pollutant in data.columns:
        association_data[pollutant + '_level'] = discretize_column_equal_freq(association_data[pollutant])

# 创建用于关联规则分析的数据集，选择只包含污染物等级的列
association_data = association_data[[pollutant + '_level' for pollutant in numerical_features if pollutant + '_level' in association_data.columns]]
# 将数据转化为适合Apriori算法的布尔型数据格式
# 对每个污染物的浓度等级进行One-Hot编码处理（每列代表一个污染物浓度等级的存在与否）
association_data = association_data.apply(lambda x: x == '高', axis=0)

7.2Apriori算法

# 使用Apriori算法提取频繁项集
frequent_itemsets = apriori(association_data, min_support=0.01, use_colnames=True)

# 生成关联规则
rules = association_rules(frequent_itemsets, metric="lift", min_threshold=1, num_itemsets=2)

# 查看前几个关联规则
print(rules.head())

           antecedents            consequents  antecedent support  \
0  (PT08.S1(CO)_level)         (CO(GT)_level)            0.333013   
1       (CO(GT)_level)    (PT08.S1(CO)_level)            0.333333   
2     (C6H6(GT)_level)         (CO(GT)_level)            0.332799   
3       (CO(GT)_level)       (C6H6(GT)_level)            0.333333   
4       (CO(GT)_level)  (PT08.S2(NMHC)_level)            0.333333   

   consequent support   support  confidence      lift  representativity  \
0            0.333333  0.255851    0.768293  2.304878               1.0   
1            0.333013  0.255851    0.767554  2.304878               1.0   
2            0.333333  0.264401    0.794477  2.383430               1.0   
3            0.332799  0.264401    0.793203  2.383430               1.0   
4            0.332692  0.264294    0.792882  2.383232               1.0   

   leverage  conviction  zhangs_metric   jaccard  certainty  kulczynski  
0  0.144847    2.877193       0.848798  0.623275   0.652439    0.767923  
1  0.144847    2.869425       0.849206  0.623275   0.651498    0.767923  
2  0.153468    3.243750       0.869958  0.658154   0.691715    0.793840  
3  0.153468    3.226357       0.870655  0.658154   0.690053    0.793840  
4  0.153397    3.221878       0.870603  0.657888   0.689622    0.793646

# 绘制支持度、置信度、提升度的分布图
plt.figure(figsize=(12, 6))

# 绘制支持度分布图
plt.subplot(1, 3, 1)
plt.hist(rules['support'], bins=20, color='skyblue', edgecolor='black')
plt.title('支持度分布')
plt.xlabel('支持度')
plt.ylabel('频次')

# 绘制置信度分布图
plt.subplot(1, 3, 2)
plt.hist(rules['confidence'], bins=20, color='lightgreen', edgecolor='black')
plt.title('置信度分布')
plt.xlabel('置信度')
plt.ylabel('频次')

# 绘制提升度分布图
plt.subplot(1, 3, 3)
plt.hist(rules['lift'], bins=20, color='salmon', edgecolor='black')
plt.title('提升度分布')
plt.xlabel('提升度')
plt.ylabel('频次')

plt.tight_layout()
plt.show()

Support（支持度）：规则在数据集中出现的频率。例如，如果规则 A -> B 的支持度为 0.3，表示 30% 的数据记录符合该规则。
Confidence（置信度）：给定前提（Antecedent）发生时，后果（Consequent）发生的概率。例如，CO(GT)_level -> PT08.S1(CO)_level 规则的置信度为 0.76，表示在 CO(GT)_level 为高的情况下，PT08.S1(CO)_level 高的概率为 76%。
Lift（提升度）：衡量规则的有效性，通常用于评估关联的强度。提升度大于 1 表示规则比随机情况下发生的概率更高，越大表示规则越强。

# 筛选出支持度大于0.15，置信度大于0.8，提升度大于2的规则
high_quality_rules = rules[(rules['support'] > 0.15) & (rules['confidence'] > 0.8) & (rules['lift'] > 2)]

# 按照lift降序排序规则，以找到最强的关联
high_quality_rules_sorted = high_quality_rules.sort_values(by='lift', ascending=False)
high_quality_rules_sorted

	antecedents	consequents	antecedent support	consequent support	support	confidence	lift	representativity	leverage	conviction	zhangs_metric	jaccard	certainty	kulczynski
16105	(PT08.S1(CO)_level, NOx(GT)_level, PT08.S2(NMH...	(C6H6(GT)_level, CO(GT)_level, PT08.S5(O3)_level)	0.185209	0.235332	0.170033	0.918061	3.901135	1.0	0.126448	9.332183	0.912706	0.678754	0.892844	0.820293
16094	(PT08.S1(CO)_level, C6H6(GT)_level, NOx(GT)_le...	(CO(GT)_level, PT08.S5(O3)_level, PT08.S2(NMHC...	0.185743	0.235225	0.170033	0.915420	3.891679	1.0	0.126342	9.042034	0.912540	0.677598	0.889405	0.819137
16414	(PT08.S1(CO)_level, NO2(GT)_level, PT08.S2(NMH...	(C6H6(GT)_level, CO(GT)_level, PT08.S5(O3)_level)	0.174629	0.235332	0.157957	0.904529	3.843631	1.0	0.116861	8.009409	0.896359	0.626802	0.875147	0.787868
16403	(PT08.S1(CO)_level, C6H6(GT)_level, NO2(GT)_le...	(CO(GT)_level, PT08.S5(O3)_level, PT08.S2(NMHC...	0.175163	0.235225	0.157957	0.901769	3.833647	1.0	0.116754	7.785505	0.896119	0.625741	0.871556	0.786641
16102	(NOx(GT)_level, PT08.S5(O3)_level, PT08.S2(NMH...	(PT08.S1(CO)_level, C6H6(GT)_level, CO(GT)_level)	0.192476	0.232981	0.170033	0.883398	3.791723	1.0	0.125190	6.578104	0.911760	0.665690	0.847981	0.806607
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
21	(PT08.S2(NMHC)_level)	(PT08.S1(CO)_level)	0.332692	0.333013	0.267821	0.805011	2.417359	1.0	0.157030	3.420645	0.878643	0.673113	0.707657	0.804624
20	(PT08.S1(CO)_level)	(PT08.S2(NMHC)_level)	0.333013	0.332692	0.267821	0.804236	2.417359	1.0	0.157030	3.408740	0.879065	0.673113	0.706636	0.804624
1439	(NOx(GT)_level, CO(GT)_level)	(C6H6(GT)_level, PT08.S2(NMHC)_level)	0.235866	0.332051	0.189163	0.801994	2.415273	1.0	0.110844	3.373372	0.766840	0.499436	0.703561	0.685838
143	(NOx(GT)_level, CO(GT)_level)	(C6H6(GT)_level)	0.235866	0.332799	0.189377	0.802900	2.412567	1.0	0.110881	3.385087	0.766232	0.499296	0.704587	0.685971
184	(NOx(GT)_level, CO(GT)_level)	(PT08.S2(NMHC)_level)	0.235866	0.332692	0.189163	0.801994	2.410618	1.0	0.110692	3.370134	0.765793	0.498592	0.703276	0.685289

570 rows × 14 columns

# 可视化支持度、置信度和提升度的散点图
plt.figure(figsize=(10, 6))
plt.scatter(high_quality_rules_sorted['support'], high_quality_rules_sorted['confidence'], 
            c=high_quality_rules_sorted['lift'], cmap='viridis', edgecolors='k', s=100, alpha=0.7)

# 添加标题和标签
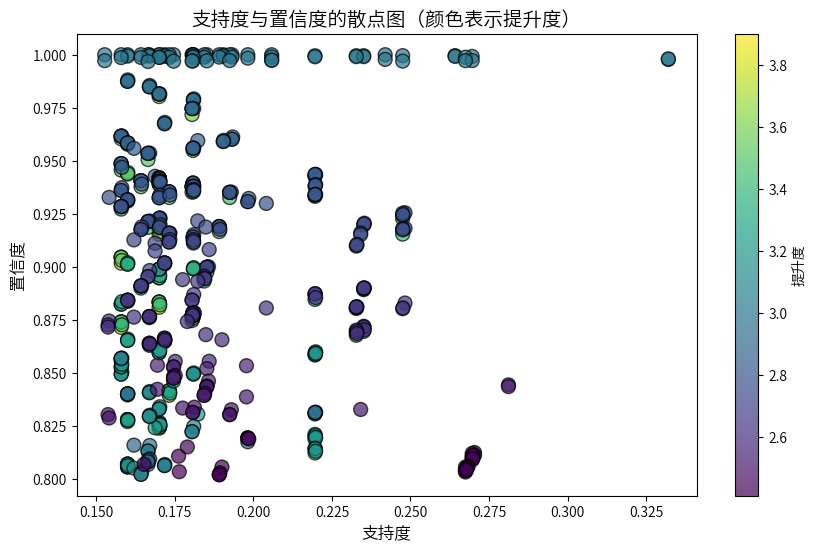
plt.title('支持度与置信度的散点图（颜色表示提升度）', fontsize=14)
plt.xlabel('支持度', fontsize=12)
plt.ylabel('置信度', fontsize=12)
plt.colorbar(label='提升度')  # colorbar for lift
plt.show()

# 可视化提升度最高的前10条规则的条形图
top_10_rules_by_lift = high_quality_rules_sorted.head(10)
plt.figure(figsize=(10, 6))
sns.barplot(x='lift', y='antecedents', data=top_10_rules_by_lift, hue='antecedents', palette='viridis', legend=False)

# 添加标题和标签
plt.title('提升度最高的前10条规则', fontsize=14)
plt.xlabel('提升度', fontsize=12)
plt.ylabel('前置条件', fontsize=12)
plt.show()

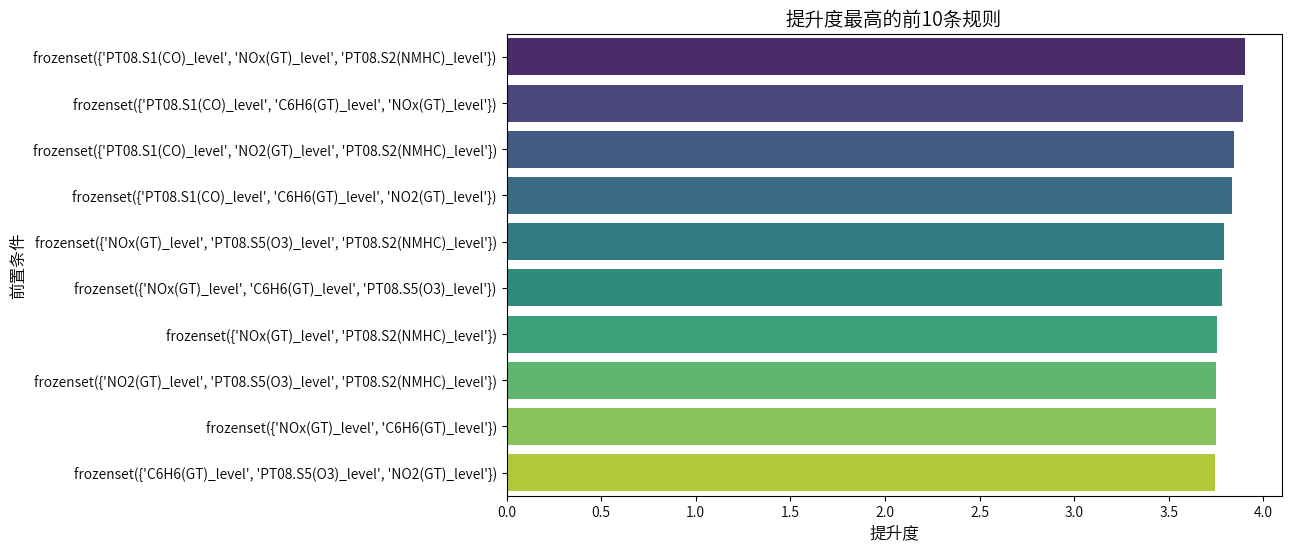
将支持度阈值设为 0.15、置信度设为 0.8、提升度设为 2 如此严格的要求下，还是筛选出大量比较稳定的规则，根据提升度排序，用Chat-GPT 4o 总结了前五条规则（文件路径在/home/mw/project里面）：

规则 1:
- 前置条件：NOx(GT)_level 和 PT08.S1(CO)_level
- 后置条件：C6H6(GT)_level、CO(GT)_level 和 PT08.S4(NO2)_level
- 支持度：0.170
- 置信度：0.918
- 提升度：3.90
解读：当 NOx(GT)_level 和 PT08.S1(CO)_level 为高浓度时，C6H6(GT)_level、CO(GT)_level 和 PT08.S4(NO2)_level 也通常处于高浓度。这个规则的提升度接近 4，表示这种组合的关联性非常强。
规则 2:
- 前置条件：NOx(GT)_level 和 PT08.S1(CO)_level
- 后置条件：PT08.S2(NMHC)_level 和 CO(GT)_level
- 支持度：0.170
- 置信度：0.915
- 提升度：3.89
解读：当 NOx(GT)_level 和 PT08.S1(CO)_level 为高浓度时，PT08.S2(NMHC)_level 和 CO(GT)_level 通常也为高浓度，提升度为 3.89。这表明 NOx 和 CO 之间的关联度较高。
规则 3:
- 前置条件：PT08.S1(CO)_level 和 PT08.S2(NMHC)_level
- 后置条件：C6H6(GT)_level、CO(GT)_level 和 PT08.S4(NO2)_level
- 支持度：0.158
- 置信度：0.905
- 提升度：3.84
解读：当 PT08.S1(CO)_level 和 PT08.S2(NMHC)_level 为高时，C6H6(GT)_level、CO(GT)_level 和 PT08.S4(NO2)_level 也往往是高浓度，关联性强，提升度为 3.84。
规则 4:
- 前置条件：PT08.S1(CO)_level 和 C6H6(GT)_level
- 后置条件：PT08.S2(NMHC)_level 和 CO(GT)_level
- 支持度：0.158
- 置信度：0.902
- 提升度：3.83
解读：当 PT08.S1(CO)_level 和 C6H6(GT)_level 都为高时，PT08.S2(NMHC)_level 和 CO(GT)_level 也很可能为高，表明 CO 与 C6H6 之间存在显著关联。
规则 5:
- 前置条件：NOx(GT)_level 和 PT08.S2(NMHC)_level
- 后置条件：PT08.S1(CO)_level 和 C6H6(GT)_level
- 支持度：0.170
- 置信度：0.883
- 提升度：3.79
解读：当 NOx(GT)_level 和 PT08.S2(NMHC)_level 都为高时，PT08.S1(CO)_level 和 C6H6(GT)_level 也通常为高。这说明 NOx 和 CO 之间的读数在空气污染监测中可能有密切关系。

8.空气质量等级分类

空气质量指数（AQI）通常基于以下几种常见的污染物浓度：PM2.5、PM10、CO（一氧化碳）、SO2（二氧化硫）、NO2（二氧化氮）、O3（臭氧）
数据集中包含 CO(GT)、NOx(GT)、NO2(GT) 和 PT08.S5(O3)，可以分别代表一氧化碳（CO）、氮氧化物（NOx）、二氧化氮（NO2）和臭氧（O3）的浓度。
每个污染物浓度需要转换为 IAQI（Individual Air Quality Index，个体空气质量指数），然后取所有 IAQI 的最大值作为 AQI。

$IAQI_P = \frac{IAQI_{Hi} - IAQI_{Lo}}{BP_{Hi} - BP_{Lo}} \times (C_P - BP_{Lo}) + IAQI_{Lo}$
其中， $C_P$ 是污染物的实测浓度， $BP_{Hi}$ 和 $BP_{Lo}$ 是该浓度段的上下限， $IAQI_{Hi}$ 和 $IAQI_{Lo}$ 是对应的 IAQI 范围。

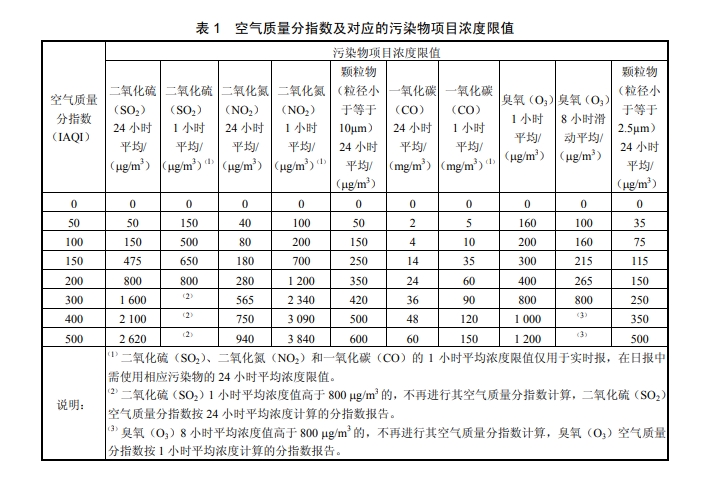
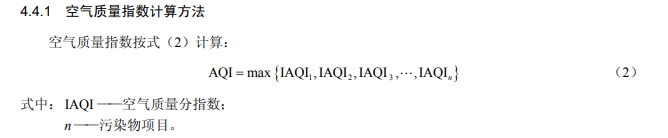
Image Name

图片和公式均来自环境空气质量指数（AQI）技术规定（试行）（HJ 633—2012 ）

# IAQI 计算函数
def calculate_iaqi(concentration, breakpoints):
    for (low, high, iaqi_low, iaqi_high) in breakpoints:
        if low <= concentration <= high:
            return iaqi_low + (iaqi_high - iaqi_low) * (concentration - low) / (high - low)
    return None  # 如果不在范围内则返回None

IAIQ_data = data.copy()

# 定义 CO, NO2, NOx, O3 的 IAQI 分段表
co_breakpoints = [(0, 5, 0, 50), (5, 10, 51, 100), (10, 35, 101, 150), (35, 60, 151, 200), (60, 90, 201, 300), (90, float('inf'), 301, 500)]
no2_breakpoints = [(0, 40, 0, 50), (40, 80, 51, 100), (80, 180, 101, 150), (180, 280, 151, 200), (280, 565, 201, 300), (565, float('inf'), 301, 500)]
nox_breakpoints = no2_breakpoints  # NOx 和 NO2 使用相同的 IAQI 分段
o3_breakpoints = [(0, 100, 0, 50), (100, 160, 51, 100), (160, 215, 101, 150), (215, 265, 151, 200), (265, 800, 201, 300), (800, float('inf'), 301, 500)]

# 应用 IAQI 计算
IAIQ_data['IAQI_CO'] = IAIQ_data['CO(GT)'].apply(lambda x: calculate_iaqi(x, co_breakpoints))
IAIQ_data['IAQI_NO2'] = IAIQ_data['NO2(GT)'].apply(lambda x: calculate_iaqi(x, no2_breakpoints))
IAIQ_data['IAQI_NOx'] = IAIQ_data['NOx(GT)'].apply(lambda x: calculate_iaqi(x, nox_breakpoints))
IAIQ_data['IAQI_O3'] = IAIQ_data['PT08.S5(O3)'].apply(lambda x: calculate_iaqi(x, o3_breakpoints))

# 计算 AQI
data['AQI'] = IAIQ_data[['IAQI_CO', 'IAQI_NO2', 'IAQI_NOx', 'IAQI_O3']].max(axis=1)

# 根据 AQI 划分空气质量等级
def classify_aqi(aqi):
    if aqi <= 50:
        return '优'
    elif aqi <= 100:
        return '良'
    elif aqi <= 150:
        return '轻度污染'
    elif aqi <= 200:
        return '中度污染'
    elif aqi <= 300:
        return '重度污染'
    else:
        return '严重污染'

data['AQI等级'] = data['AQI'].apply(classify_aqi)

# 计算每个 AQI 等级的频次分布
aqi_counts = data['AQI等级'].value_counts().sort_index()

# 创建 AQI 等级分布的条形图
plt.figure(figsize=(10, 6))
sns.countplot(data=data, x='AQI等级', order=['优', '良', '轻度污染', '中度污染', '重度污染', '严重污染'], palette='viridis', hue='AQI等级', legend=False)
plt.title('空气质量等级的分布')
plt.xlabel('空气质量等级')
plt.ylabel('频次')
plt.show()

Image Name

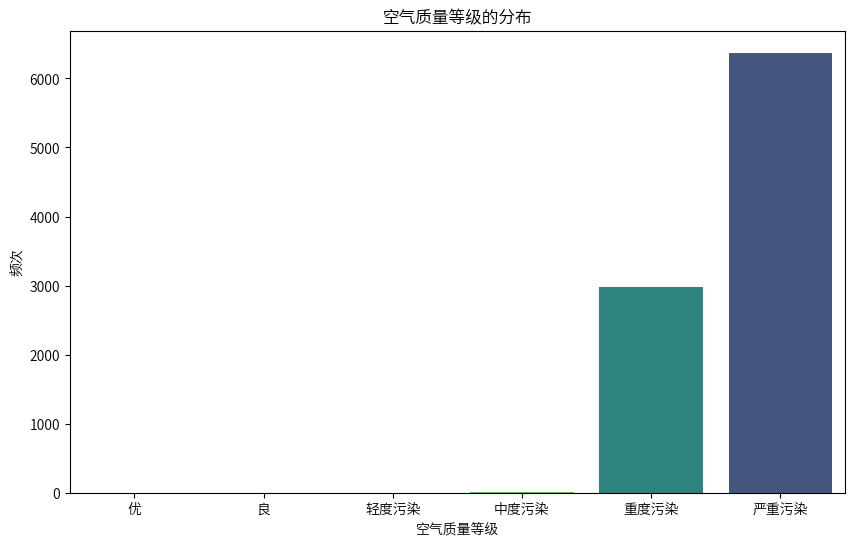
看样子这一年的污染是特别严重的，通过查阅数据集来源，发现该数据的测量设备位于意大利一个城市内一个严重污染区域的田野上，这也就说得清楚了。

9.结论

基于对 2004 年 3 月至 2005 年 4 月空气质量数据的深入分析，本项目得出以下主要结论：
1.基于K-Means聚类得到四种聚类情况：
Cluster 0: 较高的一氧化碳 (CO) 和氮氧化物 (NOx) 水平，温度较低，湿度较高，记录集中在晚上和下午，主要出现在冬季。
Cluster 1: 较低的一氧化碳 (CO) 和苯 (C6H6) 水平，温度较高，湿度较低，记录集中在下午和晚上，主要出现在夏季。
Cluster 2: 较高的一氧化碳 (CO)、苯 (C6H6) 和氮氧化物 (NOx) 水平，温度适中，湿度较高，记录集中在早晨和晚上，主要出现在秋季。
Cluster 3: 较低的污染物水平，温度适中，湿度较高，记录集中在凌晨和早晨，主要出现在春季。

2.关联规则分析揭示了关键污染物关联关系：
通过 Apriori 关联规则挖掘，发现了污染物之间的显著关联。例如，NOx(GT)_level 和 CO(GT)_level 高浓度状态下，往往伴随 PT08.S1(CO)_level 和 C6H6(GT)_level 的高浓度。这些关联关系暗示了特定污染源（如交通排放和工业活动）对多种污染物的共同影响。

3.空气质量指数（AQI）分析揭示污染水平动态变化：
通过对污染物浓度计算 AQI，数据集中 AQI 指数多数处于“轻度污染”到“重度污染”水平，这表明数据采集地点处于严重污染区域。

4.实践建议：

加强交通和工业排放控制：通过监测 NOx 和 CO 水平，尤其在冬季和交通高峰期，适时实施限行政策，减少高污染时段的污染源排放。
优化污染物监测策略：重点关注 NOx 和 CO 等主要污染物，建立完善的空气质量监测网络，实时跟踪空气质量变化，提供预警服务。
改善公众健康防护措施：建议敏感人群减少户外活动，提供空气质量预警并推广防护措施，如佩戴口罩、使用空气净化器等。
引导公众养成良好的生活习惯：在空气质量较差的时段，减少户外运动及污染性活动，增强公众环保意识，以个人行为减少空气污染。

原文地址：https://blog.csdn.net/m0_53814833/article/details/143777431

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！

上一篇：Stable Diffusion概要讲解
下一篇：【Rust中的策略模式实现】

二维费用背包问题
还是分为选和不选第 i 个元素，如果不选就是继承上一个状态 dp[i - 1][j][k]，如果选，由于总人数不能超过 j ，是需要 j >= g[i] 的，也就是 j - g[i] 不能小于
阅读更多2024-11-19
LeetCode17：电话号码的字母组合
这个题目也就是先使用一个映射定义好字符与数字的映射关系，然后再根据回溯三部曲来去写这个题目。
阅读更多2024-11-19
TypeScript中泛型的详细介绍
在TypeScript（TS）中，泛型（Generics）是一种强大的特性，它允许在定义函数、接口或类时不预先指定具体的类型，而是在使用的时候再指定类型。这种参数化类型的方式使得代码更加灵活和可复用。
阅读更多2024-11-19
String类型
regionMatches` 是 Java 中 `String` 类的一个方法，它用于比较两个字符串在指定区域内的子串是否相等。类的行为都是非法的。- 返回值：一个整数，表示调用该方法
阅读更多2024-11-19
大模型呼叫中心，如何建设坐席辅助系统？
综上所述，建设大模型呼叫中心坐席辅助系统需要综合考虑多个方面，从需求分析和设计到系统上线运行和优化升级，每个步骤都至关重要。通过选择合适的系统解决方案、配置高性能的硬件设备、集成先进的软件系统以及持续
阅读更多2024-11-19
《生成式 AI》课程第4講：訓練不了人工智慧？你可以訓練你自己 (中)
这一系列的作业是为 2024 年春季的《生成式 AI》课程设计的，共包含十个作业。每个作业都对应一个具体的主题，例如真假难辨的世界、AI 应用开发、AI催眠大师、LLM 微调等。承接上一讲：《生成式
阅读更多2024-11-19
【C++】哈希表的实现详解
在顺序结构以及平衡树中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素时，必须要经过关键码的多次比较。顺序查找时间复杂度为O(N)，平衡树中为树的高度，即O(logN)，搜索的效率决于搜
阅读更多2024-11-19
Leetcode 有效的数独
这段代码解决的是的问题，其算法思想是基于。falsetrue。
阅读更多2024-11-19
小林Coding—Java「五、Java虚拟机面试篇」
小林Coding—Java「五、Java虚拟机面试篇」笔记整理
阅读更多2024-11-19
一个简单的图像分类项目（九）并行训练的学习：多GPU的DP（DataParallel数据并行）
将电脑装成Ubuntu、Windows双系统，并在Ubuntu上继续学习。在现代深度学习中，多主机多GPU训练已经变得非常常见，尤其是对于大规模模型和数据集。最简单和早期的并行计算比如NVIDIA的S
阅读更多2024-11-19