蒙提霍尔问题
1.简介
蒙提霍尔问题(Monty Hall problem)是美国电视游戏节目《Let’s Make a Deal》中的一个问题,并以主持人 Monty Hall 命名。
蒙提霍尔问题也叫「三门问题」或「山羊汽车问题」。
假设您正在参加一个游戏节目,并且您可以选择三扇门:一扇门后面是一辆汽车;另外两扇门后面是山羊。 你选择一扇门,比如 1 号门。主人知道门后有什么,他会打开另外两扇门中是山羊的门,比如 3 号门。 然后他对你说:“你想选2号门吗?” 改变选择对你有利吗?
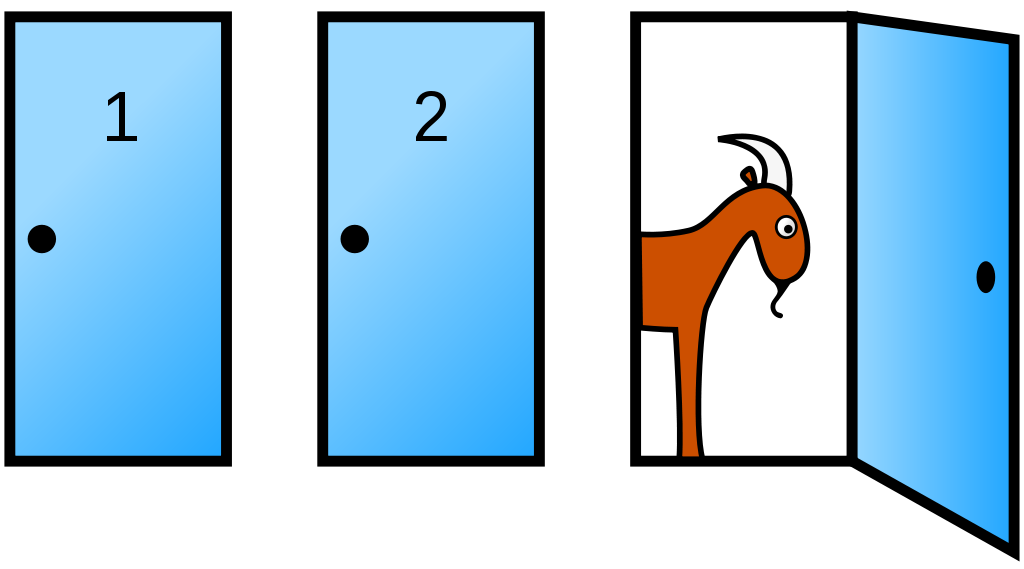
2.答案
应该换,因为不换选中汽车的概率是 1/3,交换后获得汽车的概率是 2/3。
下面以穷举的方式证明上面的答案。
总共有三种可能情况,每种情况的可能性均是 1/3:
- 参赛者挑汽车,主持人挑两头羊的任何一头。交换将失败。
- 参赛者挑A羊,主持人挑B羊。交换将赢得汽车。
- 参赛者挑B羊,主持人挑A羊。交换将赢得汽车。
所以选择交换获得汽车的概率是 2/3,不交换获得汽车的概率是 1/3。

或者简单的解释为,最初选择的门后是汽车的概率为 1/3,那么在剩下的两个门中,有汽车的概率是 2/3。在剩下的两个门中,排除掉一个门后,剩下的那个门后为汽车的概率依旧是 2/3,所以应该交换。
3.直觉的错误
很多人第一次遇到这个问题时,直觉上会认为汽车在剩下的两个门后面的概率均为 1/2,所以换与不换没有区别。
三门问题和三囚问题很类似,直觉上也会产生错误。
一个国家的大理寺诏狱中有甲、乙、丙三个政治犯死囚,新任皇帝决定在亲政之日特赦其中一位囚犯作为庆祝;但要在同日将另两位斩首,以正国法。皇帝抽签选出那位幸运的囚犯之后,签署了特赦令,告诉大理正卿,哪两位囚犯将要被处决,哪一位囚犯将要被赦免。但皇帝特别要求正卿,不可让死囚知晓自己即将被处死或被特赦,以免影响囚情。甲听闻了皇帝即将赦免三人中的一人,赶紧私下向正卿询问自己未来的情况,正卿却答:“奉上谕,我不能让你知道,你会被赦免或者处决。所以我只告诉你,另外两人之中,其中一人会遭处决。
甲听后非常高兴,认为现在只有自己跟乙或丙其中一人可能会被赦免,所以自己有五成的机会被赦免,甲高兴地一五一十地告诉了大理评事,评事却说:“不对,你只有三分之一的机会。”究竟何者为真呢?
“三门问题”其实跟“三囚问题”道理是一样的。“三个死囚”就是“三扇门”,“特赦令”就是“车”,“被斩首”就是“羊”。
因为特赦令是在三个死囚中产生的,所以每个死囚获得特赦令的概率各是 1/3。之所以甲认为其获得特赦的概率是 1/2,因为他认为特赦令是在排除乙丙某人后,再由皇帝选择二者其中一人特赦。但事实并非如此,皇帝是在三人中选一人,而非两人中选一人特赦。
参考文献
Monty Hall problem - wikipedia
原文地址:https://blog.csdn.net/K346K346/article/details/136403588
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
