计算机数制转换
一.计算机的数制
1.十进制:每一位可取0~9这十个数码,计数的基数为10,超过9须用多位数来表示。
2.二进制:每一位可取0~1这2个数码,计数的基数为2,超过1须用多位数来表示。
3.八进制:每一位可取0~7这8个数码,计数的基数为8,超过7须用多位数来表示。
4.十六进制:每一位可取0~9,A,B,C,D,E,F这16个数码,计数的基数为16,超过F须用多位数来表示。
5.权:数制中某一位上的1所表示的数值的大小。例如,十进制123,1的位权是100,2的位权是10,3的位权是1。
| 2(B) | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8(O) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 10(D) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16(H) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
二.各种数制之间的转换
1.K进制转十进制
按权相加法展开成一个多项式,每项是该位的数码与相应的权之积,把多项式按十进制数的规则进行求和,所得结果即是该数的十进制。
公式:abcd.efg(K)=d*K^0+c*K^1+b*K^2+a*k^3+e*K^-1+f*K^-2+g*K^-3(10)
例:1101.01(2)=1*2^0+0*2^1+1*2^2+1*2^3+0*2^-1+1*2^-2=1+0+4+8+0+0.25=13.25(10)
2.十进制转K进制
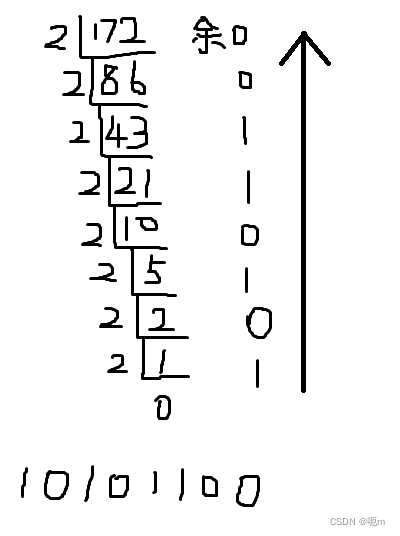
整数部分:十进制整数转化为K进制整数的方法是倒除法,即除K直至商为0,倒取余数。
例:172(10)=10101100(2)
注:
小数部分:十进制小数转换为K进制小数的方法是取整法,即小数部分循环乘K直至为0,顺序取整数部分。
例:0.625(10)=0.101(2)
0.625*2=1.25-------取出整数部分1
0.25*2=0.5----------取出整数部分0
0.5*2=1.0------------取出整数部分1
3.二进制转八进制
整数部分:从右向左,二进制3位一组转成八进制。
小数部分:从左向右,二进制3位一组转成八进制。
注:如果不足3位可补0。
例:1 111 010 101 101(2)=17255(8)
例:1 101 110.101 1(2)=156.54(8)
另外,二进制也可以先转成十进制,再由十进制转成八进制。
4.二进制转十六进制
整数部分:从右向左,二进制4位一组转成十六进制。
小数部分:从左向右,二进制4位一组转成十六进制。
注:如果不足4位可补0。
例:1 1110 1010 1101(2)=1EAD(16)
例:1 1110 1001.1011 1(2)=1E9.B8(16)
(以上除注外为摘录《信息学奥赛一本通 初赛真题解析》第一章第5节 数制转换)
原文地址:https://blog.csdn.net/D_31415926/article/details/137995287
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
