[AIZU ONLINE JUDGE] 计算几何 CGL_4_C (切割凸包)
Convex Cut
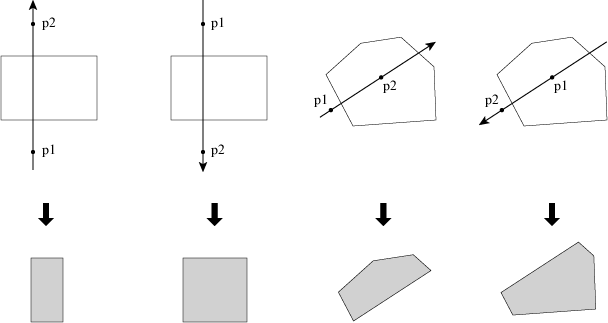
As shown in the figure above, cut a convex polygon g by a line p1p2 and print the area of the cut polygon which is on the left-hand side of the line.
g is represented by a sequence of points p1, p2,..., pn where line segments connecting pi and pi+1 (1 ≤ i ≤ n−1) are sides of the convex polygon. The line segment connecting pn and p1 is also a side of the polygon.
Input
The input is given in the following format:
g (the sequence of the points of the polygon) q (the number of queries = the number of target lines) 1st query 2nd query : qth query
g is given as a sequence of points p1,..., pn in the following format:
n x1 y1 x2 y2 : xn yn
The first integer n is the number of points. The coordinate of the i-th point pi is given by two integers xi and yi. The coordinates of points are given in the order of counter-clockwise visit of them. Note that all interior angles of given convex polygons are less than or equal to 180.
For each query, a line represented by two points p1 and p2 is given. The coordinates of the points are given by four integers p1x, p1y, p2x and p2y.
Output
For each query, print the area of the cut polygon. The output values should be in a decimal fraction with an error less than 0.00001.
Constraints
- 3 ≤ n ≤ 100
- 1 ≤ q ≤ 100
- -10000 ≤ xi, yi ≤ 10000
- -10000 ≤ p1x,p1y,p2x,p2y ≤ 10000
- No point in g will occur more than once.
- p1 ≠ p2
Sample Input
4 1 1 4 1 4 3 1 3 2 2 0 2 4 2 4 2 0
Sample Output
2.00000000 4.00000000
题意:
如图所示,给出一个凸多边形,并给出一条由p1 -> p2的有向直线,将凸多边形切割成两部分,求解凸多边形再有向直线左半部分的面积,小数点后保留8位小数。
题解:
思路很简单,求出直线与凸包的两个交点,并将有向直线左边的点全部纳入数组中,对这个点集所组成的凸多边形求解面积即可。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const double eps = 1e-10;
const int N = 110;
int n;
int dcmp(double x, double y)
{
if (fabs(x - y) <= eps) return 0;
if (x > y) return 1;
return -1;
}
int sign(double x)
{
if (fabs(x) < eps) return 0;
if (x > 0) return 1;
return -1;
}
struct Point
{
double x, y;
Point(double x = 0, double y = 0) :x(x), y(y) { }
Point operator+ (Point t)
{
return Point(x + t.x, y + t.y);
}
Point operator- (Point t)
{
return Point(x - t.x, y - t.y);
}
Point operator* (double t)
{
return Point(x * t, y * t);
}
Point operator/ (double t)
{
return Point(x / t, y / t);
}
}p[N];
typedef Point Vector;
struct Line
{
Point p;
Vector v;
Line(Point p, Vector v) :p(p), v(v) {}
};
struct Segment
{
Point p1, p2;
};
double dot(Vector a, Vector b)
{
return a.x * b.x + a.y * b.y;
}
double cross(Vector a, Vector b)
{
return a.x * b.y - a.y * b.x;
}
double cross(Point A, Point B, Point C)
{
return cross(B - A, C - A);
}
double polygon_area(Point* p, int n)
{
double area = 0;
for (int i = 0; i < n; i++)
area += cross(p[i], p[(i + 1) % n]);
return area / 2.0;
}
Point get_segment_cross(Segment s, Line l) // 直线与线段的交点坐标
{
Vector w = s.p1 - s.p2;
Vector u = s.p1 - l.p;
double t = -cross(w, u) / cross(l.v, w);
return l.p + l.v * t;
}
int q;
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
cin >> p[i].x >> p[i].y;
cin >> q;
while (q--)
{
Point A, B;
cin >> A.x >> A.y >> B.x >> B.y;
Point tmp[N];
Vector v = B - A;
int cnt = 0;
for (int i = 0; i < n; i++)
{
if (cross(A, B, p[i]) >= 0) tmp[cnt++] = p[i]; //点再有向直线的左边,纳入新的点集
if (sign(cross(A, B, p[i])) * sign(cross(A, B, p[(i + 1) % n])) == -1)
tmp[cnt++] = get_segment_cross(Segment{ p[i], p[(i + 1) % n] }, Line{ A, v });//求交点,把交点加入点集
}
double ans = polygon_area(tmp, cnt);
printf("%.8lf\n", fabs(ans));
}
return 0;
}
原文地址:https://blog.csdn.net/zeisenphael/article/details/140620542
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
