C++ 笛卡尔树

一、性质

1. 堆性质： 笛卡尔树是一种满足堆性质的树。每个节点包含两个值：键值（key）和优先级值（priority）。在笛卡尔树中，根节点的优先级值最大，且每个节点的优先级值大于其子节点的优先级值。

2. 中序遍历： 笛卡尔树的中序遍历结果与原始数组的顺序一致。这意味着，如果你将笛卡尔树按中序遍历的顺序输出，就会得到原始数组的顺序。

3. 唯一性： 对于给定的键值数组，存在唯一的笛卡尔树与之对应。

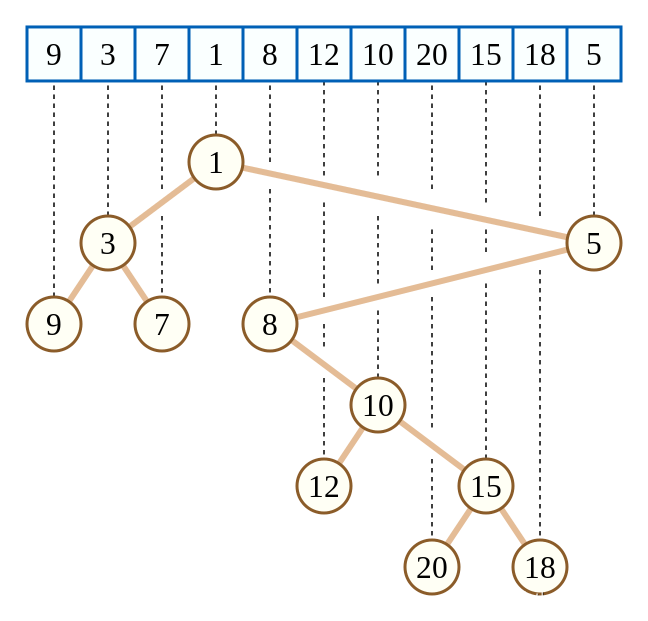（备注：图源于 维基百科）

二、构建笛卡尔树

1. 笛卡尔树通常是通过一个数组构建的，数组中的元素按照顺序表示树中节点的键值，另一个数组表示节点的优先级值。
2. 通过递归的方式构建笛卡尔树：在给定数组范围内，找到优先级值最大的元素作为根节点，然后递归构建左子树和右子树。

三、应用

1. 最小公共祖先（LCA）： 通过构建笛卡尔树，可以在O(1)时间内找到任意两个节点的最小公共祖先。

2. 区间最小值/最大值查询： 通过构建笛卡尔树，可以在O(log n)时间内查询给定区间的最小值或最大值。

四、源码

#include <iostream>
#include <vector>

using namespace std;

struct Node {
    int key;
    int priority;
    Node* left;
    Node* right;

    Node(int k, int p) : key(k), priority(p), left(nullptr), right(nullptr) {}
};

Node* buildCartesianTree(vector<int>& arr, vector<int>& priority, int start, int end) {
    if (start > end) {
        return nullptr;
    }

    int maxIndex = start;
    for (int i = start + 1; i <= end; i++) {
        if (priority[i] > priority[maxIndex]) {
            maxIndex = i;
        }
    }

    Node* root = new Node(arr[maxIndex], priority[maxIndex]);
    root->left = buildCartesianTree(arr, priority, start, maxIndex - 1);
    root->right = buildCartesianTree(arr, priority, maxIndex + 1, end);

    return root;
}

void inOrderTraversal(Node* root) {
    if (root) {
        inOrderTraversal(root->left);
        cout << "(" << root->key << ", " << root->priority << ") ";
        inOrderTraversal(root->right);
    }
}

int main() {
    vector<int> arr = { 9,3,7,1,8,12,10,20,15,18,5 };
    vector<int> priority = { 8,10,8,11,8,4,5,2,4,2,10 };

    Node* root = buildCartesianTree(arr, priority, 0, arr.size() - 1);

    cout << "Inorder traversal of Cartesian Tree: ";
    inOrderTraversal(root);
    cout << endl;

    return 0;
}

原文地址：https://blog.csdn.net/Doctor__Chen/article/details/136791742

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！