Java 集合框架:Java 中的优先级队列 PriorityQueue 的实现
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 018 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进一步完善自己对整个 Java 技术体系来充实自己的技术栈的同学。与此同时,本专栏的所有文章,也都会准备充足的代码示例和完善的知识点梳理,因此也十分适合零基础的小白和要准备工作面试的同学学习。当然,我也会在必要的时候进行相关技术深度的技术解读,相信即使是拥有多年 Java 开发经验的从业者和大佬们也会有所收获并找到乐趣。
–
在许多应用程序中,数据的优先级排序对于实现高效的数据处理和任务调度至关重要。Java 中的
PriorityQueue是一种基于堆的数据结构,广泛用于需要优先级排序的场景。与传统的队列不同,优先级队列可以确保在队列中的元素按照其优先级顺序进行处理,而不是按照插入顺序。本文将深入探讨PriorityQueue的实现,包括其基本概念、底层数据结构、各种操作的实现细节,并展示一些实际应用场景和简单用例,帮助你更好地理解和使用这一强大的数据结构。
文章目录
1、PriorityQueue 概述
1.1、优先级队列 介绍
PriorityQueue 在 Java 中是一种基于堆(Heap)数据结构实现的优先级队列。堆是一种特殊的完全二叉树,分为最小堆和最大堆。
- 在最小堆中,每个节点的值都小于或等于其子节点的值;
- 在最大堆中,每个节点的值都大于或等于其子节点的值。
Java 的 PriorityQueue 使用最小堆实现,因此队列头部总是优先级最高(值最小)的元素。
1.2、堆排序与最小堆
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆,是完全二叉树(树的所有级别都被完全填充,除了最低级别的节点从尽可能左侧填充之外)。
大根堆的要求是每个节点的值都不大于其父节点的值,即 A[PARENT[i]] >= A[i]。在数组的非降序排序中,需要使用的就是大根堆,因为根据大根堆的要求可知,最大的值一定在堆顶。
最小堆是一棵完全二叉树,非叶子结点的值不大于左孩子和右孩子的值。
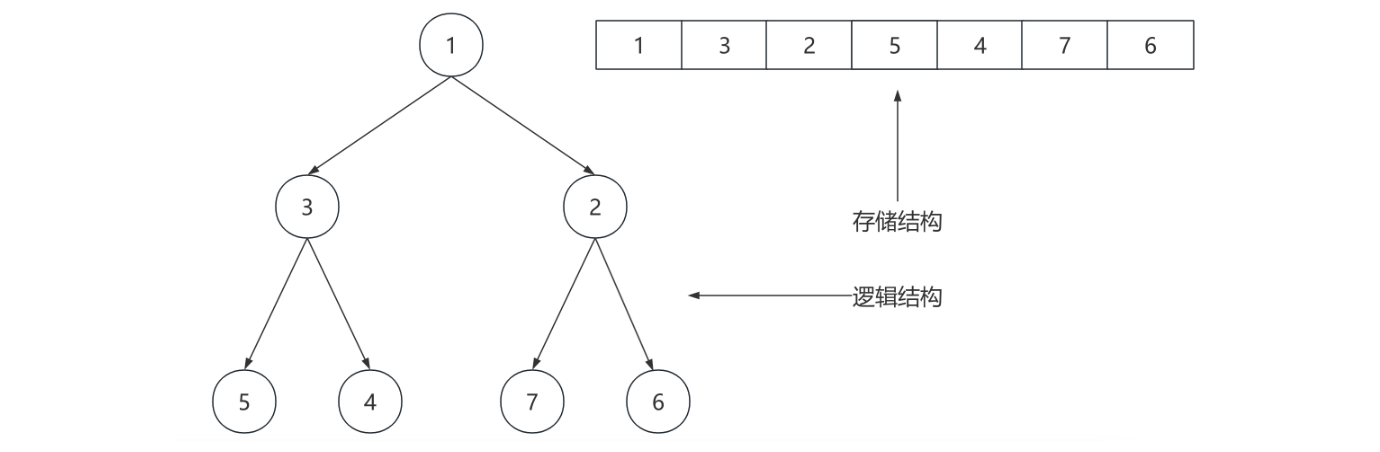
2、PriorityQueue 底层实现
2.1、PriorityQueue 数据结构
在 Java 中 PriorityQueue 用数组来表示堆,i 结点的父结点下标就为 (i – 1) / 2。它的左右子结点下标分别为 2 * i + 1 和 2 * i + 2。如第 0 个结点左右子结点下标分别为 1 和2。
public class PriorityQueue<E> extends AbstractQueue<E> implements java.io.Serializable {
// 省略其他方法和实现细节
...
// 默认初始容量为 11
private static final int DEFAULT_INITIAL_CAPACITY = 11;
/**
* 优先级队列,使用平衡二叉堆表示:
* queue[n] 的两个子节点为 queue[2*n+1] 和 queue[2*(n+1)]。
* 优先级队列按 comparator 排序,若 comparator 为 null,则按元素的自然顺序排序:
* 对堆中每个节点 n 及其每个后代 d,n <= d。最小值元素位于 queue[0]。
*/
transient Object[] queue; // 非私有以简化嵌套类访问
/**
* 优先级队列中的元素数量
*/
private int size = 0;
/**
* 比较器,若为 null 则使用元素的自然顺序
*/
private final Comparator<? super E> comparator;
/**
* 优先级队列被结构性修改的次数。详见 AbstractList。
*/
transient int modCount = 0; // 非私有以简化嵌套类访问
/**
* 创建默认初始容量为 11,按自然顺序排序的优先级队列。
*/
public PriorityQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
/**
* 创建指定初始容量,按自然顺序排序的优先级队列。
*
* @param initialCapacity 优先级队列的初始容量
* @throws IllegalArgumentException 若 initialCapacity 小于 1
*/
public PriorityQueue(int initialCapacity) {
this(initialCapacity, null);
}
/**
* 创建默认初始容量,按指定比较器排序的优先级队列。
*
* @param comparator 用于排序的比较器。若为 null,则使用元素的自然顺序。
* @since 1.8
*/
public PriorityQueue(Comparator<? super E> comparator) {
this(DEFAULT_INITIAL_CAPACITY, comparator);
}
/**
* 创建指定初始容量,按指定比较器排序的优先级队列。
*
* @param initialCapacity 优先级队列的初始容量
* @param comparator 用于排序的比较器。若为 null,则使用元素的自然顺序。
* @throws IllegalArgumentException 若 initialCapacity 小于 1
*/
public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) {
if (initialCapacity < 1) // 如果初始容量小于1则抛出异常
throw new IllegalArgumentException();
this.queue = new Object[initialCapacity]; // 初始化队列数组
this.comparator = comparator; // 设置比较器
}
/**
* 创建包含指定集合元素的优先级队列。
* 若指定集合是 SortedSet 或其他 PriorityQueue 实例,则优先级队列按相同顺序排序。
* 否则,按元素的自然顺序排序。
*
* @param c 要放入此优先级队列的集合
* @throws ClassCastException 若集合元素不能根据优先级队列的排序规则相互比较
* @throws NullPointerException 若集合或其中的任何元素为 null
*/
@SuppressWarnings("unchecked")
public PriorityQueue(Collection<? extends E> c) {
if (c instanceof SortedSet<?>) {
SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
this.comparator = (Comparator<? super E>) ss.comparator();
initElementsFromCollection(ss); // 从集合中初始化元素
} else if (c instanceof PriorityQueue<?>) {
PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c;
this.comparator = (Comparator<? super E>) pq.comparator();
initFromPriorityQueue(pq); // 从优先级队列中初始化
} else {
this.comparator = null;
initFromCollection(c); // 从一般集合中初始化
}
}
/**
* 创建包含指定优先级队列元素的优先级队列。按相同顺序排序。
*
* @param c 要放入此优先级队列的优先级队列
* @throws ClassCastException 若元素不能根据 c 的排序规则相互比较
* @throws NullPointerException 若优先级队列或其任何元素为 null
*/
@SuppressWarnings("unchecked")
public PriorityQueue(PriorityQueue<? extends E> c) {
this.comparator = (Comparator<? super E>) c.comparator();
initFromPriorityQueue(c); // 从优先级队列中初始化
}
/**
* 创建包含指定排序集元素的优先级队列。按相同顺序排序。
*
* @param c 要放入此优先级队列的排序集
* @throws ClassCastException 若排序集元素不能根据排序集的排序规则相互比较
* @throws NullPointerException 若排序集或其任何元素为 null
*/
@SuppressWarnings("unchecked")
public PriorityQueue(SortedSet<? extends E> c) {
this.comparator = (Comparator<? super E>) c.comparator();
initElementsFromCollection(c); // 从排序集中初始化元素
}
// 省略其他方法和实现细节
...
}
从这部分源码可以看出 PriorityQueue 使用数组实现一个平衡二叉堆,并提供了多种构造方法以便根据不同的需求初始化优先级队列
2.2、插入操作
插入操作(add 或 offer):插入新元素时,PriorityQueue 会将其添加到数组的末尾,然后进行上浮(percolate up)操作以维护堆的有序性:
- 将新元素添加到堆的末尾。
- 比较新元素与其父节点的值,如果新元素的值小于父节点的值,则交换它们的位置。
- 重复步骤 2,直到新元素到达合适的位置,满足堆的性质。
public class PriorityQueue<E> extends AbstractQueue<E> implements java.io.Serializable {
// 省略其他方法和实现细节
...
/**
* 将指定元素插入到优先级队列中。
*
* @return {@code true} (如 {@link Collection#add} 所指定)
* @throws ClassCastException 如果指定元素无法根据优先级队列的排序规则与当前队列中的元素进行比较
* @throws NullPointerException 如果指定元素为 null
*/
public boolean add(E e) {
return offer(e); // 调用 offer 方法插入元素
}
/**
* 将指定元素插入到优先级队列中。
*
* @return {@code true} (如 {@link Queue#offer} 所指定)
* @throws ClassCastException 如果指定元素无法根据优先级队列的排序规则与当前队列中的元素进行比较
* @throws NullPointerException 如果指定元素为 null
*/
public boolean offer(E e) {
if (e == null)
throw new NullPointerException(); // 若元素为 null,抛出空指针异常
modCount++; // 修改次数增加
int i = size; // 当前队列大小
if (i >= queue.length)
grow(i + 1); // 若当前大小已达数组容量上限,扩展数组容量
size = i + 1; // 队列大小增加
if (i == 0)
queue[0] = e; // 若队列为空,直接将元素放在根节点
else
siftUp(i, e); // 否则执行上滤操作,将元素放入适当位置
return true;
}
/**
* 上滤操作,将元素插入到适当的位置。
*
* @param k 要插入的位置索引
* @param x 要插入的元素
*/
private void siftUp(int k, E x) {
if (comparator != null)
siftUpUsingComparator(k, x); // 使用比较器进行上滤
else
siftUpComparable(k, x); // 使用自然排序进行上滤
}
/**
* 使用自然排序进行上滤操作。
*
* @param k 要插入的位置索引
* @param x 要插入的元素
*/
@SuppressWarnings("unchecked")
private void siftUpComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x; // 将元素转换为 Comparable
while (k > 0) {
int parent = (k - 1) >>> 1; // 计算父节点索引
Object e = queue[parent]; // 获取父节点元素
if (key.compareTo((E) e) >= 0)
break; // 如果插入元素大于等于父节点元素,则终止上滤
queue[k] = e; // 将父节点元素移到当前位置
k = parent; // 更新当前位置为父节点位置
}
queue[k] = key; // 将插入元素放到最终位置
}
/**
* 使用比较器进行上滤操作。
*
* @param k 要插入的位置索引
* @param x 要插入的元素
*/
@SuppressWarnings("unchecked")
private void siftUpUsingComparator(int k, E x) {
while (k > 0) {
int parent = (k - 1) >>> 1; // 计算父节点索引
Object e = queue[parent]; // 获取父节点元素
if (comparator.compare(x, (E) e) >= 0)
break; // 如果插入元素大于等于父节点元素,则终止上滤
queue[k] = e; // 将父节点元素移到当前位置
k = parent; // 更新当前位置为父节点位置
}
queue[k] = x; // 将插入元素放到最终位置
}
/**
* 扩展优先级队列的容量,确保其至少能够容纳指定的最小容量。
*
* @param minCapacity 所需的最小容量
*/
private void grow(int minCapacity) {
int oldCapacity = queue.length; // 旧的容量
// 若旧容量小于 64,则新容量为旧容量的两倍加上 2;否则,新容量增加 50%
int newCapacity = oldCapacity + ((oldCapacity < 64) ?
(oldCapacity + 2) :
(oldCapacity >> 1));
// 防止溢出的代码
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity); // 若新容量超出最大数组大小,则计算巨大容量
queue = Arrays.copyOf(queue, newCapacity); // 复制数组并扩展容量
}
/**
* 计算巨大的容量大小。
*
* @param minCapacity 所需的最小容量
* @return 合适的巨大容量大小
*/
private static int hugeCapacity(int minCapacity) {
if (minCapacity < 0) // 溢出检查
throw new OutOfMemoryError(); // 如果最小容量为负数,则抛出内存不足错误
return (minCapacity > MAX_ARRAY_SIZE) ?
Integer.MAX_VALUE : // 若最小容量超过最大数组大小,则返回 Integer 的最大值
MAX_ARRAY_SIZE; // 否则,返回最大数组大小
}
// 省略其他方法和实现细节
...
}
其中:
PriorityQueue中的add方法实际上调用offer方法将指定元素插入到优先级队列中。offer方法首先检查元素是否为null,然后增加modCount以记录修改次数。如果当前队列大小已达到数组容量上限,则调用grow方法扩展数组容量。之后,增加队列大小,并根据当前队列是否为空决定将元素放在根节点还是调用siftUp方法将元素插入到适当位置;PriorityQueue中的grow方法用于扩展队列的容量,当队列容量不足以容纳新元素时,会根据当前容量进行扩展。扩展规则是:如果当前容量小于 64,则新容量为旧容量的两倍加二;否则,新容量为旧容量的 1.5 倍。如果计算出的新容量超过了最大数组大小MAX_ARRAY_SIZE,则调用hugeCapacity方法来处理,确保不会溢出,并返回合适的新容量。在hugeCapacity方法中,如果所需容量大于最大数组大小MAX_ARRAY_SIZE,则返回Integer.MAX_VALUE,否则返回MAX_ARRAY_SIZE;PriorityQueue中的siftUp方法用于在插入元素时维护堆的有序性。该方法根据是否存在比较器comparator,调用不同的上滤操作:siftUpComparable使用元素的自然排序,siftUpUsingComparator使用提供的比较器。上滤过程中,通过不断比较新插入元素与其父节点元素,决定是否交换位置,直到找到合适的位置,以保证最小堆性质。
2.3、删除操作
删除堆顶元素时,PriorityQueue 会将堆尾元素移动到堆顶,然后进行下沉(percolate down)操作以维护堆的有序性:
- 将堆尾元素移动到堆顶,删除原堆顶元素。
- 比较新堆顶元素与其子节点的值,将其与值较小的子节点交换位置。
- 重复步骤 2,直到新堆顶元素到达合适的位置,满足堆的性质。
public class PriorityQueue<E> extends AbstractQueue<E> implements java.io.Serializable {
// 省略其他方法和实现细节
...
// 从优先级队列中移除并返回堆顶元素
@SuppressWarnings("unchecked")
public E poll() {
if (size == 0)
return null; // 如果队列为空,返回 null
int s = --size; // 获取当前队列的最后一个元素的位置,并将大小减1
modCount++; // 记录结构修改次数
E result = (E) queue[0]; // 记录并返回堆顶元素
E x = (E) queue[s]; // 取出新的堆尾元素(将要移动到堆顶的位置)
queue[s] = null; // 清空堆尾位置
if (s != 0)
siftDown(0, x); // 将堆尾元素下滤到正确的位置
return result; // 返回移除的堆顶元素
}
// 从队列中移除指定元素
/**
* 从队列中移除单个指定的元素(如果存在)。具体地说,
* 移除元素 {@code e},如果队列中存在一个或多个这样的元素。
* 如果队列因该操作而发生变化,则返回 {@code true}。
*
* @param o 要从队列中移除的元素
* @return 如果队列因该操作而发生变化,则返回 {@code true}
*/
public boolean remove(Object o) {
int i = indexOf(o); // 查找元素在队列中的位置
if (i == -1)
return false; // 如果元素不存在,则返回 false
else {
removeAt(i); // 移除元素并维持堆的性质
return true; // 返回 true,表示队列发生了变化
}
}
// 查找指定元素在队列中的位置
private int indexOf(Object o) {
if (o != null) {
for (int i = 0; i < size; i++)
if (o.equals(queue[i]))
return i; // 找到元素,返回其位置
}
return -1; // 元素不存在,返回 -1
}
// 移除队列中指定位置的元素
/**
* 移除队列中第 i 个元素。
* 该方法会保持堆的结构,并且可能会对元素进行交换。
* 返回值用于维护迭代器的正确性。
*
* @param i 要移除的元素的位置
* @return 被移除的元素(如果元素在最后一个位置被移除,则返回 null)
*/
@SuppressWarnings("unchecked")
private E removeAt(int i) {
// assert i >= 0 && i < size;
modCount++; // 记录结构修改次数
int s = --size; // 更新队列大小
if (s == i) // 如果移除的是最后一个元素
queue[i] = null; // 直接清空该位置
else {
E moved = (E) queue[s]; // 取出最后一个元素(将用来填补移除元素的位置)
queue[s] = null; // 清空原位置
siftDown(i, moved); // 下滤元素以维持堆性质
if (queue[i] == moved) { // 如果下滤操作未改变元素位置
siftUp(i, moved); // 上滤元素以维持堆性质
if (queue[i] != moved)
return moved; // 返回已移动的元素
}
}
return null; // 如果没有元素被移动,则返回 null
}
// 将元素 x 插入到位置 k,并维持堆的结构
private void siftDown(int k, E x) {
if (comparator != null)
siftDownUsingComparator(k, x); // 使用比较器进行下滤
else
siftDownComparable(k, x); // 使用元素的自然顺序进行下滤
}
// 使用自然顺序下滤元素
@SuppressWarnings("unchecked")
private void siftDownComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>)x; // 转换元素为 Comparable
int half = size >>> 1; // 计算非叶子节点的数量
while (k < half) { // 遍历非叶子节点
int child = (k << 1) + 1; // 假设左子节点最小
Object c = queue[child];
int right = child + 1;
// 如果右子节点存在且小于左子节点
if (right < size &&
((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
c = queue[child = right]; // 选择右子节点
// 如果当前元素不小于子节点
if (key.compareTo((E) c) <= 0)
break; // 下滤结束
queue[k] = c; // 交换当前元素与子节点
k = child; // 更新当前元素的位置
}
queue[k] = key; // 将元素放入正确的位置
}
// 使用比较器下滤元素
@SuppressWarnings("unchecked")
private void siftDownUsingComparator(int k, E x) {
int half = size >>> 1; // 计算非叶子节点的数量
while (k < half) { // 遍历非叶子节点
int child = (k << 1) + 1; // 假设左子节点最小
Object c = queue[child];
int right = child + 1;
// 如果右子节点存在且小于左子节点
if (right < size &&
comparator.compare((E) c, (E) queue[right]) > 0)
c = queue[child = right]; // 选择右子节点
// 如果当前元素不小于子节点
if (comparator.compare(x, (E) c) <= 0)
break; // 下滤结束
queue[k] = c; // 交换当前元素与子节点
k = child; // 更新当前元素的位置
}
queue[k] = x; // 将元素放入正确的位置
}
// 省略其他方法和实现细节
...
}
其中:
poll()方法: 从堆中移除并返回堆顶元素。将堆尾元素移到堆顶位置,然后通过下滤操作恢复堆的结构;remove(Object o)方法: 从队列中移除指定的元素。如果元素存在,则移除并维护堆的性质;如果元素不存在,则返回false;indexOf(Object o)方法: 查找指定元素在队列中的位置。如果找到,返回元素的位置;否则返回 `-1;removeAt(int i)方法: 移除队列中指定位置的元素。将队列最后一个元素移到移除位置,然后通过下滤和上滤操作维持堆的结构;siftDown(int k, E x)方法: 将元素x从位置k下滤到正确的位置,以保持堆的性质。根据是否使用比较器选择不同的下滤方法;siftDownComparable(int k, E x)方法: 使用元素的自然顺序下滤元素x;siftDownUsingComparator(int k, E x)方法: 使用比较器下滤元素x。
2.4、搜索操作
搜索性能:二叉排序树是为了实现动态查找而涉及的数据结构,它是面向查找操作的,在二叉排序树中查找一个节点的平均时间复杂度是 O(logn);在堆中搜索并不是第一优先级,堆是为了实现排序而实现的一种数据结构,它不是面向查找操作的,因为在堆中查找一个节点需要进行遍历,其平均时间复杂度是 O(n)。
/**
* 检查优先队列中是否包含指定的元素。
*
* @param o 要检查的元素
* @return 如果优先队列中包含指定的元素,则返回 {@code true};否则返回 {@code false}
*/
public boolean contains(Object o) {
// 通过调用 indexOf 方法查找元素的位置,如果 indexOf 返回 -1,说明元素不存在
return indexOf(o) != -1;
}
/**
* 查找指定元素在优先队列中的索引位置。
* 如果元素存在,返回其在队列中的位置;否则返回 -1。
*
* @param o 要查找的元素
* @return 如果元素存在,返回其在队列中的索引位置;否则返回 -1
*/
private int indexOf(Object o) {
// 如果待查找的元素不为 null
if (o != null) {
// 遍历队列中的所有元素
for (int i = 0; i < size; i++)
// 如果找到元素,返回其索引位置
if (o.equals(queue[i]))
return i;
}
// 如果元素未找到或元素为 null,返回 -1
return -1;
}
3、PriorityQueue 的使用
3.1、PriorityQueue 的使用场景
PriorityQueue 的使用场景包括任务调度、数据排序、任务优先级管理、数据压缩、图搜索算法、操作系统调度、网络数据包处理、事件驱动系统等。
- 任务调度:PriorityQueue 可以用于实现任务调度,根据任务的优先级来确定执行顺序。这对于提高系统的稳定性和效率非常有帮助;
- 数据排序:PriorityQueue 也可以用于对数据进行排序,通过将需要排序的数据加入队列,然后按照数据的优先级顺序依次输出,从而提高程序的性能;
- 任务优先级管理:PriorityQueue 适用于管理具有优先级关系的任务,例如,可以将紧急的任务设置为高优先级,不紧急的任务设置为低优先级。通过将任务加入优先级队列,可以实现任务的优先级管理,提高系统的响应速;
- 数据压缩:在哈夫曼编码等压缩算法中,可以使用优先队列来实现频率统计和编码的过程;
- 图搜索算法:在最短路径算法(如 Dijkstra 算法、A* 算法)中,可以使用优先队列来存储待访问的节点,并根据节点的优先级进行遍历;
- 操作系统调度:在操作系统中,可以使用优先队列来实现进程调度,根据进程的优先级来确定执行顺序;
- 网络数据包处理:在路由器等网络设备中,可以使用优先队列来处理网络数据包,根据数据包的优先级来确定传输顺序;
- 事件驱动系统:在事件驱动系统中,可以使用优先队列来管理事件队列,根据事件的优先级来确定处理顺序;
这些场景展示了 PriorityQueue 在提高系统效率、优化资源分配、以及增强系统响应速度方面的广泛应用。
3.2、PriorityQueue 的简单用例
我们通过一个简单的例子看一下 PriorityQueue 的插入和推出时其底层数组结构的变化。
public static void main(String[] args) {
ArrayList<Integer> arrayList = new ArrayList<>();
arrayList.add(1);
arrayList.add(3);
arrayList.add(2);
arrayList.add(5);
arrayList.add(4);
arrayList.add(7);
PriorityQueue<Integer> queue = new PriorityQueue<>(arrayList);
queue.add(6);
System.out.println(Arrays.toString(Arrays.stream(queue.toArray()).toArray()));
while (!queue.isEmpty()){
System.out.println(queue.poll());
System.out.println(Arrays.toString(Arrays.stream(queue.toArray()).toArray()));
}
}
输出:
[1, 3, 2, 5, 4, 7, 6]
1
[2, 3, 6, 5, 4, 7]
2
[3, 4, 6, 5, 7]
3
[4, 5, 6, 7]
4
[5, 7, 6]
5
[6, 7]
6
[7]
7
[]
原文地址:https://blog.csdn.net/weixin_45187434/article/details/140590597
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
