【数据结构与算法 | 灵神题单 | 自底向上DFS篇】力扣508, 1026, 951

1. 力扣508：出现次数最多的子树元素和

1.1 题目：

给你一个二叉树的根结点 root ，请返回出现次数最多的子树元素和。如果有多个元素出现的次数相同，返回所有出现次数最多的子树元素和（不限顺序）。

一个结点的 「子树元素和」 定义为以该结点为根的二叉树上所有结点的元素之和（包括结点本身）。

示例 1：

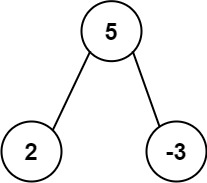
输入: root = [5,2,-3]
输出: [2,-3,4]

示例 2：

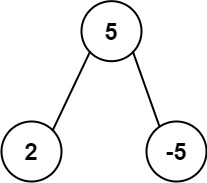
输入: root = [5,2,-5]
输出: [2]

提示:

• 节点数在 [1, 104] 范围内
• -105 <= Node.val <= 105

1.2 思路：

列表+哈希表+dfs递归

1.3 题解：

class Solution {
    // 列表用来存储所有出现次数最多的子树元素和
    List<Integer> list = new LinkedList<>();
    // 哈希表用来记录子树元素和出现的次数
    HashMap<Integer, Integer> map = new HashMap<>();
    // max用来记录子树元素和出现的最多次数
    int max;
    public int[] findFrequentTreeSum(TreeNode root) {
        // 节点数大于等于一个
        dfs(root);
        return toArr(list);

    }
    private int dfs(TreeNode node) {
        if(node == null) return 0;
        // 由定义：子树元素和等于该二叉树的所有节点之和
        node.val += dfs(node.left) + dfs(node.right);
        // 在哈希表中更新出现的元素和
        if(!map.containsKey(node.val)){
            map.put(node.val, 1);
        }else{
            map.put(node.val, 1+map.get(node.val));
        }
        int k = map.get(node.val);
        // 将原来的max值记录下来
        int old_max = max;
        // 再更新最新的max
        max = Integer.max(max, k);
        // 如果该节点的值（元素和）和之前的最多元素和一样
        // 那么就可以加入到列表中
        // 如果该元素和并不跟之前的意昂，反而是和已经更新过的元素和一样
        // 那么说明出现的新的最多元素和，将之前的列表清空，将该元素和加入到列表
        if(old_max == k){
            list.add(node.val);
        }else if (max == k){
            list.clear();
            list.add(node.val);
        }
        
        return node.val;
    }
    // 将列表转化为数组的方法
    private int[] toArr(List<Integer> list) {
        int[] arr = new int[list.size()];
        for(int i = 0; i < list.size(); i++){
            arr[i] = list.get(i);
        }
        return arr;
    }
}

2. 力扣1026：节点与其祖先之间的最大差值

2.1 题目：

给定二叉树的根节点 root，找出存在于 不同 节点 A 和 B 之间的最大值 V，其中 V = |A.val - B.val|，且 A 是 B 的祖先。

（如果 A 的任何子节点之一为 B，或者 A 的任何子节点是 B 的祖先，那么我们认为 A 是 B 的祖先）

示例 1：

输入：root = [8,3,10,1,6,null,14,null,null,4,7,13]
输出：7
解释： 
我们有大量的节点与其祖先的差值，其中一些如下：
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
在所有可能的差值中，最大值 7 由 |8 - 1| = 7 得出。

示例 2：

输入：root = [1,null,2,null,0,3]
输出：3

提示：

• 树中的节点数在 2 到 5000 之间。
• 0 <= Node.val <= 105

2.2 思路：

比较简单，dfs自顶向下递归，用形参记录路径上的最大值和最小值。

2.3 题解：

class Solution {
    int diff;
    public int maxAncestorDiff(TreeNode root) {
        // 树节点大于等于2
        dfs(root, root.val, root.val);
        return diff;
    }
    // max和min记录遍历到该个节点前的路径的最大值和最小值
    private void dfs(TreeNode node, int max, int min) {
        if(node == null){
            return;
        }
        // 分别更新最大值和最小值
        if(node.val > max){
            max = node.val;
        }
        if(node.val < min){
            min = node.val;
        }
        int d = max - min;
        // 更新最大差值
        diff = Integer.max(d, diff);
        dfs(node.left, max, min);
        dfs(node.right, max, min);
    }
}

3. 力扣951：翻转等价二叉树

3.1 题目：

我们可以为二叉树 T 定义一个 翻转操作 ，如下所示：选择任意节点，然后交换它的左子树和右子树。

只要经过一定次数的翻转操作后，能使 X 等于 Y，我们就称二叉树 X 翻转 等价 于二叉树 Y。

这些树由根节点 root1 和 root2 给出。如果两个二叉树是否是翻转 等价 的函数，则返回 true ，否则返回 false 。

示例 1：

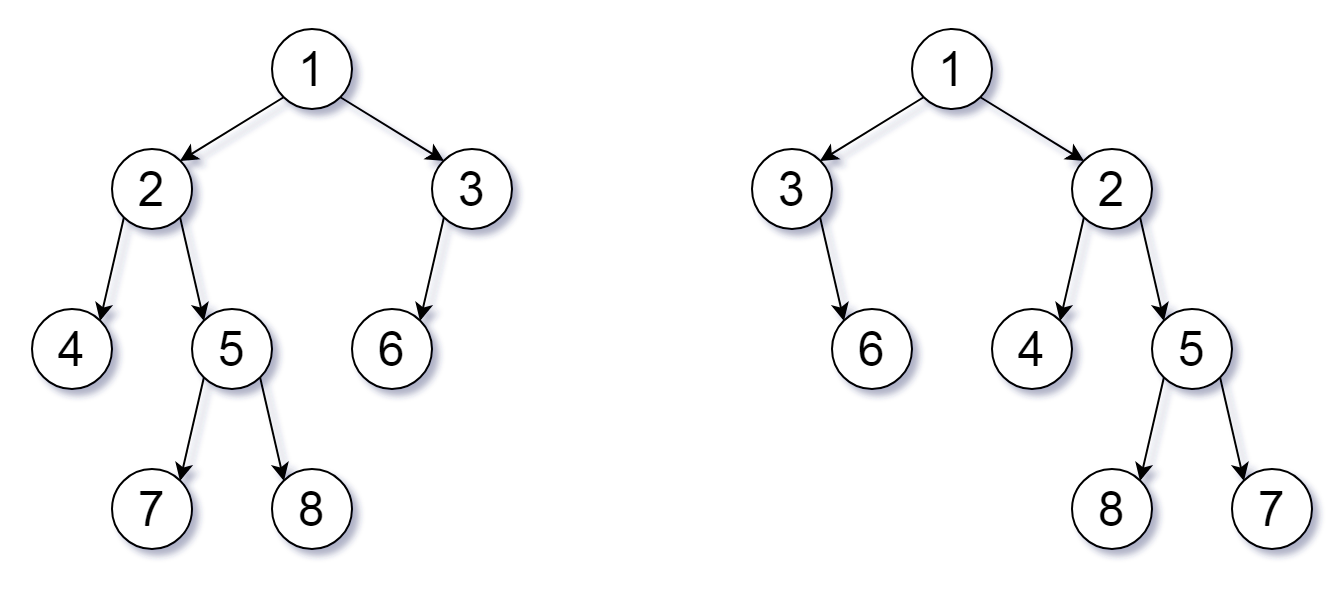
输入：root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
输出：true
解释：我们翻转值为 1，3 以及 5 的三个节点。

示例 2:

输入: root1 = [], root2 = []
输出: true

示例 3:

输入: root1 = [], root2 = [1]
输出: false

提示：

• 每棵树节点数在 [0, 100] 范围内
• 每棵树中的每个值都是唯一的、在 [0, 99] 范围内的整数

3.2 思路：

认真考虑到翻转的每种情况即可。

3.3 题解：

class Solution {
    public boolean flipEquiv(TreeNode root1, TreeNode root2) {
        if(root1 == null && root2 == null){
            return true;
        }else if (root1 == null && root2 != null || root1 != null && root2 == null){
            return false;
        }

        return dfs(root1, root2);

    }
    private boolean dfs(TreeNode node1, TreeNode node2) {
        if(node1 == null && node2 == null){
            return true;
        }else if (node1 != null && node2 == null || node1 == null && node2 != null){
             return false;
        }
        // 遍历到节点的值都不一样，肯定是不对的
        if(node1.val != node2.val){
            return false;
        }
        // 考虑翻转的四种情况
        // 前两种一组，后两种一组
        if(node1.left != null && node2.left != null && node1.left.val != node2.left.val){
            TreeNode p1 = node1.left;
            TreeNode p2 = node1.right;
            node1.left = p2;
            node1.right = p1;
        }else if (node1.right != null && node2.right != null && node1.right.val != node2.right.val){
            TreeNode p1 = node1.left;
            TreeNode p2 = node1.right;
            node1.left = p2;
            node1.right = p1;
        } else if (node1.left != null && node2.left == null){
            TreeNode p = node1.left;
            node1.left = null;
            node1.right = p;
        }else if (node1.right != null && node2.right == null){
            TreeNode p = node1.right;
            node1.right = null;
            node1.left = p;
        }

        
        return dfs(node1.left, node2.left) && dfs(node1.right, node2.right);
    }
}

原文地址：https://blog.csdn.net/2301_80912559/article/details/142335372

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！