数据结构与算法----复习Part 11 (哈希表)
本系列是算法通关手册LeeCode的学习笔记
算法通关手册(LeetCode) | 算法通关手册(LeetCode) (itcharge.cn)
目录
本系列为自用笔记,如有版权问题,请私聊我删除。
一,哈希表(HashTable)
也叫做散列表,根据关键码值 (Key Value)直接进行访问的数据结构。
哈希表通过【键 key】和【映射函数 Hash(key)】计算出相应的【值 value】,把关键码映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做【哈希函数】,存放记录的数组叫做【哈希表】
哈希表的关键思想时使用哈希函数,将键 key 映射到对应表的某个区块中。有以下两部分:
向哈希表中插入一个关键码值:哈希函数决定该关键字的对应值应该存放到表中的哪个区块,并将对应值存放到该区块中。
在哈希表中搜索一个关键码值:使用相同的哈希函数从哈希表中查找对应的区块,并在特定的区块搜索该关键字对应的值。

在上图例子中,使用 value = Hash(key) = key // 1000 作为哈希函数。
向哈希表中插入一个关键码值:通过哈希函数解析关键字,并将对应值存放到该区块中。
0138 通过哈希函数 Hash(key) = 0138 // 1000 = 0,得出应将 0138 分配到 0 所在的区
块中。
在哈希表中搜索一个关键码值:通过哈希函数解析关键字,并在特定的区块搜索该关键
字对应的值。
查找 2321,通过哈希函数,得出 2321 应该在 2 所对应的区块中,然后从 2 对应的区块
中继续搜索,并在 2 对应的区块中成功找到了 2321;
查找 3241,通过哈希函数,得出 3241 应该在 3 所对应的区块中,然后从 3 对应的区块
中继续搜索,没有找到对应值,则说明 3241 不在哈希表中。
二,哈希函数(Hash Function)
将哈希表中元素的关键值映射为元素存储位置的函数。
哈希函数是哈希表中最重要的部分,应满足:
1,哈希函数应易于计算,并且尽量使计算出来的索引值均匀分布;
2,哈希函数计算得到的哈希值是一个固定长度的输出值;
3,如果 Hash(key1) == Hash(key2) ,那么 key1、key2 可能相等也可能不相等。
2.1 直接定址法
取关键字本身 / 关键字的某个线性函数值作为哈希地址。
Hash(key) = key 或 Hask(key) = a * key + b
这种计算方式最简单且不会产生冲突。
2.2 除留余数法
假设哈希表的表长为 m,取一个不大于 m 但接近或等于 m 的质数 p,利用取模运算,将关键字转换为哈希地址。
Hash(key) = key mod p
其中 p 为不大于 m 的质数。
2.3 平方取中法
先通过求关键字平方值的方式扩大相近数之间的差别,然后根据表长取关键字平方值的中间几位数为哈希地址。
Hash(key) = (key * key) // 100 mod 1000
先计算平方,去除末尾 2 位数,再取中间 3 位数作为哈希地址。
这种方法因为关键字平方值的中间几位数和原关键字的每一位数都相关,所以产生的哈希地址也比较均匀,有利于减少冲突的发生。
2.4基数转换法
将关键字看成另一种进制的数,再转回原来进制的数,然后选其中几位作为哈希地址。
三,哈希冲突(Hash Collision)
不同关键字通过同一个哈希函数可以得到同一哈希地址:
key1 != key2
Hash(key1) == Hash(key2)
称为哈希冲突
常用解决哈希冲突的方法主要是两类:【开放地址法(Open Addressing)】和【链地址法(Chaining)】
3.1 开放地址法
指的是将哈希表中的【空地址】向处理冲突开放。当哈希表未满时,处理冲突时,需要尝试另外的单元,直到找到空的单元为止。
发生冲突时,开放地址法按照
H( i ) = ( Hash( key ) + F( i ) )mod m , i = 1, 2, 3...n ( n <= m - 1 )
的方法求得后继哈希地址。
H( i ) 是在处理冲突中得到的地址序列。即在第一个冲突 ( i = 1 )是经过处理得到了一个新地址
H( 1 ),如果在 H( 1 ) 处仍然冲突,经过处理得到 H( 2 ) ,直到求得的 H( n ) 不再冲突。
Hash( key ) 是哈希函数,m 是表长,对 m 取余保证得到的下一个地址一定落在哈希表中。
F( i ) 是冲突解决方法,取法有以下几种:
线性探测法: F( i ) = 1, 2, 3,,,, m - 1.
二次探测法:F( i ) = 1 ** 2, -1 ** 2, 2 ** 2, -2 ** 2,,,
伪随机数序列:F( i ) = 伪随机数序列
举个例子说说明一下如何用以上三种冲突解决方法处理冲突,并得到新地址 H(i)。例如,在长度为 11 的哈希表中已经填有关键字分别为 28、49、18 的记录
哈希函数为 Hash(key)=key mod 11。现在将插入关键字为 38 的新纪录。根据哈希函数得到的哈希地址为 55,产生冲突。接下来分别使用这三种冲突解决方法处理冲突。
- 使用线性探测法:得到下一个地址 H(1)=(5+1)mod 11=6,仍然冲突;继续求出 H(2)=(5+2)mod 11=7,仍然冲突;继续求出 H(3)=(5+3)mod 11=8,8 对应的地址为空,处理冲突过程结束,记录填入哈希表中序号为 8 的位置。
- 使用二次探测法:得到下一个地址 H(1)=(5+1×1)mod 11=6,仍然冲突;继续求出 H(2)=(5−1×1)mod 11=4,4 对应的地址为空,处理冲突过程结束,记录填入哈希表中序号为 4 的位置。
- 使用伪随机数序列:假设伪随机数为 9,则得到下一个地址H(1)=(9+5)mod 11=3,3 对应的地址为空,处理冲突过程结束,记录填入哈希表中序号为 3 的位置。
3.2 链地址法
将具有相同哈希地址的元素(或记录)存储在同一个线性链表中,是一种更加常用的哈希冲突解决方法。
假设哈希函数产生哈希地址的区间为 [ 0, m - 1 ],哈希表的表长为 m,则可以将哈希表定义为一个有 m 个头节点组成的链表指针数组 T
这样在插入关键字的时候,我们只需要通过哈希函数计算出对应的哈希地址,然后将其
以链表节点的形式插入到以 T[ i ] 为头节点的单链表中。如果每次插入的位置为表头,则插入
的时间复杂度为 O( 1 ).
而在查询关键字的时候,我们只需要通过哈希函数计算出对应的哈希地址 i,然后将对应
位置上的链表整个扫描一遍,比较链表中的每个链节点的键值与查询的键值是否一致。
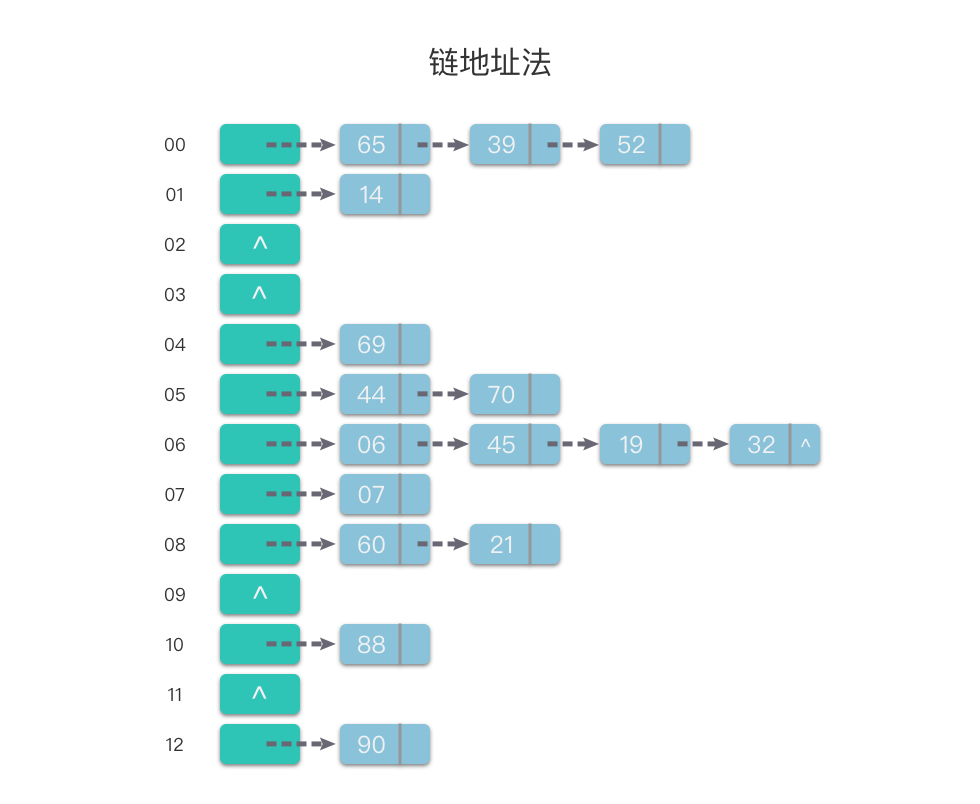
相对于开放地址法,采用链地址法处理冲突要多占用一些存储空间,但它可以减少在进行插入和查找具有相同哈希地址关键字的操作过程中的平均查找长度。
四,例题
class MyHashSet:
def __init__(self):
self.buckets = 1009
self.table = [[] for _ in range(self.buckets)]
def hash(self, key):
return key % self.buckets
def add(self, key: int) -> None:
hashkey = self.hash(key)
if key in self.table[hashkey]:
return
self.table[hashkey].append(key)
def remove(self, key: int) -> None:
hashkey = self.hash(key)
if key not in self.table[hashkey]:
return
self.table[hashkey].remove(key)
def contains(self, key: int) -> bool:
hashkey = self.hash(key)
return key in self.table[hashkey]class MyHashMap:
def __init__(self):
self.buckets = 1009
self.table = [[] for _ in range(self.buckets)]
def hash(self, key):
return key % self.buckets
def put(self, key: int, value: int) -> None:
hashkey = self.hash(key)
for item in self.table[hashkey]:
if item[0] == key:
item[1] = value
return
self.table[hashkey].append([key, value])
def get(self, key: int) -> int:
hashkey = self.hash(key)
for item in self.table[hashkey]:
if item[0] == key:
return item[1]
return -1
def remove(self, key: int) -> None:
hashkey = self.hash(key)
for i, item in enumerate(self.table[hashkey]):
if item[0] == key:
self.table[hashkey].pop(i)
return
设计哈希映射时,在遍历 table 中,使用 item 作为存储的元素
并以此判断 self.table[hashkey] 中是否有 key 为关键字的元素
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
res = dict()
for num in nums:
if num in res:
return True
res[num] = num
return Falseclass Solution:
def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:
res = dict()
for i, num in enumerate(nums):
if num in res:
if i - res[num] <= k:
return True
res[num] = i
return False
class Solution:
def areOccurrencesEqual(self, s: str) -> bool:
res = dict()
for i in s:
if i in res:
res[i] += 1
else:
res[i] = 1
flag = int(res[s[0]])
for item in res.values():
if item != flag:
return False
return True算法通关手册(LeetCode) | 算法通关手册(LeetCode)
原文内容在这里,如有侵权,请联系我删除。
原文地址:https://blog.csdn.net/m0_62608770/article/details/136354516
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!

