【机器学习笔记15】多分类混淆矩阵、F1-score指标详解与代码实现（含数据）

推荐阅读

参考文章

• 4.4.2分类模型评判指标（一） - 混淆矩阵(Confusion Matrix)_进击的橘子猫的博客-CSDN博客_混淆矩阵

前言

之前在逻辑回归的文章中简单提到过F1-score，但并没有详细对其进行说明和代码实现。这里补一下。

混淆矩阵简介

混淆矩阵（又称误差矩阵）是评判模型结果的指标，属于模型评估的一部分。混淆矩阵多用于判断分类器的优劣，适用于分类型数据模型。如分类树、逻辑回归、线性判别分析等方法。

除了混淆矩阵外，常见的分类型模型判别标准还有ROC曲线和AUC面积，本篇不对另外两种进行拓展。

二分类混淆矩阵

为了便于理解，我们从二分类混淆模型开始，引出四个基本指标（又称一级指标），并进一步引出其他指标。

一级指标

• TP(True Positive，真阳性)：样本的真实类别是正类，并且模型预测的结果也是正类。
• FP(False Positive，假阳性)：样本的真实类别是负类，但是模型将其预测成为正类。
• TN(True Negative，真阴性)：样本的真实类别是负类，并且模型将其预测成为负类。
• FN(False Negative，假阴性)：样本的真实类别是正类，但是模型将其预测成为负类。

二级指标

通过混淆矩阵统计出的一级指标，可以进一步衍生出以下二级指标。

准确率（Accuracy）

含义： 分类模型所有判断正确的结果占总观测值的比重。（准确率是针对整个模型）

公式：
$$Acc=\frac{TP+TN}{TP+TN+FP+FN}$$

注意别把准确率和精确率搞混了。

精确率（Precision）

含义：在模型预测为正类的所有结果中，模型预测正确的比重。

公式：
$$Pc=\frac{TP}{TP+FP}$$

召回率（Recall）

召回率又称灵敏度（Sensitivity）。

含义：在真实值为正类的所有结果中，模型预测正确的比重。

公式：
$$Rc=\frac{TP}{TP+FN}$$

特异度（Specificity）

含义：在真实值为负类的所有结果中，模型预测正确的比重。

公式：
$$Sc=\frac{TN}{TN+FP}$$

相对于前三个二级指标，特异度用的比较少。

三级指标（F-score）

通过二级指标可以引出三级指标F Score。

F-Score是可以综合考虑精确度（Precision）和召回率（Recall）的调和值，公式如下：
$$FScore=(1+{\beta }^2)\frac{Precision\times Recall}{{\beta }^{2}Precision+Recall}$$

• 当我们认为精确度更重要，调整$\beta <1$。
• 当我们认为召回率更重要，调整$\beta >1$。
• 当$\beta =1$时，精确度和召回率权重相同。此时称为F1-Score或F1-Measure。

F1-score

公式（即$\beta =1$）:
$$F1Score=\frac{2Precision\times Recall}{Precision+Recall}$$

多分类混淆矩阵

现在将二分类拓展至多分类混淆矩阵。为了便于理解，这里举一个具体的示例。

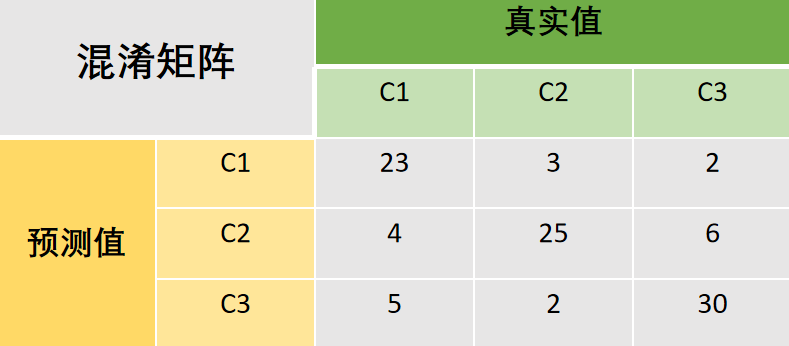
准确率（Accuracy）

准确率是对于整体而言的，指分类模型所有预测正确的结果占总观测值的比重。可以很容易看出，对于多分类混淆矩阵，所有预测正确的结果就是对角线之和。

于是这个示例的准确率为：
$$\begin{array}{rl}Acc& =\frac{23+25+30}{23+3+2+4+25+6+5+2+30}\\ & =\frac{78}{100}\\ & =0.78\end{array}$$

精确率（Precision）

精确率是对于单个类别而言。所以这里需要把$C1,C2,C3$的精确度都算出来。这里就只举例$C1$的精确度如何计算。

某类的精确率：在模型预测为本类的所有结果中，模型预测正确的比重。(分母为对行求和)

令$C1$的精确率为$P{c}_1$ ：
$$\begin{array}{rl}P{c}_1=& \frac{23}{23+3+2}\\ & =0.821\end{array}$$

召回率（Recall）

某类的召回率：在真实值为本类的所有结果中，模型预测正确的比重。（分母为对列求和）

令$C1$的召回率为$R{c}_1$ ：
$$\begin{array}{rl}R{c}_1=& \frac{23}{23+4+5}\\ & =0.719\end{array}$$

特异度（Specificity）

一般都用不着，不过这里还是算一遍吧。

要计算这个东西，需要把上面的图统计为二分类混淆矩阵的形式才好解释。

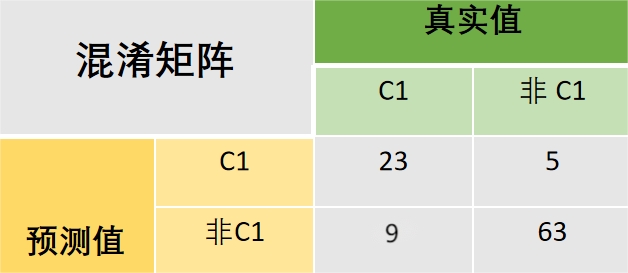
特异度：在真实值为负类的所有结果中，模型预测正确的比重。

令$C1$的特异度为$S{c}_1$ ：
$$\begin{array}{rl}S{c}_1& =\frac{TN}{TN+FP}\\ & =\frac{63}{5+63}\\ & =0.93\end{array}$$

F1-score

$$\begin{array}{rl}F1Scor{e}_1& =\frac{2P{c}_{1}R{c}_1}{P{c}_1+R{c}_1}\\ & =\frac{2\times 0.821\times 0.719}{0.821+0.719}\\ & =0.767\end{array}$$

示例与代码实现

前景题要：现在已经通过某种多分类器（例如softmax分类器）求出了测试集的预测结果。现在需要对预测结果进行评估。

• y_predict：样本集的预测结果，维度(1,N)。N代表参加测试的有N个样本。
• y_true：样本集的真实标签，维度(1,N)。

数据如下：

y_true is :    [0 1 3 2 3 0 2 2 3 3 3 0 1 4 4 0 1 3 2 2 1 3 2 0 2 4 1 0 1 0 4 3 3 3 2 1 0 3 0]
y_predict is : [0 1 3 0 2 0 2 2 1 2 3 0 0 4 4 0 1 4 2 2 0 3 2 1 2 4 3 1 1 3 4 3 0 2 2 3 2 2 1]

step1：统计混淆矩阵

def statistics_confusion(y_true,y_predict):
    """
     统计混淆矩阵
     
    :param y_true: 真实label 
    :param y_predict: 预测label
    :return: 
    """
    confusion = np.zeros((5, 5))
    for i in range(y_true.shape[0]):
        confusion[y_predict[i]][y_true[i]] += 1
    return confusion

输出:

step2：计算二级指标

准确率（Accuracy）

def cal_Acc(confusion):
    """
    计算准确率

    :param confusion: 混淆矩阵
    :return: Acc
    """
    return np.sum(confusion.diagonal())/np.sum(confusion)

输出：

Acc is 0.5641025641025641

精确率（Precision）

def cal_Pc(confusion):
    """
    计算每类精确率

    :param confusion: 混淆矩阵
    :return: Pc
    """
    return confusion.diagonal()/np.sum(confusion,axis=1)

输出：

Pc is [0.5        0.42857143 0.58333333 0.57142857 0.8       ]

每列对应一个类的精确率。

召回率（Recall）

def cal_Rc(confusion):
    """
    计算每类召回率

    :param confusion: 混淆矩阵
    :return: Rc
    """
    return confusion.diagonal()/np.sum(confusion,axis=0)

输出:

Rc is [0.44444444 0.42857143 0.875      0.36363636 1.        ]

每列对应一个类的召回率。

step3：计算F1-score

def cal_F1score(PC,RC):
    """
    计算F1 score

    :param PC: 精准率
    :param RC: 召回率
    :return: F1 score
    """
    return 2*np.multiply(PC,RC)/(PC+RC)

输出：

F1-score is [0.47058824 0.42857143 0.7        0.44444444 0.88888889]

每列对应一个类的F1 score。

为了让结果和代码更加美观，可以打一下包。

完整代码

import numpy as np

class Myreport:
    def __init__(self):
        self.__confusion = None

    def __statistics_confusion(self,y_true,y_predict):
        self.__confusion = np.zeros((5, 5))
        for i in range(y_true.shape[0]):
            self.__confusion[y_predict[i]][y_true[i]] += 1

    def __cal_Acc(self):
        return np.sum(self.__confusion.diagonal()) / np.sum(self.__confusion)

    def __cal_Pc(self):
        return self.__confusion.diagonal() / np.sum(self.__confusion, axis=1)

    def __cal_Rc(self):
        return self.__confusion.diagonal() / np.sum(self.__confusion, axis=0)

    def __cal_F1score(self,PC,RC):
        return 2 * np.multiply(PC, RC) / (PC + RC)

    def report(self,y_true,y_predict,classNames):
        self.__statistics_confusion(y_true,y_predict)
        Acc = self.__cal_Acc()
        Pc = self.__cal_Pc()
        Rc = self.__cal_Rc()
        F1score = self.__cal_F1score(Pc,Rc)
        str = "Class Name\t\tprecision\t\trecall\t\tf1-score\n"
        for i in range(len(classNames)):
           str += f"{classNames[i]}   \t\t\t{format(Pc[i],'.2f')}   \t\t\t{format(Rc[i],'.2f')}" \
                  f"   \t\t\t{format(F1score[i],'.2f')}\n"
        str += f"accuracy is {format(Acc,'.2f')}"
        return str

测试：

myreport = Myreport()
print(myreport.report(y_true = y_true,y_predict=y_predict,classNames=['C1','C2','C3','C4','C5']))

输出：

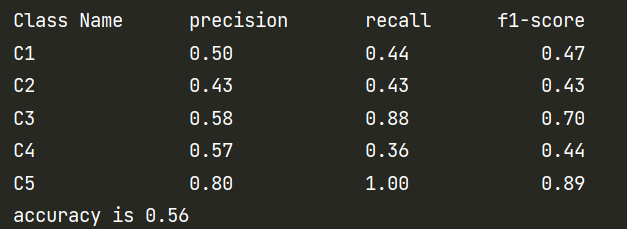
使用sklearn对比计算结果是否正确

from sklearn.metrics import classification_report # 结果评估
myreport = Myreport()
print("=====自己实现的结果=====")
print(myreport.report(y_true = y_true,y_test=y_predict,classNames=['C1','C2','C3','C4','C5']))
print("=====使用sklrean的结果=====")
print(classification_report(y_true, y_predict, target_names=['C1','C2','C3','C4','C5']))

结果对比

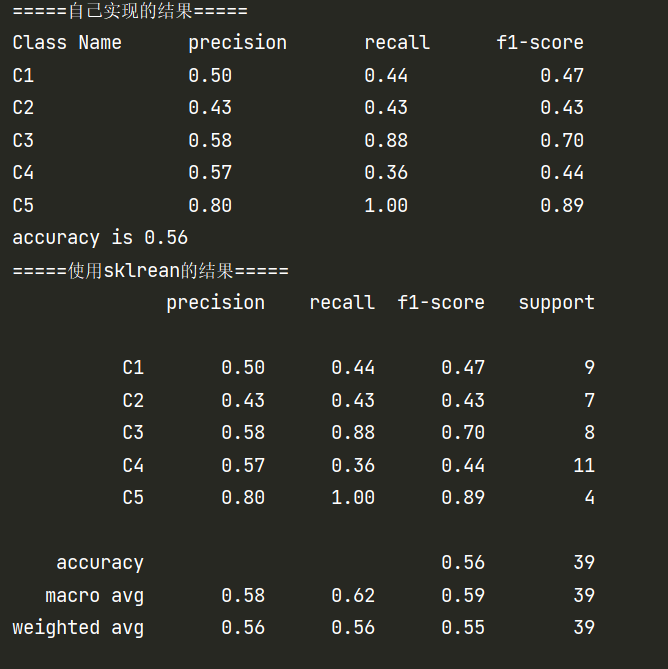
只能说一模一样。

原文地址：https://blog.csdn.net/qq_52466006/article/details/127633149

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！