【动手学强化学习】第四章 动态规划算法知识点总结

动态规划简介

• 动态规划的基本思想是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到目标问题的解
• 使用动态规划解决问题，该问题需要满足两个条件：最优子结构和子问题重叠
• 最优子结构（Optimal Substructure）: 这意味着问题的最优解包含了其子问题的最优解。换句话说，如果我们知道子问题的最优解，我们可以组合这些解来构建原问题的最优解。这允许我们通过自底向上的方式构建问题的解，从小子问题开始，逐步构建至整个问题的解
• 子问题重叠（Overlapping Subproblems）: 这意味着问题可以被分解为相互重叠的子问题。换句话说，不同的子问题可能包含相同的更小子问题。动态规划通过保存这些子问题的解（通常是在一个表格中），可以避免重复解决相同的子问题，从而提高效率。
• 动态规划会保存已解决的子问题的答案，在求解目标问题的过程中，需要这些子问题答案时就可以直接利用，避免重复计算
• 本章介绍如何用动态规划的思想来求解在马尔可夫决策过程中的最优策略

基于动态规划的强化学习算法

• 基于动态规划的强化学习算法主要有两种：一是策略迭代（policy iteration），二是价值迭代（value iteration）。其中，策略迭代由两部分组成：策略评估（policy evaluation）和策略提升（policy improvement）
• 策略迭代的两个步骤如下图所示：
  
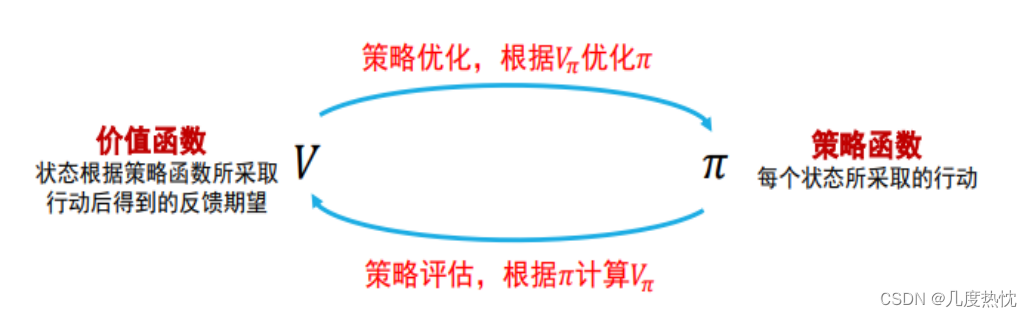
• 策略迭代中的策略评估使用贝尔曼期望方程来得到一个策略的状态价值函数，这是一个动态规划的过程
• 价值迭代直接使用贝尔曼最优方程来进行动态规划，得到最终的最优状态价值
• 基于动态规划的这两种强化学习算法要求事先知道环境的状态转移函数和奖励函数，也就是需要知道整个马尔可夫决策过程
• 在这样一个白盒环境中，不需要通过智能体和环境的大量交互来学习，可以直接用动态规划求解状态价值函数。但是，现实中的白盒环境很少，这也是动态规划算法的局限之处，我们无法将其运用到很多实际场景中
• 策略迭代和价值迭代通常只适用于有限马尔可夫决策过程，即状态空间和动作空间是离散且有限的

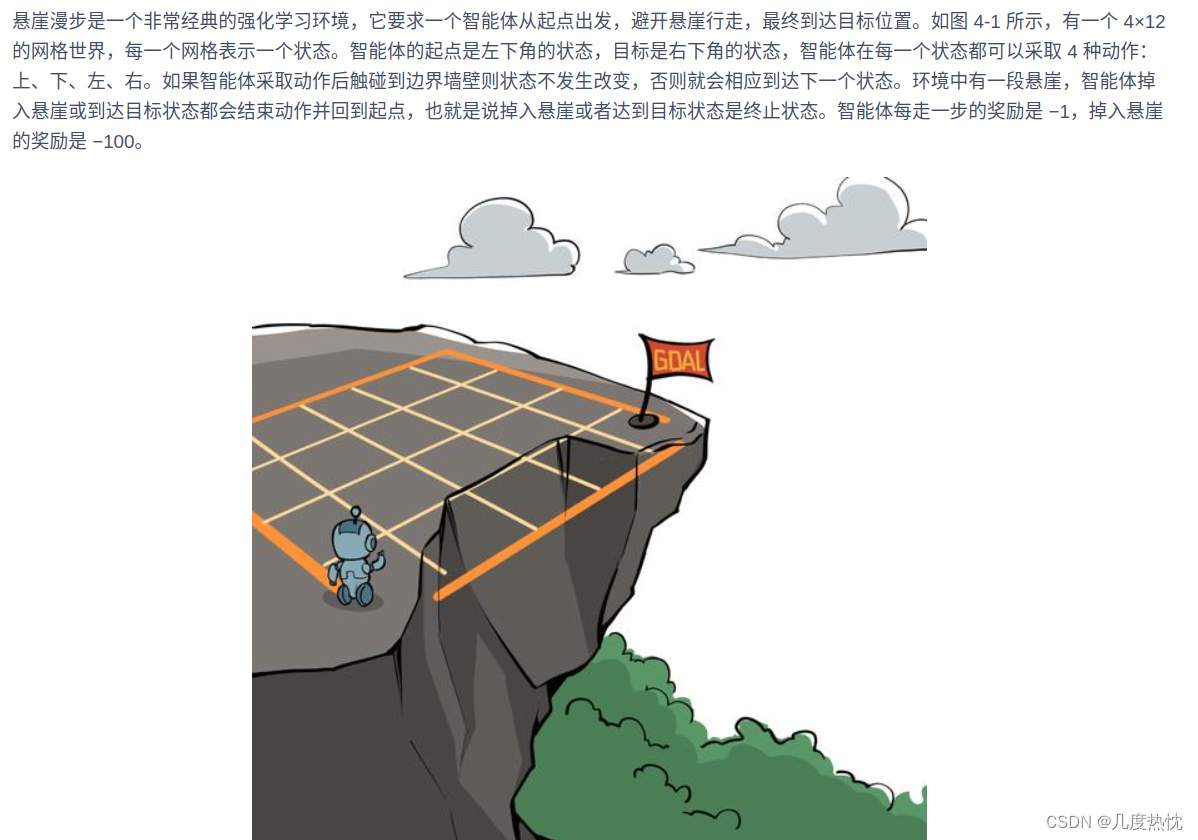
悬崖漫步环境

• 本节使用策略迭代和价值迭代来求解悬崖漫步（Cliff Walking）这个环境中的最优策略
• 除了在起始位置，当nrow=3的时候，就是在最外圈，agent处于悬崖或目标状态
  

策略迭代算法

• 策略迭代包含策略评估和策略提升两个步骤
• 策略迭代是策略评估和策略提升不断循环交替，直至最后得到最优策略的过程

---

策略评估：根据$\pi$计算$V^{\pi }$

• 策略评估这一过程用来计算一个策略的状态价值函数

• 回顾状态价值函数的贝尔曼期望方程：
  $$\begin{array}{rl}{V}^{\pi }(s)& =E_{\pi }[G_t|]S_t=s]\\ & =E_{\pi }[R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\dots |S_t=s]\\ & =E_{\pi }[R_t+\gamma (R_{t+1}+\gamma R_{t+2}+\dots )|S_t=s]\\ & =E_{\pi }[R_t+\gamma G_{t+1}|S_t=s]\\ & =E_{\pi }[R_t+\gamma V_{\pi }(S_{t+1})|S_t=s]]\\ & =\sum _{a_t\in A}\pi (a_t|s_t)[R(s_t,a_t)+\gamma \sum _{s_{t+1}\in S}P(s_{t+1}|s_t,a_t)V_{\pi }(s_{t+1})]\end{array}$$

• 在基于动态规划的强化学习中，已知奖励函数和状态转移函数时，我们可以根据下一个状态的价值来计算当前状态的价值

• 根据动态规划的思想，可以把计算下一个可能状态的价值当成一个子问题，把计算当前状态的价值看作当前问题。在得知子问题的解后，就可以求解当前问题

• 更一般的，考虑所有的状态，就变成了用上一轮的状态价值函数(子问题)来计算当前这一轮的状态价值函数(当前问题)
  $$\begin{array}{rl}{V}^{k+1}(s)& =\sum _{a_t\in A}\pi (a_t|s_t)[R(s_t,a_t)+\gamma \sum _{s_{t+1}\in S}P(s_{t+1}|s_t,a_t)V^k(s_{t+1})]\end{array}$$
  

策略提升：根据$V^{\pi }$优化$\pi$

• 使用策略评估计算得到当前策略的状态价值函数之后，我们可以据此来改进该策略

• 假设此时对于策略$\pi$，我们已经知道其价值$V^{\pi }$，也就是知道了在策略下从每一个状态$s$出发最终得到的期望回报

• 如何改变策略来获得在状态下更高的期望回报呢 ,假设智能体在状态$s$下采取动作$a$（个人理解，这里的动作$a$不一定是根据策略做出的），之后的动作依旧遵循策略$\pi$，根据状态价值函数和动作价值函数的关系，此时得到的期望回报其实就是动作价值$Q^{\pi }(s,a)$
  

• 若有$Q^{\pi }(s,a)>V^{\pi }(s)$,则表明在状态$s$下采取动作$a$（个人理解，这里的动作$a$不一定是根据策略做出的）会比原来的策略$\pi (a|s)$得到更高的期望回报

• 以上假设只是针对一个状态，现在假设存在一个确定性策略${\pi }^{\prime }$（在每个状态时只输出一个确定性的动作），在任意一个状态$s$下，都满足

$$\begin{array}{r}{Q}^{\pi }(s,{\pi }^{\prime }(s))\ge V^{\pi }\end{array}$$

• 根据状态价值函数和动作价值函数的关系,以及确定性策略 在任意状态下可得
  $$\begin{array}{r}{V}^{{\pi }^{\prime }}(s)\ge V^{\pi }(s)\end{array}$$

• 策略提升定理（policy improvement theorem）说明了如何通过已知的最优值函数来改进策略，进而达到最优策略

• 这个定理的核心在于指出，对于任何策略，都可以通过选择在每个状态下能够获得最大期望回报的动作来获得一个至少同样好（甚至更好）的策略

• 可以直接贪心地在每一个状态选择动作价值最大的动作
  π ′ ( s ) = a r g max ⁡ a Q π ( s , a ) = a r g max ⁡ a { r ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V π ( s ′ ) } \begin{aligned} \pi'(s) = arg\max_aQ^\pi(s,a) = arg \max_a \{ r(s,a) + \gamma \sum_{s'}P(s'|s,a)V^\pi(s') \} \end{aligned} π′(s)=argamax​Qπ(s,a)=argamax​{r(s,a)+γs′∑​P(s′∣s,a)Vπ(s′)}​

• 构造的贪心策略${\pi }^{\prime }$满足策略提升定理的条件，所以策略${\pi }^{\prime }$能够比策略$\pi$更好或者至少与其一样好。这个根据贪心法选取动作从而得到新的策略的过程称为策略提升。当策略提升之后得到的策略${\pi }^{\prime }$和之前的策略$\pi$一样时，说明策略迭代达到了收敛，此时和就是最优策略。

---

• 总结：策略评估是使用$\pi$得到$V^{\pi }$,通过贝尔曼期望方程（Bellman Expectation Equation）来迭代计算每个状态的值，得到一个值函数，它准确地估计了在当前策略下，从任何状态开始的期望回报；策略提升是根据$V^{\pi }$优化$\pi$，通过选择在每个状态下能够获得最大期望回报的动作来实现改进当前策略，根据策略评估得到的值函数，对于每个状态，选择使得期望回报最大化的动作，产生一个新的策略，它在每个状态下都执行最优动作；策略迭代算法通过交替执行策略评估和策略提升（策略优化）步骤来寻找最优策略。

策略提升定理的证明

• 通过以下推导过程可以证明，使用上述提升公式得到的新策略${\pi }^{\prime }$在每个状态的价值不低于原策略$\pi$在该状态的价值

• 假设在任意一个状态$s$下，都满足： $$\begin{array}{r}{Q}^{\pi }(s,{\pi }^{\prime }(s))\ge V^{\pi }\end{array}$$

• 证明：

  $$\begin{array}{rl}{V}^{\pi }(s)\le Q^{\pi }(s,{\pi }^{\prime }(s))& =E_{{\pi }^{\prime }}[R_t+\gamma V^{\pi }(S_{t+1})|S_t=s]\\ & \le E_{{\pi }^{\prime }}[R_t+\gamma Q^{\pi }(S_{t+1},{\pi }^{\prime }(S_{t+1}))|S_t=s]\\ & =E_{{\pi }^{\prime }}[R_t+\gamma R_{t+1}+{\gamma }^2{V}^{\pi }(S_{t+2})|S_t=s]\\ & \le E_{{\pi }^{\prime }}[R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{V}^{\pi }(S_{t+3})|S_t=s]\\ & ⋮\\ & \le E_{{\pi }^{\prime }}[R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{V}^{\pi }(S_{t+3})+\dots |S_t=s]\\ & =E_{{\pi }^{\prime }}[G_t|S_t=s]根据回报的定义推出的\\ & =V^{{\pi }^{\prime }}(s)\end{array}$$

• 推导过程中的每一个时间步都用到局部动作价值优势$V^{\pi }(S_{t+1})\le Q^{\pi }(S_{t+1},{\pi }^{\prime }(S_{t+1}))$，累积到无穷步或者终止状态时，我们就得到了整个策略价值提升的不等式

策略迭代

• 策略迭代算法的过程如下：对当前的策略进行策略评估，得到其状态价值函数，然后根据该状态价值函数进行策略提升以得到一个更好的新策略，接着继续评估新策略、提升策略……直至最后收敛到最优策略
  

价值迭代算法

• 策略迭代中的策略评估需要进行很多轮才能收敛得到某一策略的状态函数，这需要很大的计算量，尤其是在状态和动作空间比较大的情况下

• 价值迭代算法，它可以被认为是一种策略评估只进行了一轮更新的策略迭代算法

• 需要注意的是，价值迭代中不存在显式的策略，只维护一个状态价值函数

• 价值迭代可以看成一种动态规划过程，它利用的是贝尔曼最优方程
  V ∗ ( s ) = max ⁡ a ∈ A { r ( s , a ) + γ ∑ s t + 1 ∈ S P ( s t + 1 ∣ s t , a t ) V ∗ ( s t + 1 ) } \begin{aligned} V^*(s) &= \max_{a \in A} \{r(s,a)+ \gamma \sum_{s_{t+1} \in S}P(s_{t+1}|s_t,a_t)V^*(s_{t+1})\} \end{aligned} V∗(s)​=a∈Amax​{r(s,a)+γst+1​∈S∑​P(st+1​∣st​,at​)V∗(st+1​)}​

• 将其写成迭代更新的方式
  V k + 1 ( s ) = max ⁡ a ∈ A { r ( s , a ) + γ ∑ s t + 1 ∈ S P ( s t + 1 ∣ s t , a t ) V k ( s t + 1 ) } \begin{aligned} V^{k+1}(s)=\max_{a \in A} \{r(s,a)+ \gamma \sum_{s_{t+1} \in S}P(s_{t+1}|s_t,a_t)V^k(s_{t+1})\} \end{aligned} Vk+1(s)=a∈Amax​{r(s,a)+γst+1​∈S∑​P(st+1​∣st​,at​)Vk(st+1​)}​

• 价值迭代按照以上更新方式进行, 等到$V^{k+1}$和$V^k$相同时，它就是贝尔曼最优方程的不动点，此时对应着最优状态价值函数$V^{\ast }(s)$

• 然后利用下式，从中恢复出最优策略即可
  π ( s ) = a r g max ⁡ a ∈ A { r ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V k ( s ′ ) } \begin{aligned} \pi(s) = arg \max_{a \in A} \{ r(s,a) + \gamma \sum_{s'\in S}P(s'|s,a)V^k(s') \} \end{aligned} π(s)=arga∈Amax​{r(s,a)+γs′∈S∑​P(s′∣s,a)Vk(s′)}​
  

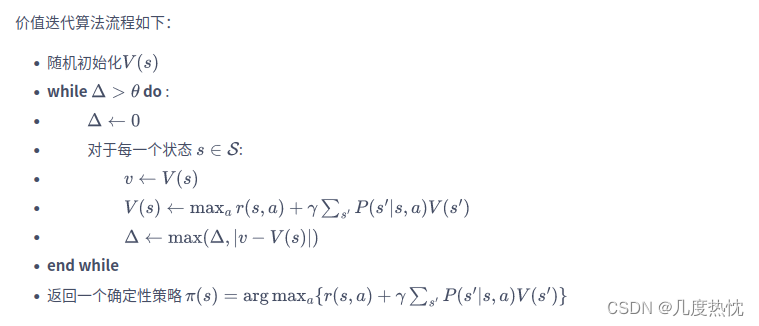
• 解决同样的训练任务，价值迭代中的循环次数远少于策略迭代

---

未运行书中的代码，下次补上，在此标记

---

收敛性证明

策略迭代

• 根据策略提升定理，更新后的策略的价值函数满足单调性，即$V_{\pi }^k\le V_{\pi }^{k+1}$
• 只要所有可能的策略个数是有限的，策略迭代就能收敛到最优策略
• 假设 MDP 的状态空间大小为$|S|$，动作空间大小为$|A|$，此时所有可能的策略个数为$|A{|}^{|S|}$，是有限个，所以策略迭代能够在有限步找到其中的最优策略

策略个数为什么是$|A{|}^{|S|}$个？
策略$\pi (a|s)$，由于每个状态都可以对应多个动作（尽管在实际的策略中，每个状态通常只对应一个动作），因此对于每个状态，都有$|A|$种可能的动作选择，对于第一个状态，我们有$|A|$种选择；对于第二个状态，我们同样有$|A|$种选择；对于第三个状态，还是$|A|$种选择，以此类推。对于所有的$|S|$个状态，每个状态都有$|A|$种可能的动作选择
$策略个数=|A|\mid \times |A|\times |A|\times \dots \times |A|\times |A|=|A{|}^{|S|}$

这里没看懂

价值迭代

• 价值迭代的更新公式为：

V k + 1 ( s ) = max ⁡ a ∈ A { r ( s , a ) + γ ∑ s t + 1 ∈ S P ( s t + 1 ∣ s t , a t ) V k ( s t + 1 ) } \begin{aligned} V^{k+1}(s)=\max_{a \in A} \{r(s,a)+ \gamma \sum_{s_{t+1} \in S}P(s_{t+1}|s_t,a_t)V^k(s_{t+1})\} \end{aligned} Vk+1(s)=a∈Amax​{r(s,a)+γst+1​∈S∑​P(st+1​∣st​,at​)Vk(st+1​)}​

• 定义贝尔曼最优算子$\mathcal{T}$
  V k + 1 ( s ) = T V k ( s ) = max ⁡ a ∈ A { r ( s , a ) + γ ∑ s t + 1 ∈ S P ( s t + 1 ∣ s t , a t ) V k ( s t + 1 ) } \begin{aligned} V^{k+1}(s)=\mathcal{T} V^{k}(s)=\max_{a \in A} \{r(s,a)+ \gamma \sum_{s_{t+1} \in S}P(s_{t+1}|s_t,a_t)V^k(s_{t+1})\} \end{aligned} Vk+1(s)=TVk(s)=a∈Amax​{r(s,a)+γst+1​∈S∑​P(st+1​∣st​,at​)Vk(st+1​)}​

• 引入压缩算子$O$（contraction operator）:若$O$是一个算子且满足$\Vert OV-O{V}^{\prime }{\Vert }_q\le \Vert V-V^{\prime }{\Vert }_q$，称$O$是一个压缩算子，其中$\Vert x{\Vert }_q$表示$x$的$L_q$范数

• 无穷范数：$\Vert x{\Vert }_{\infty }={\max }_i|x_i|$

• 证明：当$\gamma \le 1$时，贝尔曼最优算子$\mathcal{T}$是一个$\gamma$-压缩算子,注意是无穷范数哦，公式参考上面
  ∥ T V − T V ′ ∥ ∞ = max ⁡ s ∈ S ∣ max ⁡ a ∈ A { r ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V ( s ′ ) } − max ⁡ a ′ ∈ A { r ( s , a ′ ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ′ ) V ′ ( s ′ ) } ∣ ≤ max ⁡ s , a ∣ r ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V ( s ′ ) − r ( s , a ) − γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V ′ ( s ′ ) ∣ = γ max ⁡ s , a ∣ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) ( V ( s ′ ) − V ′ ( s ′ ) ) ∣ ≤ γ max ⁡ s , a ∑ s ′ ∈ S P ( s ′ ∣ s , a ) max ⁡ s ′ ∣ V ( s ′ ) − V ′ ( s ′ ) ∣ = γ ∥ V − V ′ ∥ ∞ \begin{aligned} \lVert \mathcal{T}V - \mathcal{T}V' \rVert_{\infty} &=\max_{s \in S} \lvert\max_{a \in A} \{r(s,a)+ \gamma \sum_{s' \in S}P(s'|s,a)V(s')\}-\max_{a' \in A} \{r(s,a')+\gamma \sum_{s' \in S}P(s'|s,a')V'(s') \} \rvert \\ &\le \max_{s,a} \lvert r(s,a) + \gamma \sum_{s' \in S}P(s'|s,a)V(s') -r(s,a)- \gamma \sum_{s' \in S}P(s'|s,a)V'(s') \rvert \\ &=\gamma\max_{s,a} \lvert \sum_{s' \in S}P(s'|s,a)(V(s') -V'(s')) \rvert \\ &\le \gamma\max_{s,a} \sum_{s' \in S}P(s'|s,a) \max_{s'} \lvert V(s') -V'(s') \rvert \\ &= \gamma \lVert V - V' \rVert_{\infty} \end{aligned} ∥TV−TV′∥∞​​=s∈Smax​∣a∈Amax​{r(s,a)+γs′∈S∑​P(s′∣s,a)V(s′)}−a′∈Amax​{r(s,a′)+γs′∈S∑​P(s′∣s,a′)V′(s′)}∣≤s,amax​∣r(s,a)+γs′∈S∑​P(s′∣s,a)V(s′)−r(s,a)−γs′∈S∑​P(s′∣s,a)V′(s′)∣=γs,amax​∣s′∈S∑​P(s′∣s,a)(V(s′)−V′(s′))∣≤γs,amax​s′∈S∑​P(s′∣s,a)s′max​∣V(s′)−V′(s′)∣=γ∥V−V′∥∞​​

推的很好，没看懂，之后再理解吧

• 设$V^{\prime }$为最优价值函数$V^{\ast }$,则有
  $\Vert V^{k+1}-V^{\ast }{\Vert }_{\infty }=\Vert \mathcal{T}{V}^k-\mathcal{T}{V}^{\ast }{\Vert }_{\infty }\le \gamma \Vert V^k-V^{\ast }{\Vert }_{\infty }\le \dots \le {\gamma }^{k+1}\Vert V^0-V^{\ast }{\Vert }_{\infty }$

• 在$\gamma \le 1$的情况下，随着迭代次数$k$越来越大，$V^k$会越来越接近$V^{\ast }$
  $\Vert V^{k+1}-V^{\ast }{\Vert }_{\infty }\le {\gamma }^{k+1}\Vert V^0-V^{\ast }{\Vert }_{\infty }$

• 每次迭代，误差都会乘以$\gamma$的$k+1$ 次方。由于$\gamma$小于1，随着$k$ 的增加，$\gamma$的$k+1$ 次方会趋向于0。因此，随着迭代次数的增加，$V^{k+1}-V^{\ast }$趋于0,误差不断减小

• 即${\lim }_{k\to \infty }{V}^k=V^{\ast }$。至此，价值迭代的收敛性得到证明

总结

• 两个经典的动态规划算法：策略迭代算法和价值迭代算法，它们都能用于求解最优价值和最优策略
• 动态规划的主要思想是利用贝尔曼方程对所有状态进行更新。需要注意的是，在利用贝尔曼方程进行状态更新时，需要已知马尔可夫决策过程中的奖励函数和状态转移函数

原文地址：https://blog.csdn.net/Ever_____/article/details/137567324

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！